P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:

(i) DP : PL = DC : BL.

(ii) DL : DP = AL : DC.

Parallelogram ABCD is shown in the figure below:

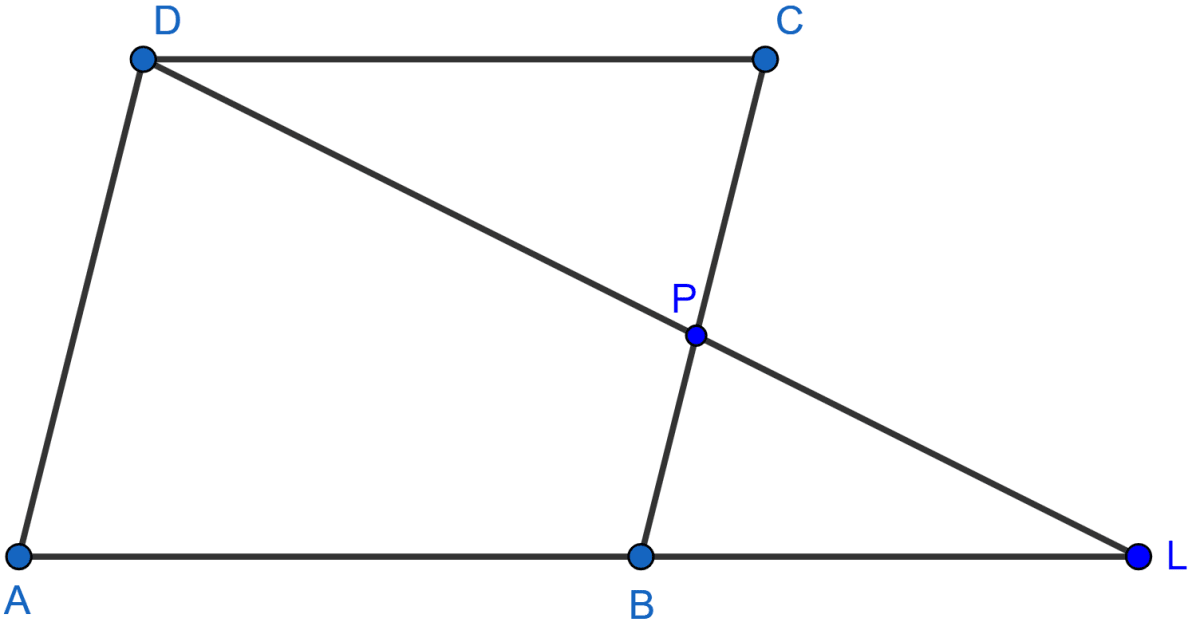
(i) In ∆DPC and ∆BPL, we have

∠DPC = ∠BPL [Vertically opposite angles area equal]

∠DCP = ∠PBL [Alternate angles (as AB || DC) are equal]

∴ ∆DPC ~ ∆BPL [By A.A.]

Since, corresponding sides of similar triangles are proportional.

$\therefore \dfrac{DP}{PL} = \dfrac{DC}{BL}$.

i.e., DP : PL = DC : BL.

Hence, proved that DP : PL = DC : BL.

(ii) From part (i) we get,

$\Rightarrow \dfrac{DP}{PL} = \dfrac{DC}{BL} \\[1em] \Rightarrow \dfrac{PL}{DP} = \dfrac{BL}{DC} \\[1em] \Rightarrow \dfrac{PL}{DP} + 1 = \dfrac{BL}{DC} + 1 \\[1em] \Rightarrow \dfrac{PL + DP}{DP} = \dfrac{BL + DC}{DC} \\[1em] \Rightarrow \text{Since, AB = DC as ABCD is a || gm} \\[1em] \Rightarrow \dfrac{PL + DP}{DP} = \dfrac{BL + AB}{DC} \\[1em] \Rightarrow \dfrac{DL}{DP} = \dfrac{AL}{DC}.$

Hence, proved that DL : DP = AL : DC.