Mathematics
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
Similarity
19 Likes
Answer
ΔABC is shown in the figure below:
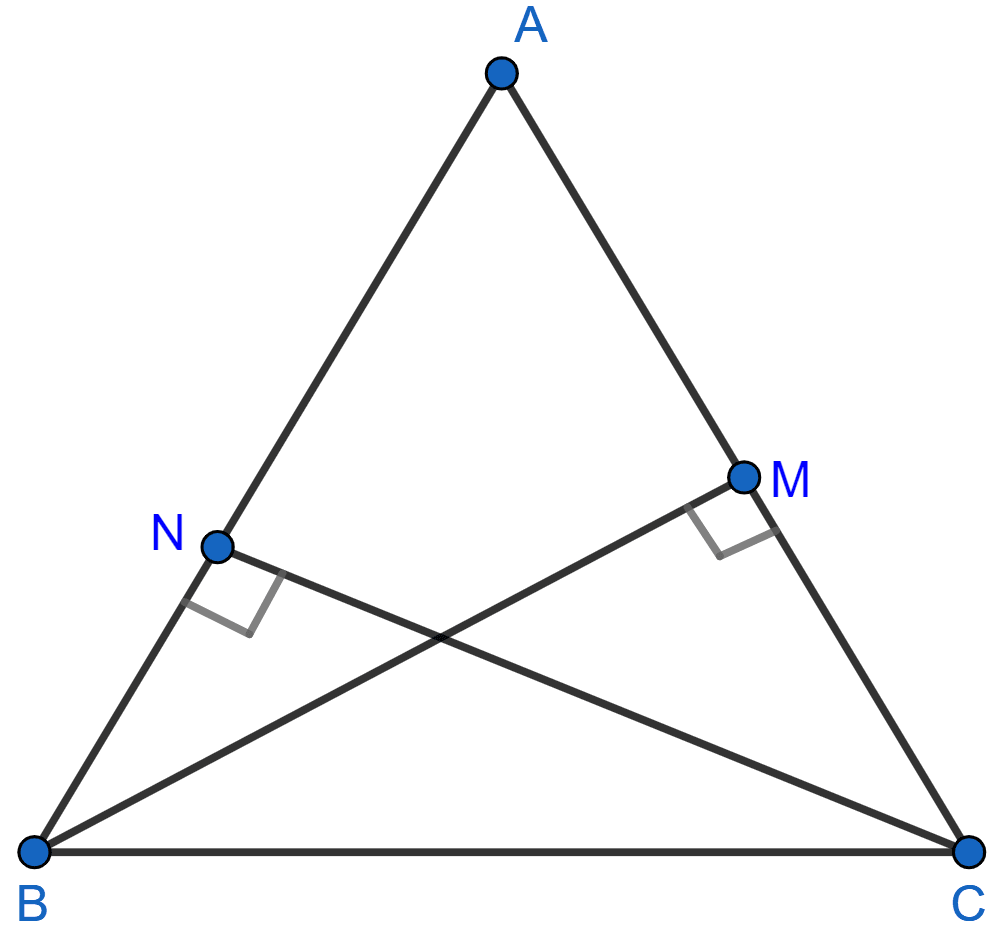
In ΔABM and ΔACN,
∠AMB = ∠ANC [Since, BM ⊥ AC and CN ⊥ AB]
∠BAM = ∠CAN [Common angle]
∴ ∆ABM ~ ∆ACN [By A.A.]
Since corresponding sides of similar triangles are proportional we have,
⇒
Hence, proved that .
Answered By
17 Likes
Related Questions
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP : PL = DC : BL.
(ii) DL : DP = AL : DC.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
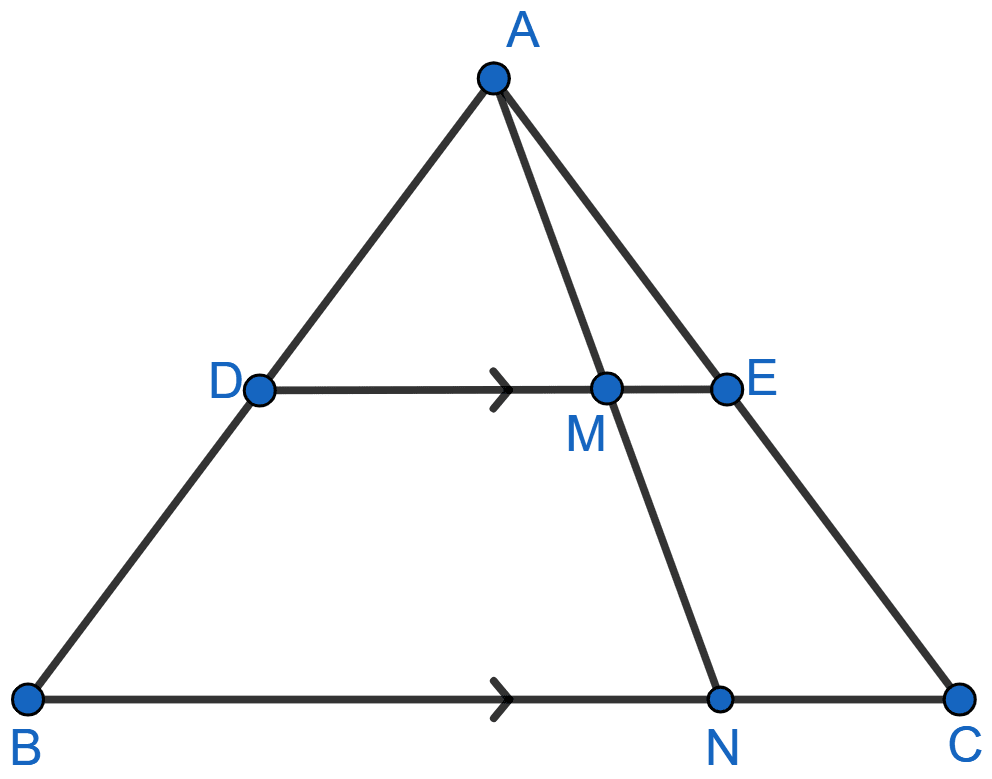
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.
In the given figure, AD = AE and AD2 = BD x EC. Prove that: triangles ABD and CAE are similar.