Mathematics
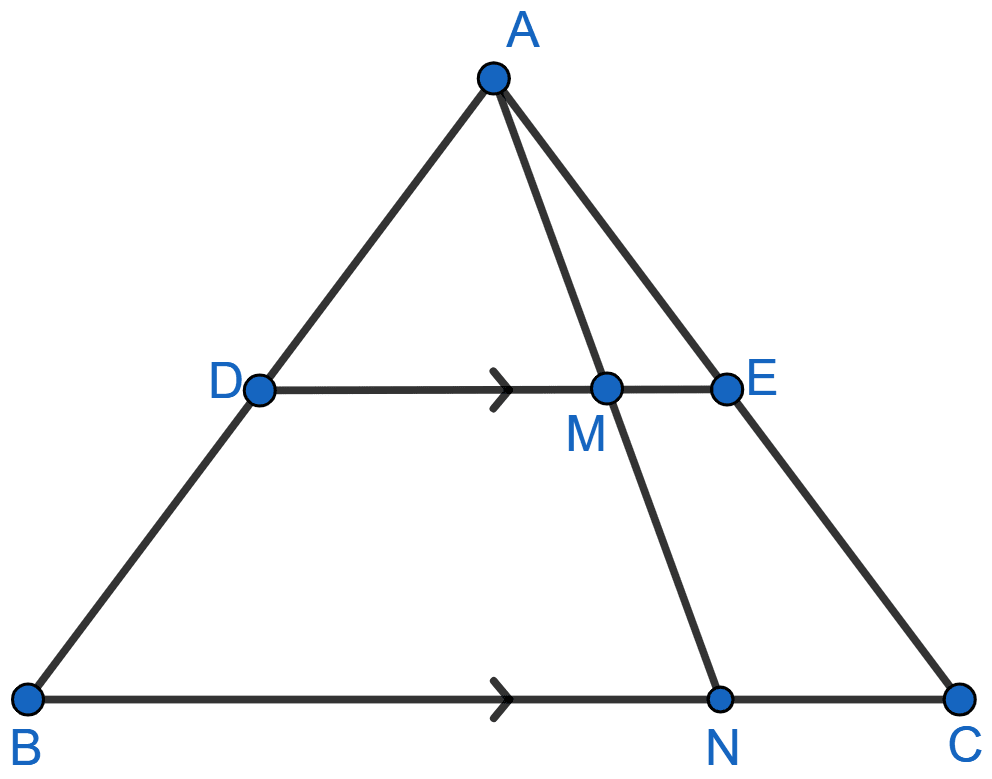
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.
Similarity
35 Likes
Answer
(i) In ΔAME and ΔANC,
⇒ ∠AME = ∠ANC [Since DE || BC so, ME || NC and AN is transversal]
⇒ ∠MAE = ∠NAC [Common angle]
∴ ∆AME ~ ∆ANC [By AA]
In ΔADM and ΔABN,
⇒ ∠ADM = ∠ABN [Since DE || BC so, DM || BN and AB is transversal]
⇒ ∠DAM = ∠BAN [Common angle]
∴ ∆ADM ~ ∆ABN [By AA]
In ΔADE and ΔABC,
⇒ ∠ADE = ∠ABC [Since DE || BC and AB is transversal]
⇒ ∠AED = ∠ACB [Since DE || BC and AC is transversal]
∴ ∆ADE ~ ∆ABC [By AA]
Hence, ∆ADM ~ ∆ABN, ∆AME ~ ∆ANC and ∆ADE ~ ∆ABC.
(ii) Since, ∆AME ~ ∆ANC
We know that,
Corresponding sides of similar triangles are proportional.
Since, ∆ADE ~ ∆ABC [Proved above]
We know that,
Corresponding sides of similar triangles are proportional.
……… (1)
Also, ∆ADM ~ ∆ABN [Proved above]
Hence, ME = 3.75 cm and DM = 15 cm.
Answered By
21 Likes
Related Questions
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
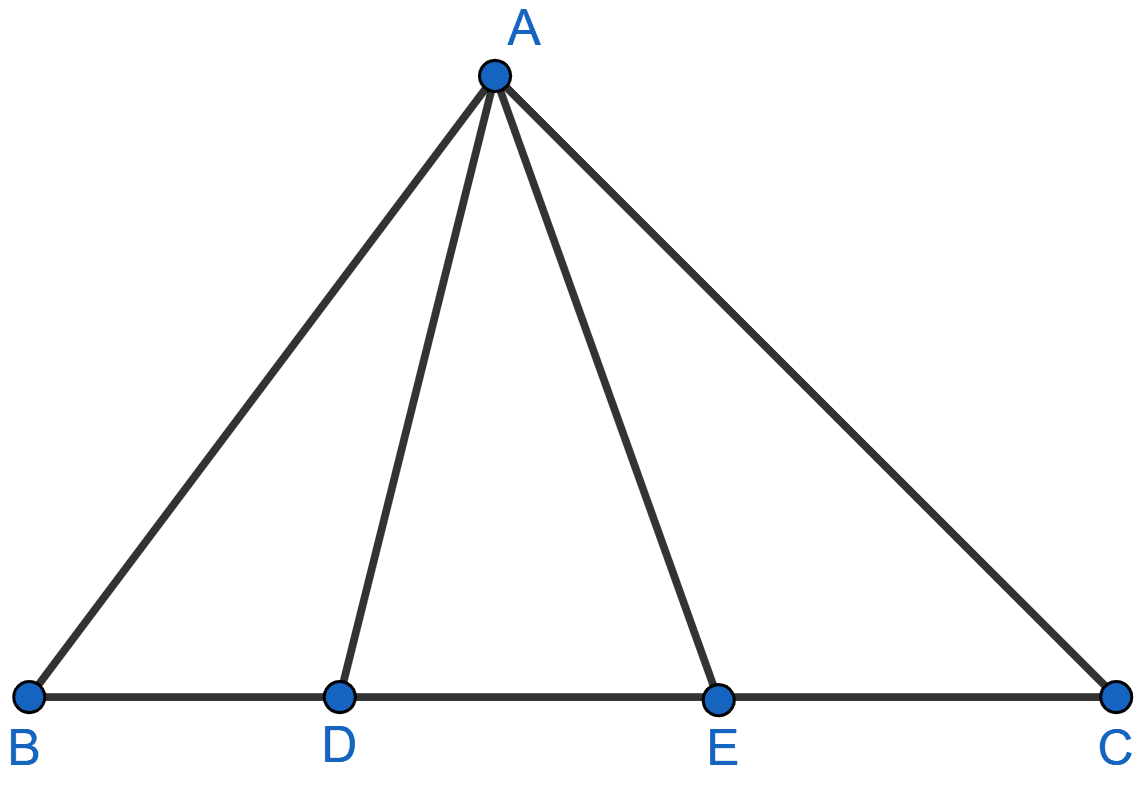
In the given figure, AD = AE and AD2 = BD x EC. Prove that: triangles ABD and CAE are similar.
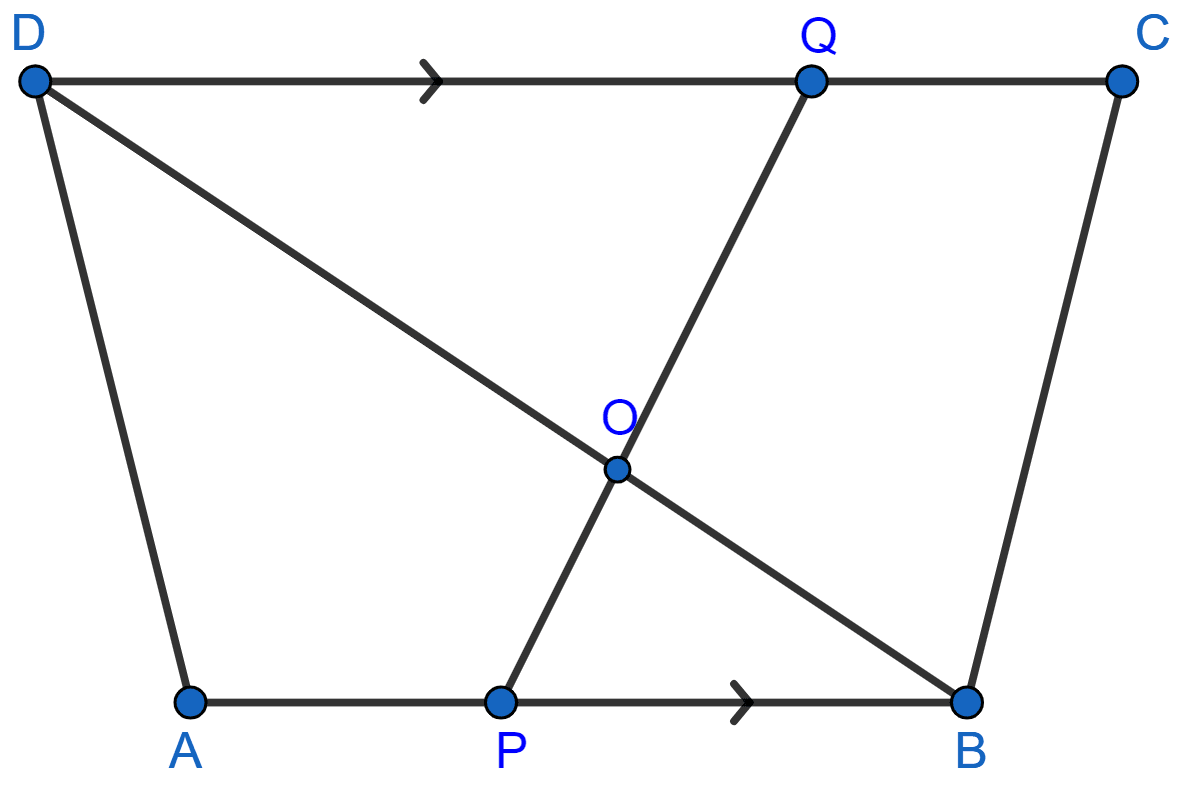
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.