Mathematics
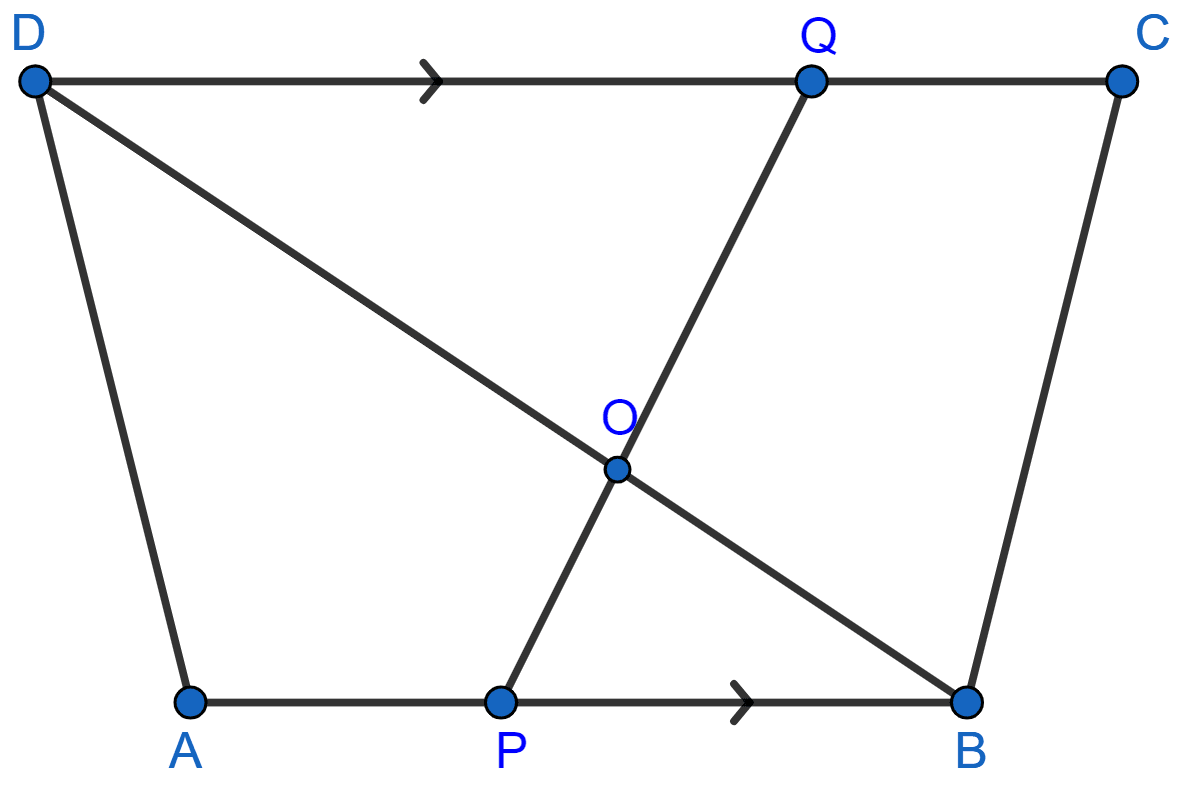
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
Similarity
31 Likes
Answer
In ΔDOQ and ΔBOP,
As AB || DC so, PB || DQ and BD is transversal.
∴ ∠QDO = ∠PBO [Alternate angles]
∠DOQ = ∠BOP [Vertically opposite angles are equal]
Hence, ∆DOQ ~ ∆BOP [By AA]
Since, corresponding sides of similar triangles are proportional we have :
Hence, BP x DO = 48 cm2.
Answered By
20 Likes
Related Questions
The value of x is :
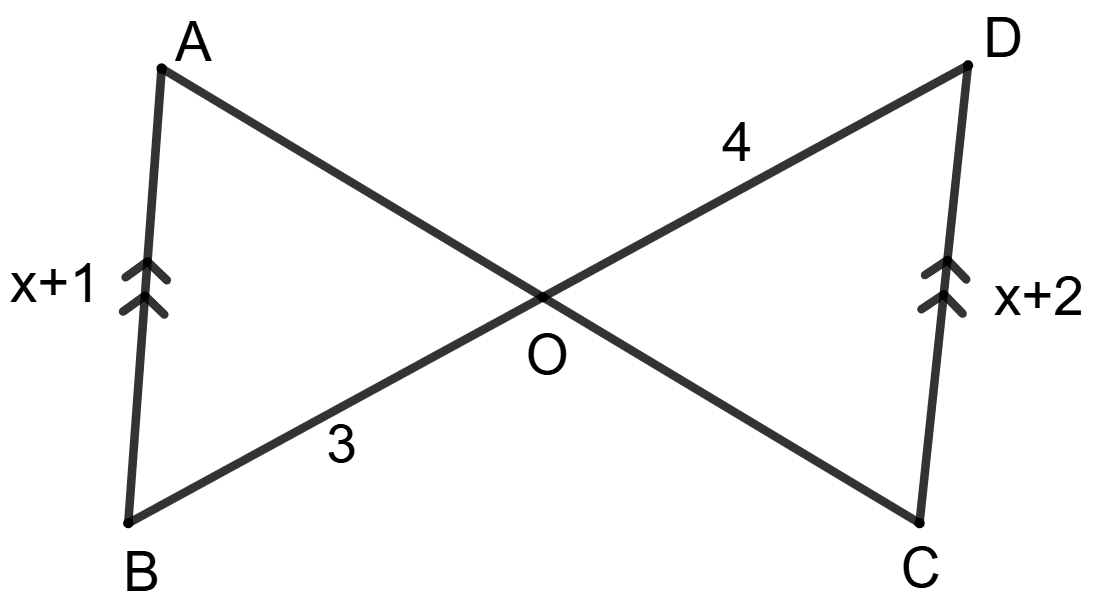
2
3
1
none of these
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:
(i) ∆APC and ∆BPD are similar.
(ii) If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.

In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
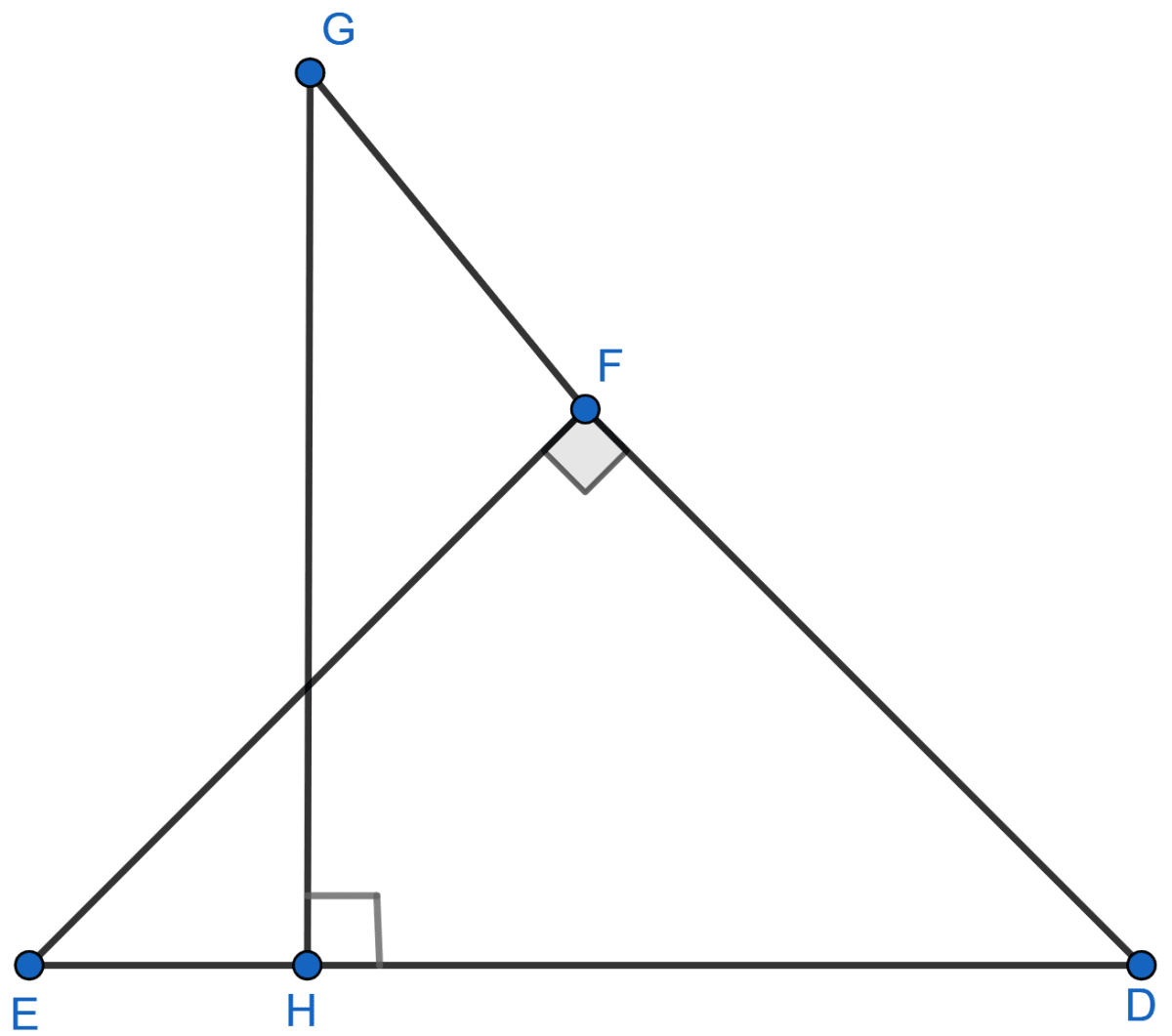
Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.