Mathematics
In △ABC, AB = AC = x, BC = 10 cm and the area of △ABC is 60 cm2. Find x.
Pythagoras Theorem
Answer
Let AD be the altitude. In isosceles triangle, the altitude to base bisects the base.
∴ BD = CD = 5 cm.
From figure,
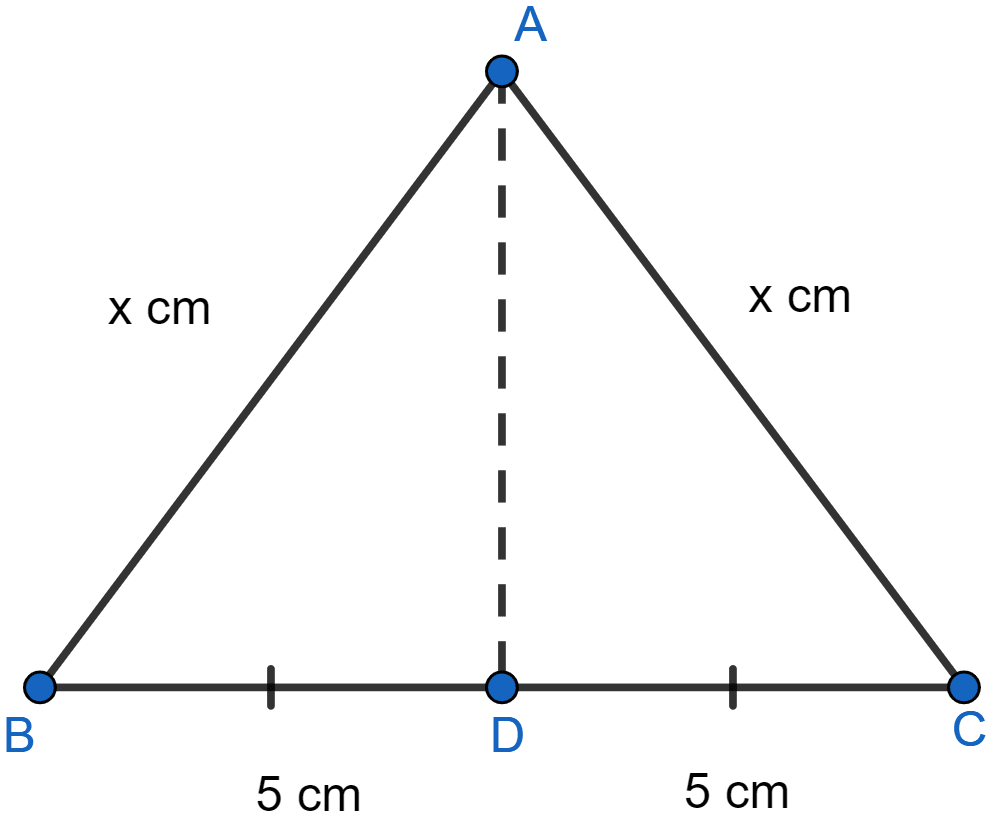
In right triangle ABD,
AB2 = AD2 + BD2
x2 = AD2 + 52
AD2 = x2 - 25.
AD =
Hence, x = 13 cm.
Answered By
Related Questions
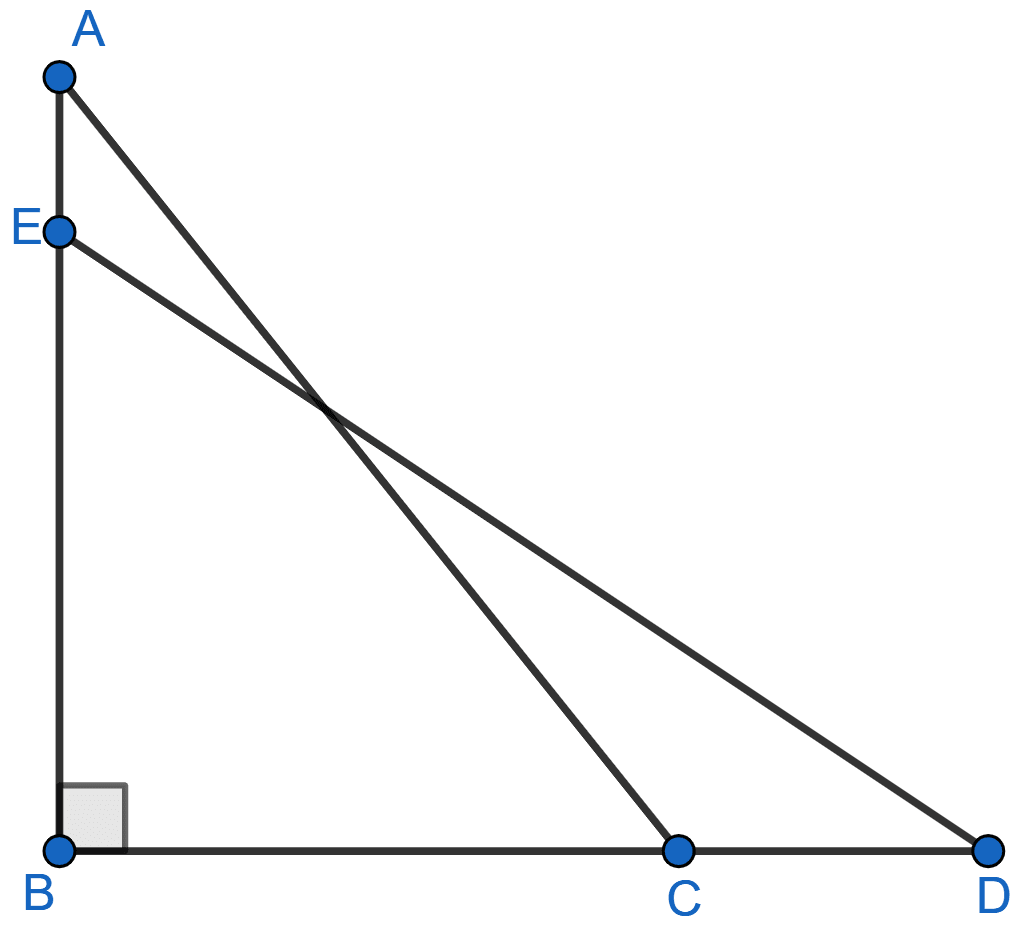
In figure given below, BC = 5 cm, ∠B = 90°, AB = 5AE, CD = 2AE and AC = ED. Calculate the lengths of EA, CD, AB and AC.
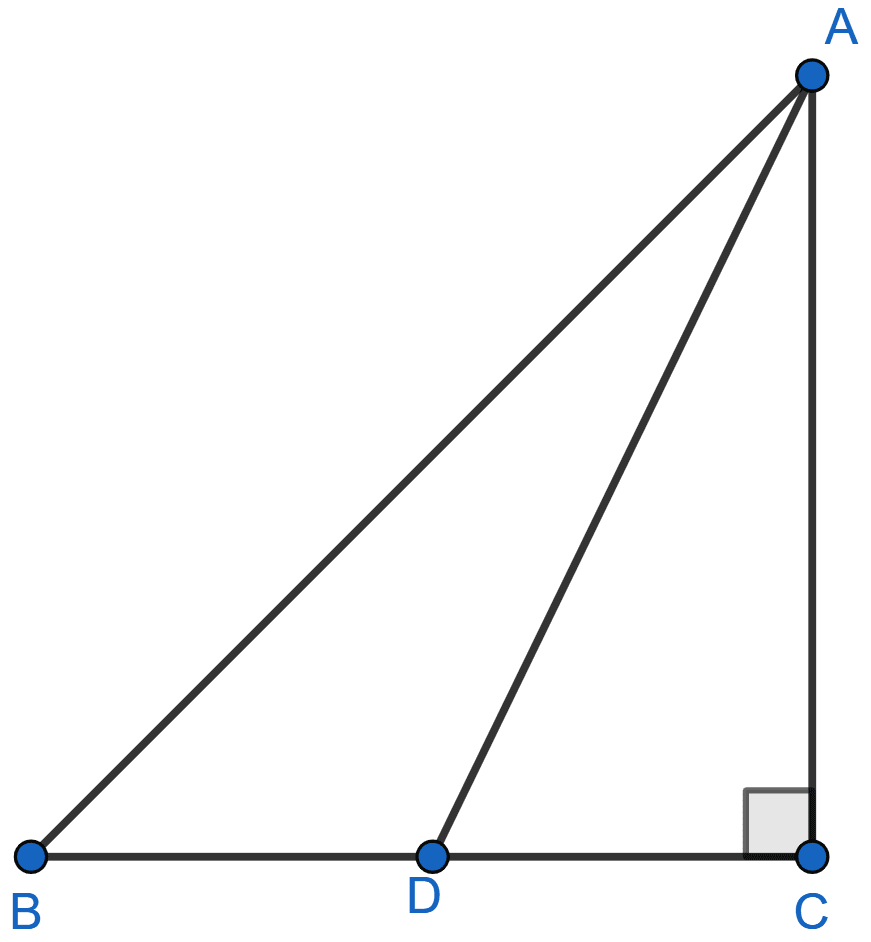
In figure given below, ABC is a right triangle right angled at C. If D is mid-point of BC, prove that AB2 = 4AD2 - 3AC2.
In rhombus if diagonals are 30 cm and 40 cm, find its perimeter.
In figure given below, AB || DC, BC = AD = 13 cm, AB = 22 cm and DC = 12 cm. Calculate the height of the trapezium ABCD.
