Mathematics
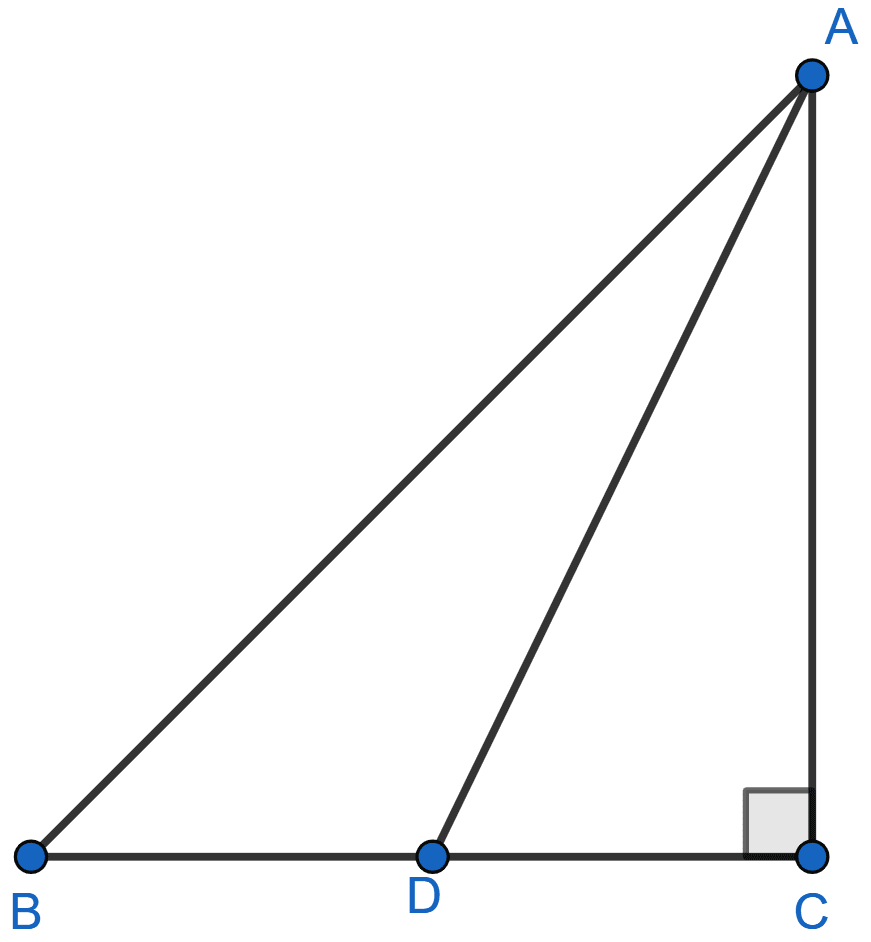
In figure given below, ABC is a right triangle right angled at C. If D is mid-point of BC, prove that AB2 = 4AD2 - 3AC2.
Pythagoras Theorem
81 Likes
Answer
Since, D is mid-point of BC so we get,
DC = .
ABC is a right triangle.
By pythagoras theorem,
⇒ AB2 = AC2 + BC2 …….(i)
ADC is a right triangle.
By pythagoras theorem,
⇒ AD2 = AC2 + DC2 …….(ii)
⇒ AC2 = AD2 - DC2
⇒ AC2 = AD2 -
⇒ AC2 = AD2 -
⇒ AC2 =
⇒ 4AC2 = 4AD2 - BC2
⇒ AC2 + 3AC2 = 4AD2 - BC2
⇒ AC2 + BC2 = 4AD2 - 3AC2
⇒ AB2 = 4AD2 - 3AC2 [….From (i)]
Hence, proved that AB2 = 4AD2 - 3AC2.
Answered By
55 Likes
Related Questions
In figure given below, ∠D = 90°, AB = 16 cm, BC = 12 cm and CA = 6 cm. Find CD.

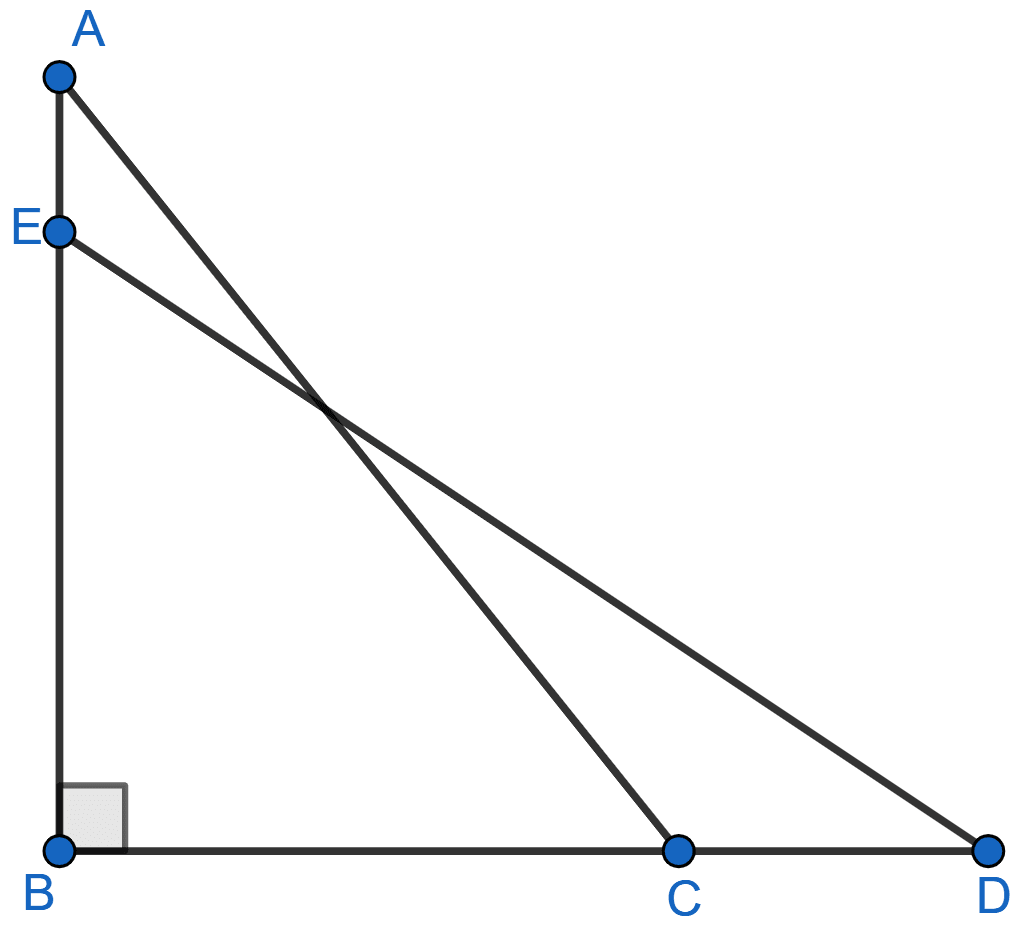
In figure given below, BC = 5 cm, ∠B = 90°, AB = 5AE, CD = 2AE and AC = ED. Calculate the lengths of EA, CD, AB and AC.
In △ABC, AB = AC = x, BC = 10 cm and the area of △ABC is 60 cm2. Find x.
In rhombus if diagonals are 30 cm and 40 cm, find its perimeter.