Mathematics
In rhombus if diagonals are 30 cm and 40 cm, find its perimeter.
Pythagoras Theorem
37 Likes
Answer
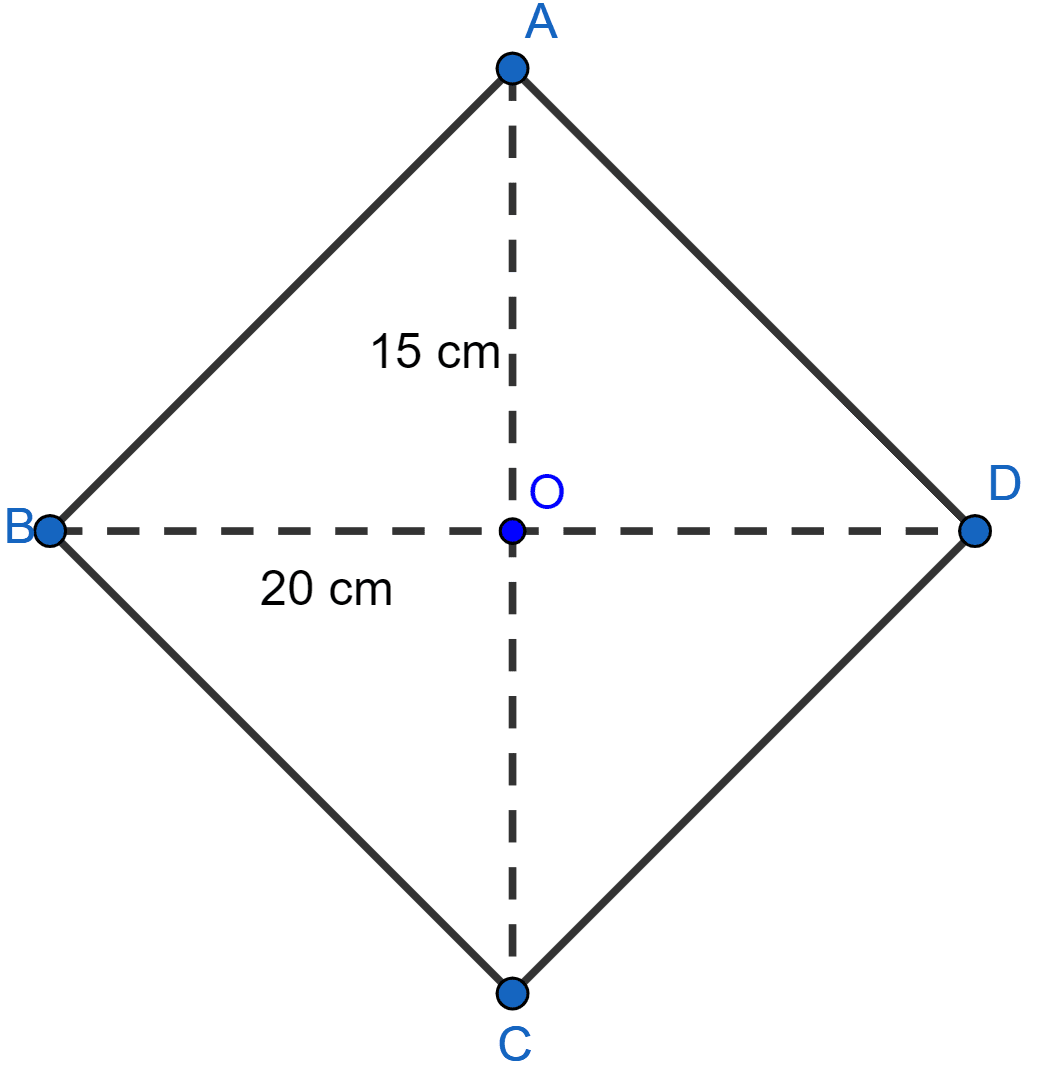
Let AC = 30 cm and BD = 40 cm.
We know that,
Diagonals of rhombus are perpendicular and bisect each other,
OB = = 20 cm and AO = AC = 15 cm.
In right triangle AOB,
By pythagoras theorem we get,
⇒ AB2 = AO2 + OB2
⇒ AB2 = 152 + 202
⇒ AB2 = 225 + 400
⇒ AB2 = 625
⇒ AB = 25 cm.
Hence, each side of rhombus is 25 cm as all sides of rhombus are equal.
Perimeter = 4(Side) = 100 cm.
Hence, perimeter of rhombus = 100 cm.
Answered By
31 Likes
Related Questions
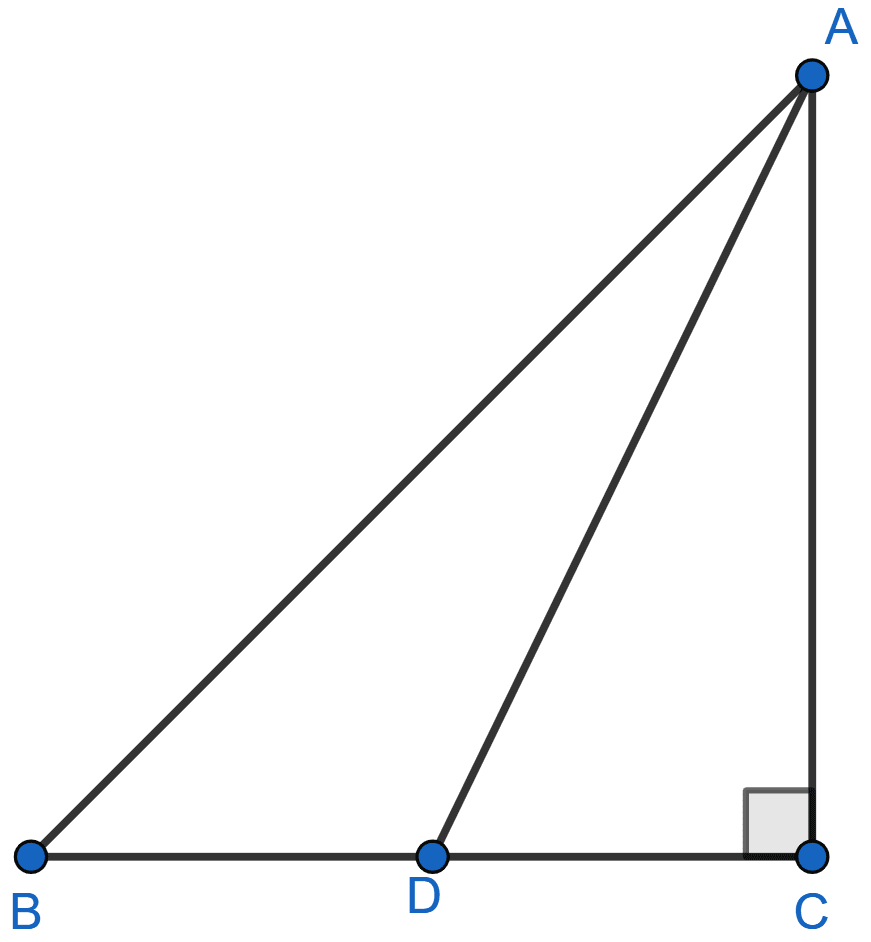
In figure given below, ABC is a right triangle right angled at C. If D is mid-point of BC, prove that AB2 = 4AD2 - 3AC2.
In △ABC, AB = AC = x, BC = 10 cm and the area of △ABC is 60 cm2. Find x.
In figure given below, AB || DC, BC = AD = 13 cm, AB = 22 cm and DC = 12 cm. Calculate the height of the trapezium ABCD.

In figure given below, AB || DC, ∠A = 90°, DC = 7 cm, AB = 17 cm and AC = 25 cm. Calculate BC.
