Mathematics
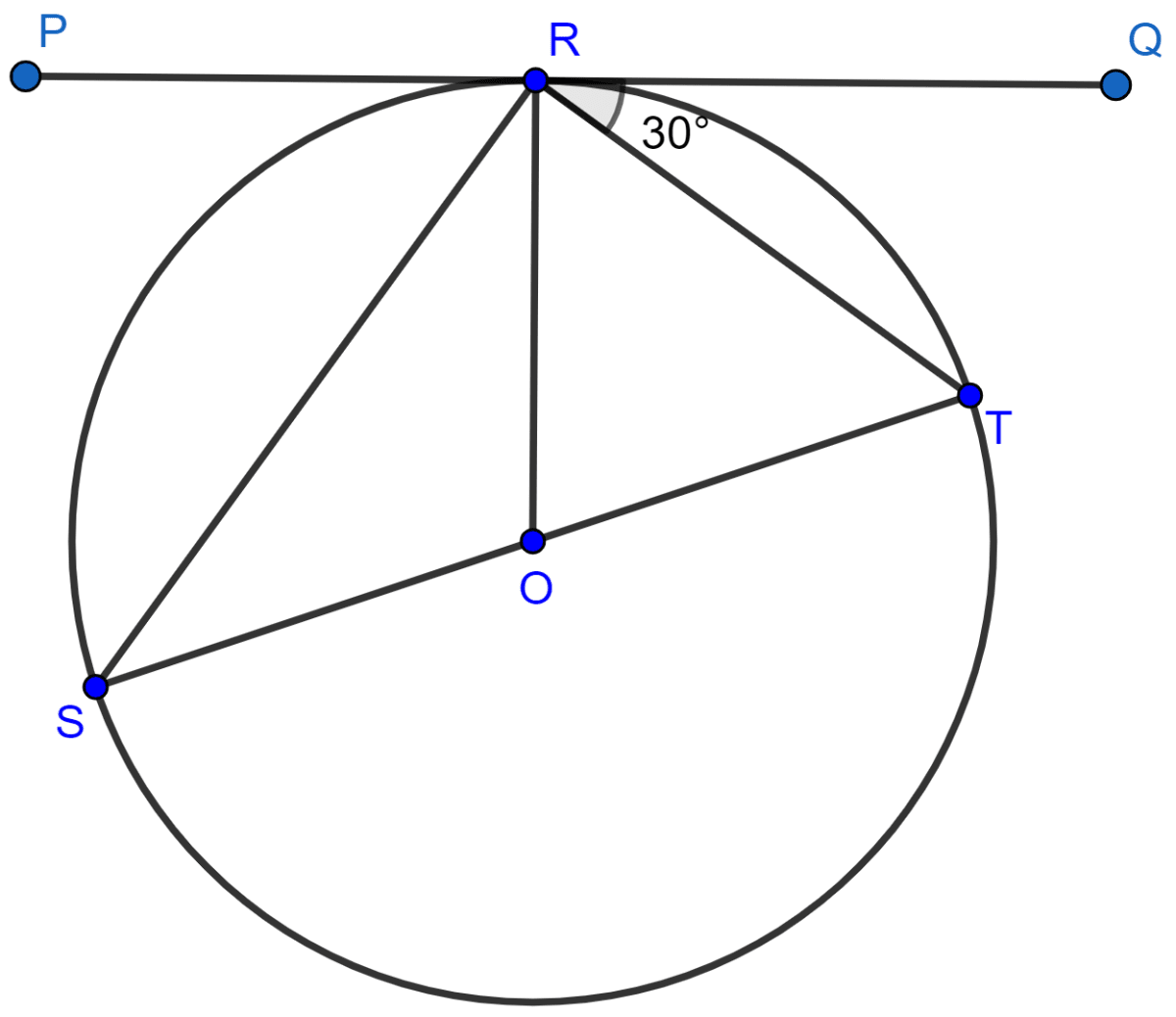
If PQ is a tangent to the circle at R; calculate :
(i) ∠PRS,
(ii) ∠ROT.
Given, O is the center of the circle and angle TRQ = 30°.
Circles
7 Likes
Answer
(i) Since, ST passes through O, so ST is the diameter of the circle.
We know that,
Angle in a semi-circle is a right angle.
∴ ∠SRT = 90°.
Since, PQ is a straight line.
∴ ∠PRS + ∠SRT + ∠TRQ = 180°
⇒ ∠PRS + 90° + 30° = 180°
⇒ ∠PRS + 120° = 180°
⇒ ∠PRS = 180° - 120°
⇒ ∠PRS = 60°.
Hence, ∠PRS = 60°.
(ii) We know that,
The angle between a tangent and chord through the point of contact is equal to an angle in the alternate segment.
∠TSR = ∠TRQ = 30°.
Since, angle subtended by a segment at the center is double the angle suspended at the circumference.
∠ROT = 2∠TSR = 2 × 30° = 60°.
Hence, ∠ROT = 60°.
Answered By
6 Likes
Related Questions
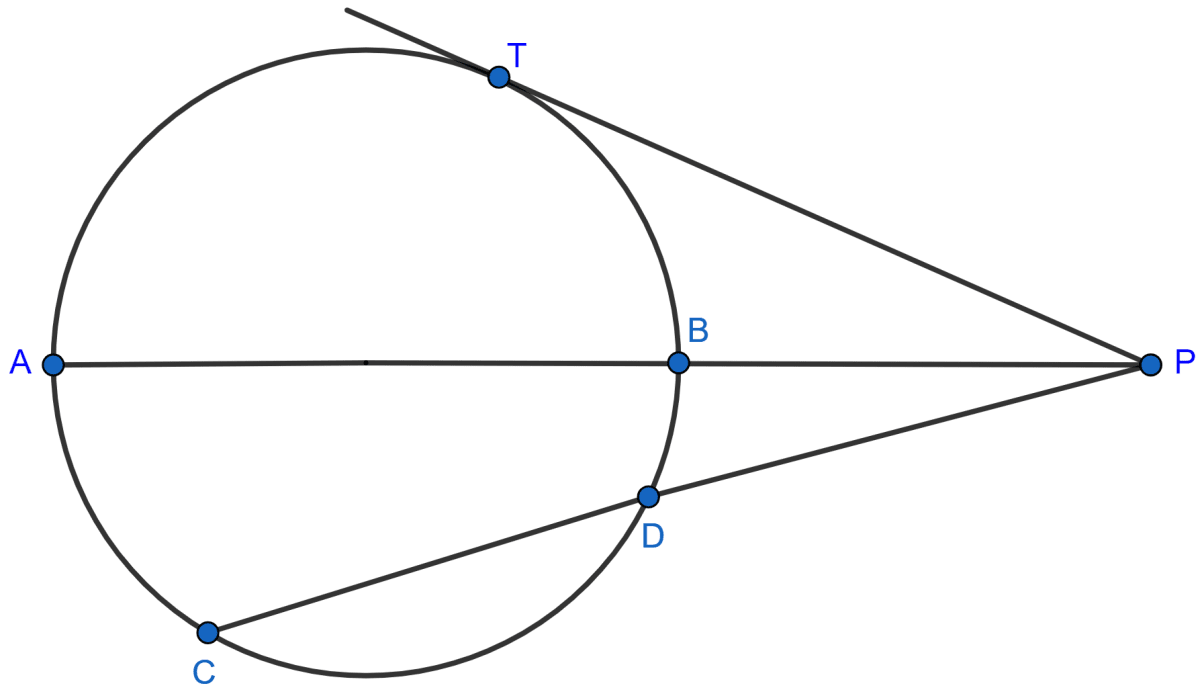
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find :
(i) AB
(ii) the length of tangent PT.
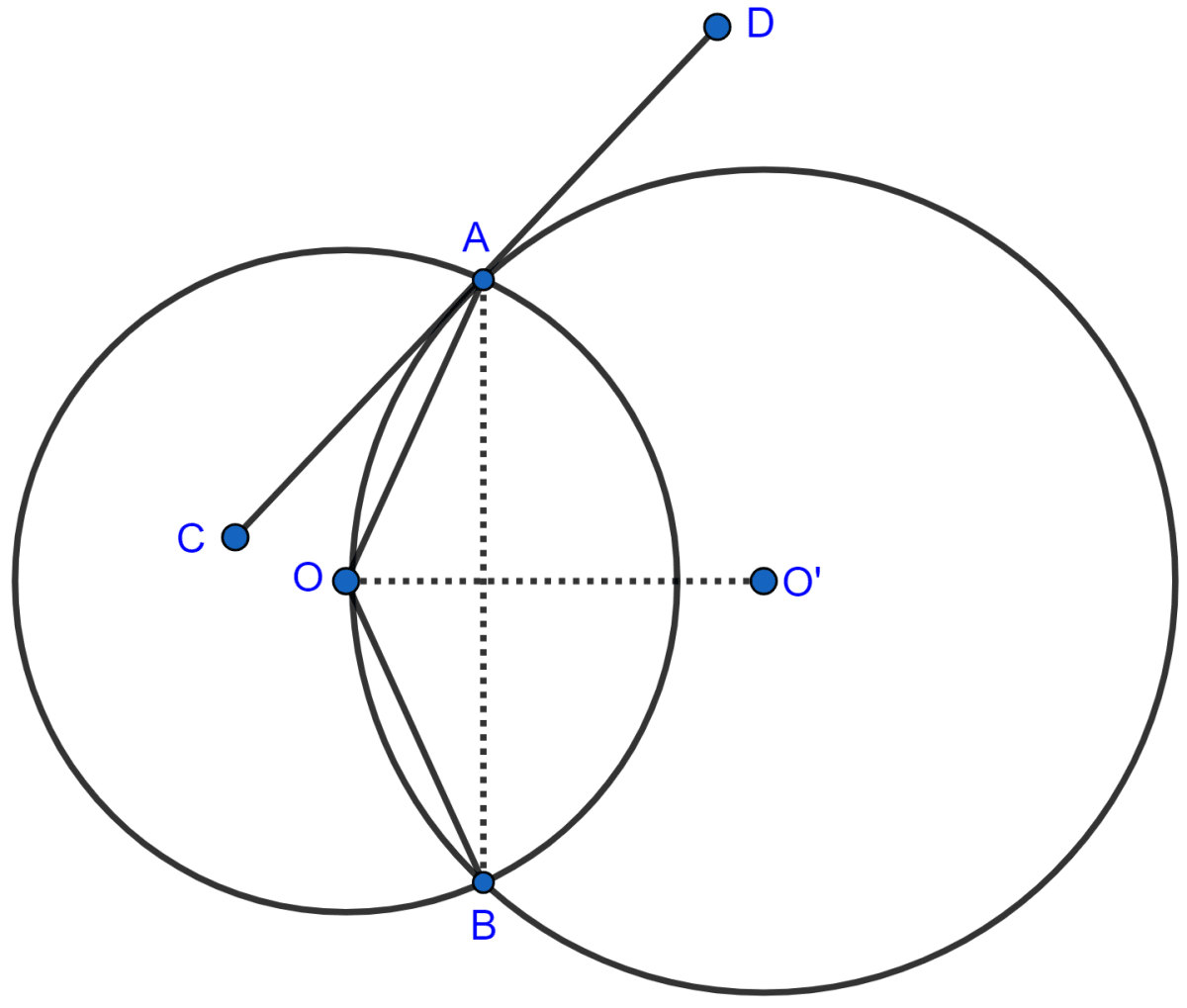
Two circles with centers O and O' are drawn to intersect each other at points A and B. Center O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with center O' at A. Prove that OA bisects angle BAC.
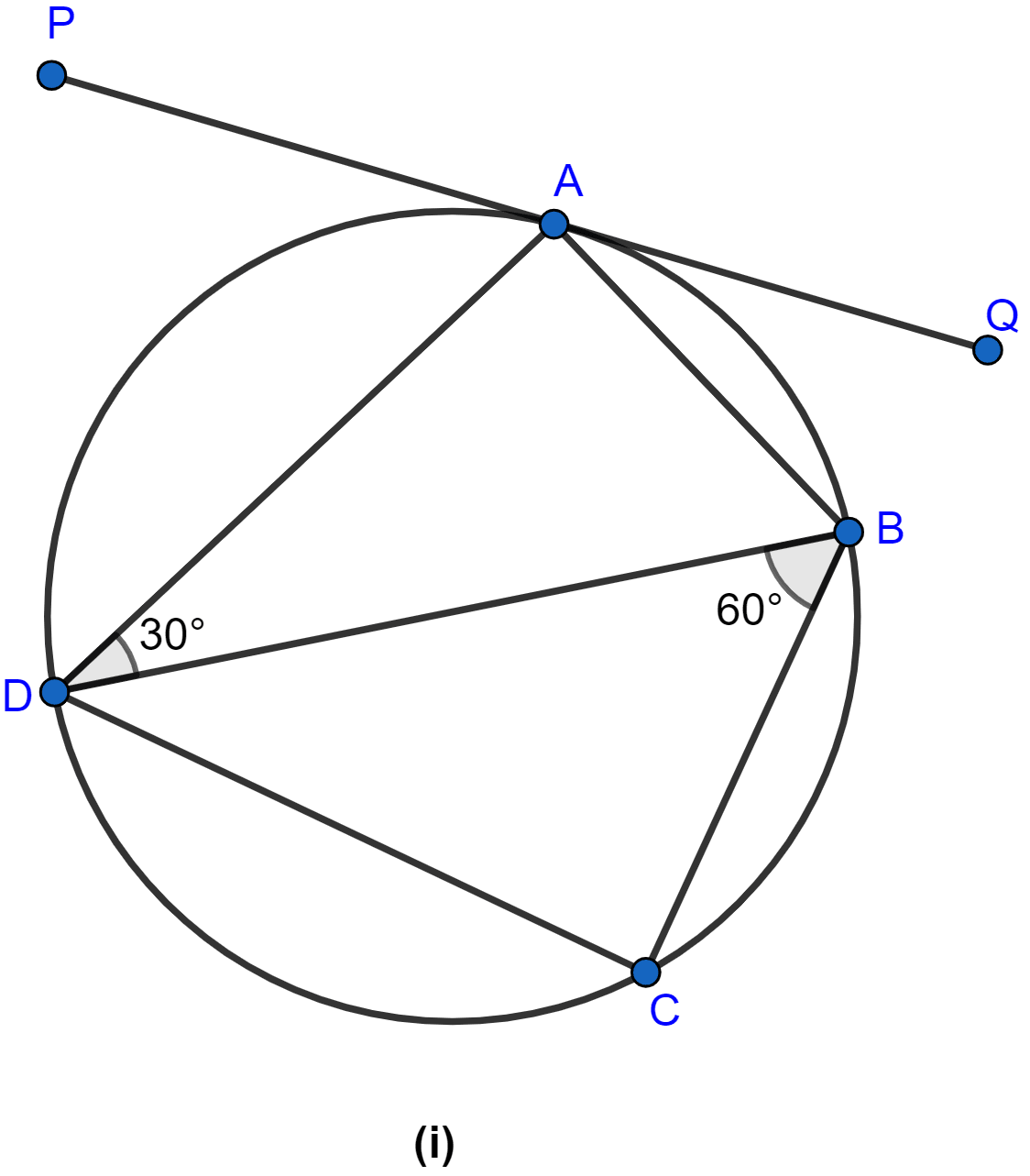
In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB.
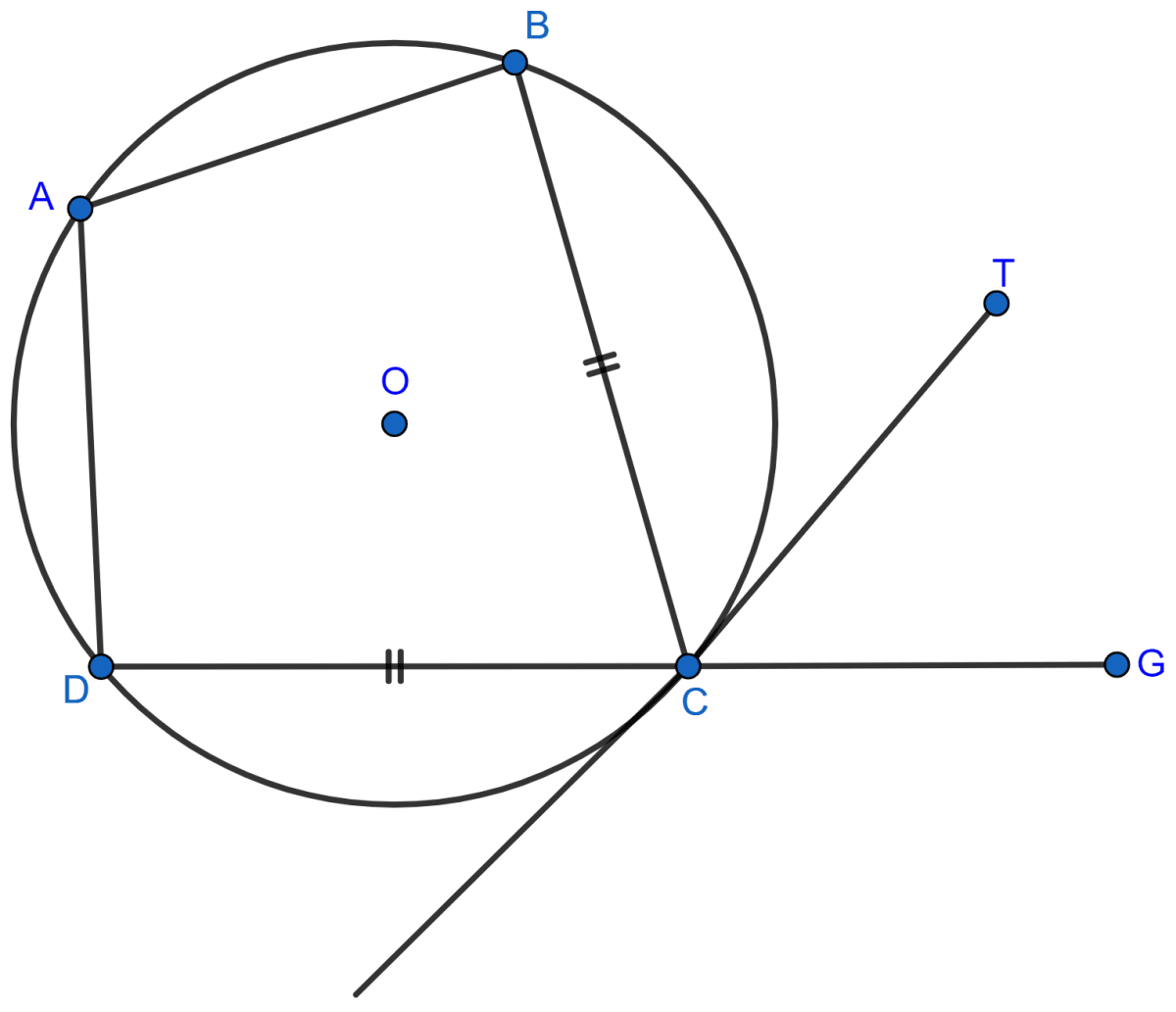
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the center of the circle, find :
(i) angle BCT
(ii) angle DOC