ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.

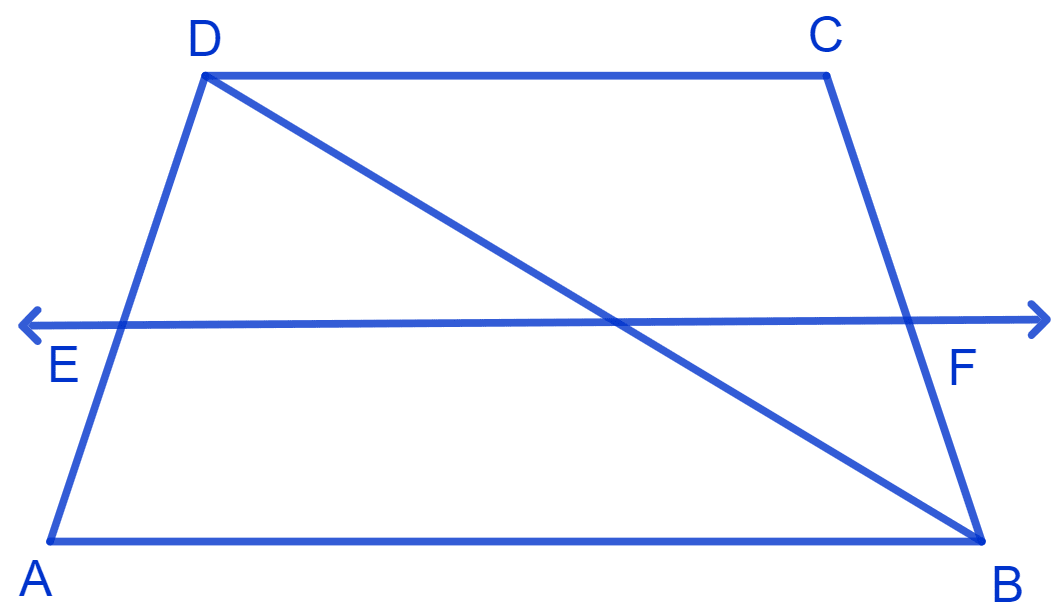
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F see Fig. Show that F is the mid-point of BC.

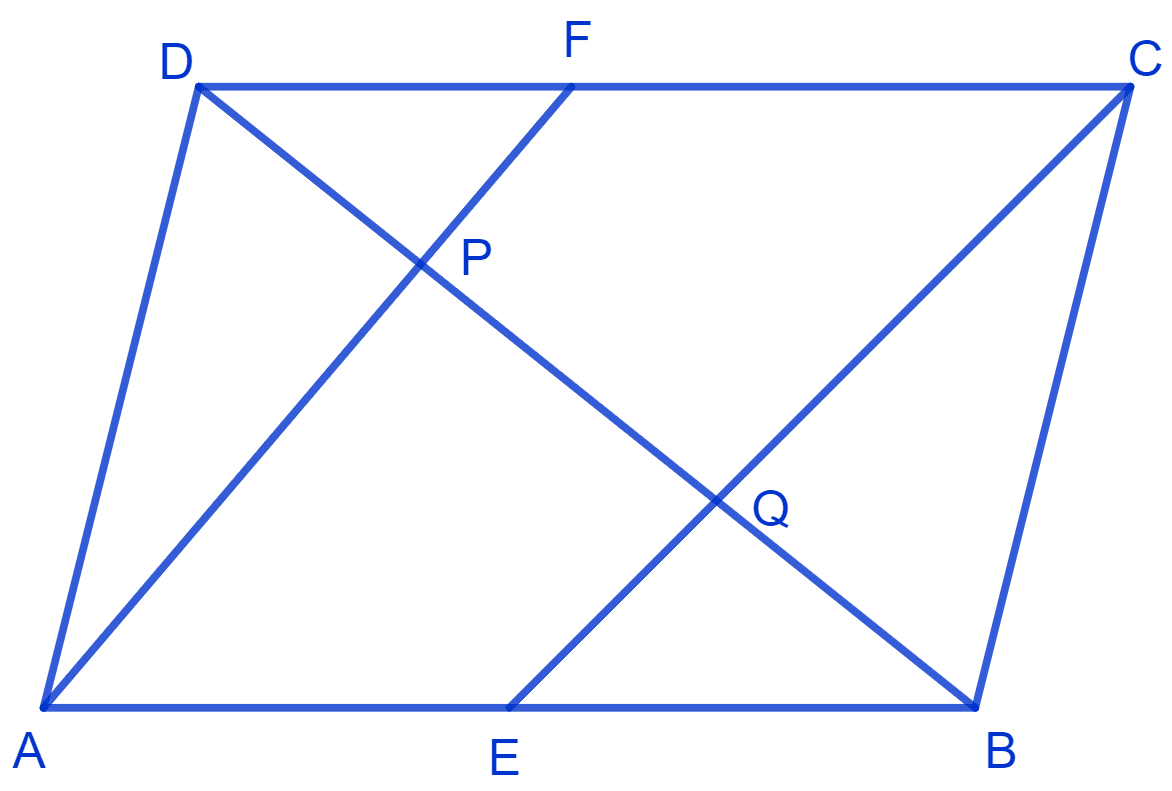
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively see Fig. Show that the line segments AF and EC trisect the diagonal BD.