Mathematics
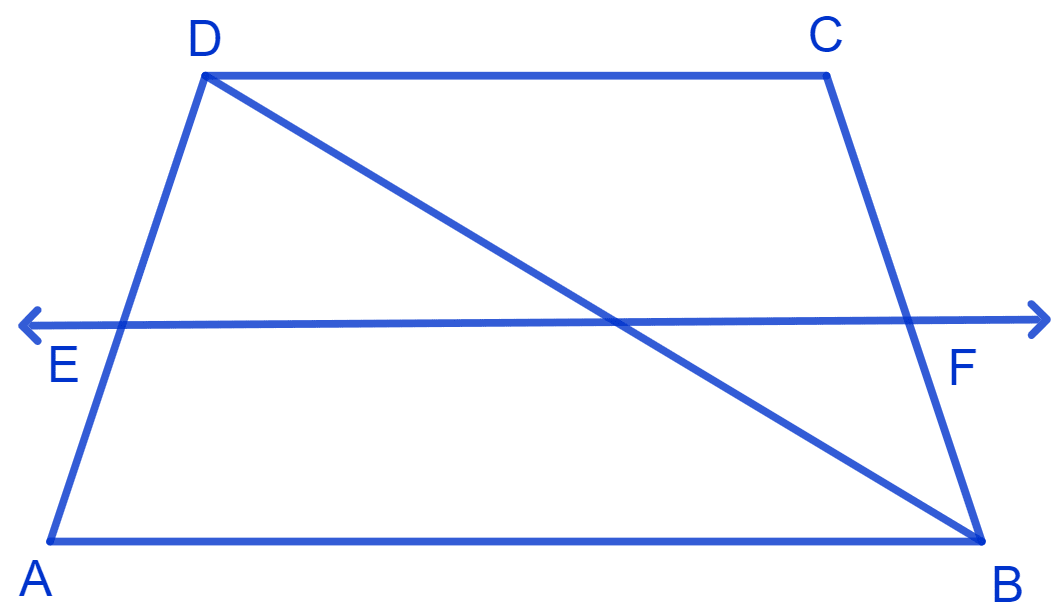
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F see Fig. Show that F is the mid-point of BC.
Rectilinear Figures
7 Likes
Answer
Given :
ABCD is a trapezium, where AB || DC, E is the mid-point of AD and EF || AB.
By converse of mid-point theorem,
A line drawn through the mid-point of any side of a triangle and parallel to another side bisects the third side.
Let EF intersect BD at point G.
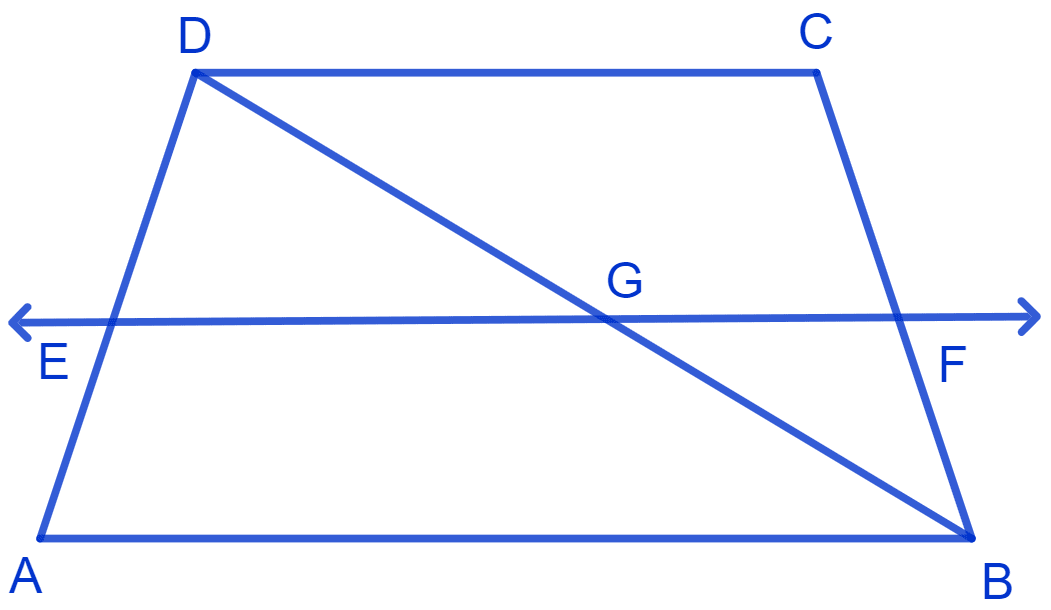
In trapezium ABCD,
EF || AB and E is the mid-point of AD.
By converse of mid-point theorem,
G is the mid-point of DB
As, EF || AB and AB || CD,
EF || CD (Two lines parallel to the same line are parallel to each other)
In Δ BCD,
GF || CD and G is the mid-point of line BD.
By using the converse of mid-point theorem, F is the mid-point of BC.
Hence, proved that F is the mid-point of BC.
Answered By
5 Likes
Related Questions
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively see Fig. Show that the line segments AF and EC trisect the diagonal BD.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA =