Mathematics
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Rectilinear Figures
6 Likes
Answer
We know that,
The diagonals of a rectangle are equal.
⇒ BD = AC = x (let)

In △ ABC,
P and Q are the mid-points of AB and BC respectively.
By mid-point theorem,
⇒ PQ || AC and PQ = ….(1)
In △ ADC,
S and R are the mid-points of AD and CD respectively.
SR || AC and SR = …..(2)
From equation (1) and (2), we get :
PQ || SR and PQ = SR
In quadrilateral PQRS, one pair of opposite sides are equal and parallel to each other.
∴ PQRS is a parallelogram.
In △ BCD, Q and R are the mid-points of side BC and CD respectively.
By mid-point theorem,
⇒ QR || BD and QR = ….(3)
In △ BAD, P and S are the mid-points of side AB and AD respectively.
By mid-point theorem,
PS || BD and PS = …….(4)
From equations (1), (2), (3), (4), we get :
PQ = QR = SR = PS
Hence, proved that the quadrilateral PQRS is a rhombus.
Answered By
2 Likes
Related Questions
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR || AC and SR =
(ii) PQ = SR
(iii) PQRS is a parallelogram

ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
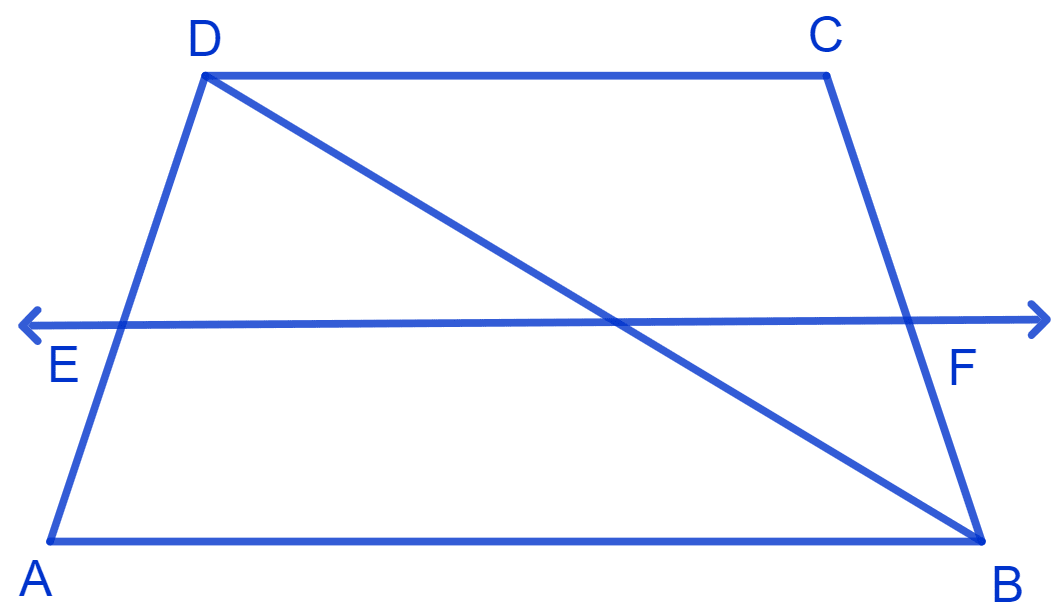
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F see Fig. Show that F is the mid-point of BC.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively see Fig. Show that the line segments AF and EC trisect the diagonal BD.