Mathematics
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR || AC and SR =
(ii) PQ = SR
(iii) PQRS is a parallelogram

Rectilinear Figures
7 Likes
Answer
Given :
ABCD is a quadrilateral, where P, Q, R and S are the mid points of the sides AB, BC, CD and DA.
Mid-point theorem : The line segment joining the mid-points of any two sides of the triangle is parallel to the third side and is half of it.
(i) In △ ADC,
S and R are the mid-points of side AD and CD respectively.
By mid-point theorem,
⇒ SR || AC …….(1)
⇒ SR = ……(2)
Hence, proved that SR || AC and SR = .
(ii) In Δ ABC, P and Q are mid-points of sides AB and BC.
By using the mid-point theorem,
⇒ PQ || AC ………(3)
⇒ PQ = ……(4)
From equations (3) and (4), we get :
⇒ PQ = SR
Hence, proved that PQ = SR.
(iii) From equation (1) and (3), we get :
⇒ PQ || AC || SR
⇒ PQ || SR
Also,
⇒ PQ = SR (Proved above)
We know that,
If one pair of opposite sides are equal and parallel, then the figure is parallelogram.
Hence, proved that PQRS is a parallelogram.
Answered By
3 Likes
Related Questions
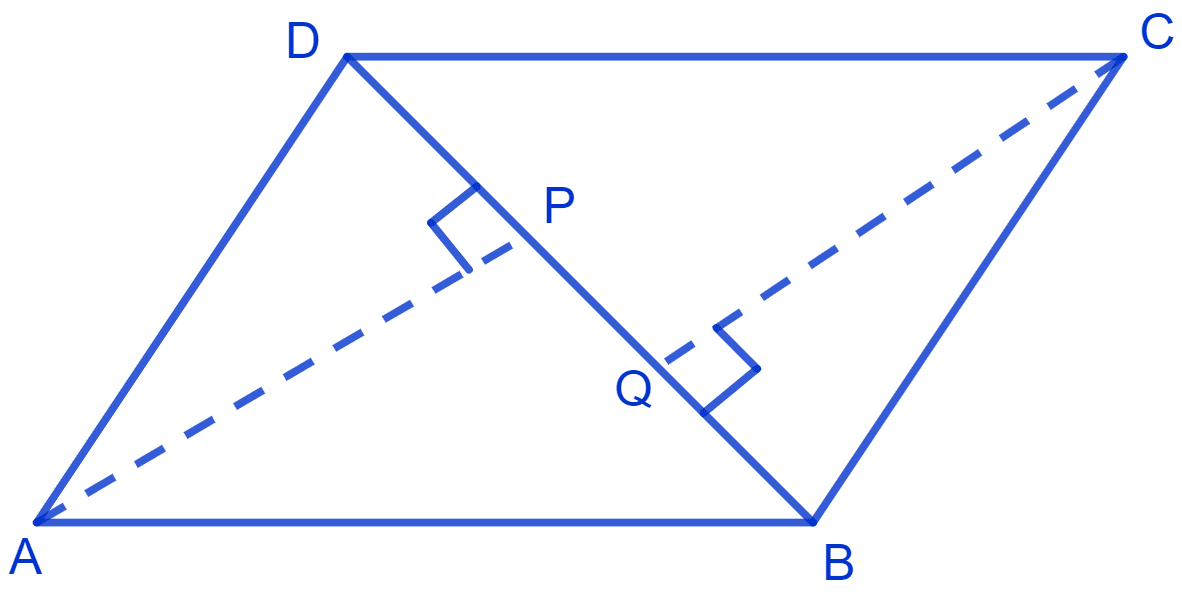
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that
(i) Δ APB ≅ Δ CQD
(ii) AP = CQ
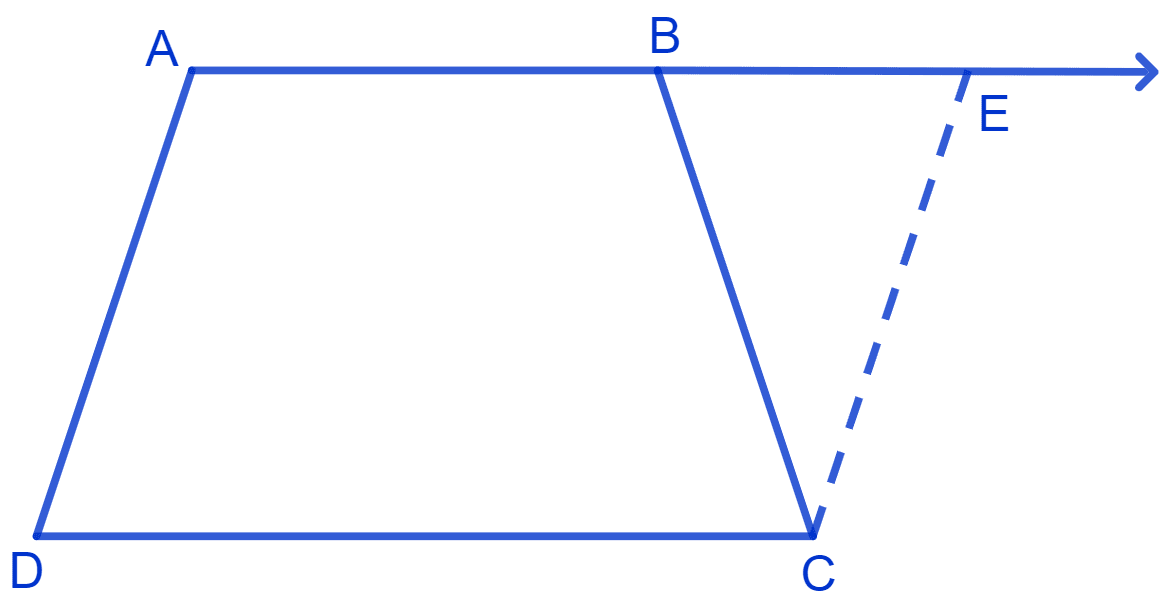
ABCD is a trapezium in which AB || CD and AD = BC. Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) Δ ABC ≅ Δ BAD
(iv) diagonal AC = diagonal BD
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.