Circles

Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.

Answer

Let, there be two circles with center P and X with equal radius.

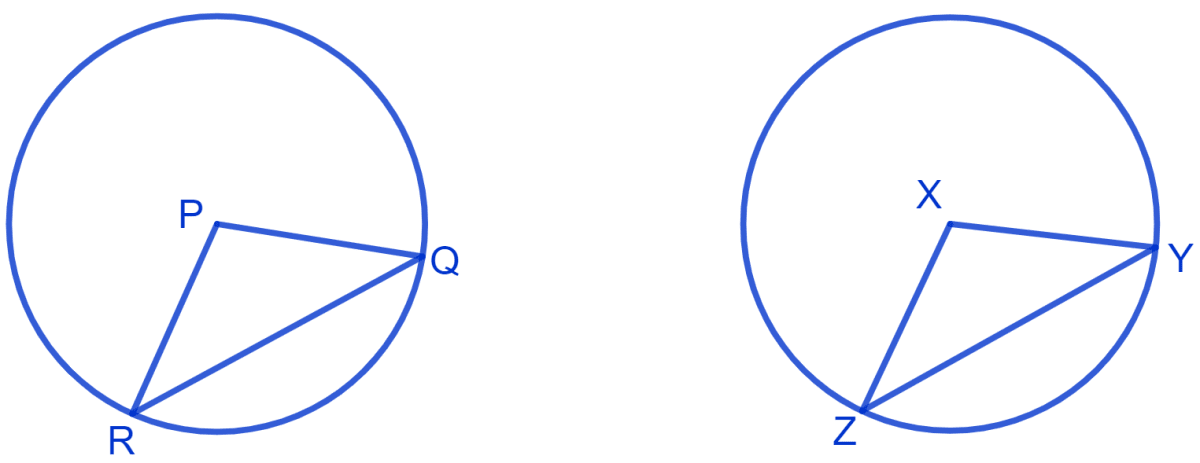
From figure,

QR and YZ are equal chords.

In ∆ PQR and ∆ XYZ,

⇒ PQ = XY (Radius of congruent circles)

⇒ PR = XZ (Radius of congruent circles)

⇒ QR = YZ (Chords are equal)

∴ ∆ PQR ≅ ∆ XYZ (By S.S.S. congruence rule)

We know that,

Corresponding parts of congruent triangles are equal.

⇒ ∠QPR = ∠YXZ (By C.P.C.T.)

Hence, proved that equal chords of congruent circles subtend equal angles at their centers.

Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

Answer

We know that,

The circles are congruent, their radii will be equal.

Let, there be two circles with center P and X with equal radius.

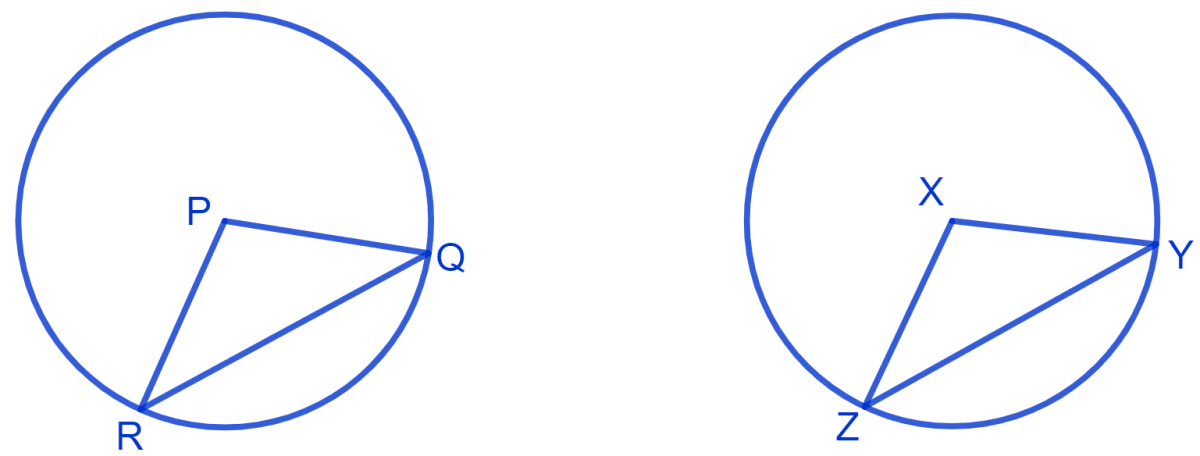
Since,

Chords of congruent circles subtend equal angles at their centres

∴ ∠QPR = ∠YXZ.

⇒ PR = PQ = XZ = XY

In ∆ PQR and ∆ XYZ,

⇒ PQ = XY (Radius of congruent circles are equal)

⇒ ∠QPR = ∠YXZ (Chords subtend equal angles at center)

⇒ PR = XZ (Radius of congruent circles are equal)

∴ ∆ PQR ≅ ∆ XYZ. (By S.A.S. congruence rule)

We know that,

Corresponding parts of congruent triangles are equal.

∴ QR = YZ (By C.P.C.T.)

Hence, proved that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.

Answer

Let the common chord be AB, P and Q be the centers of the two circles.

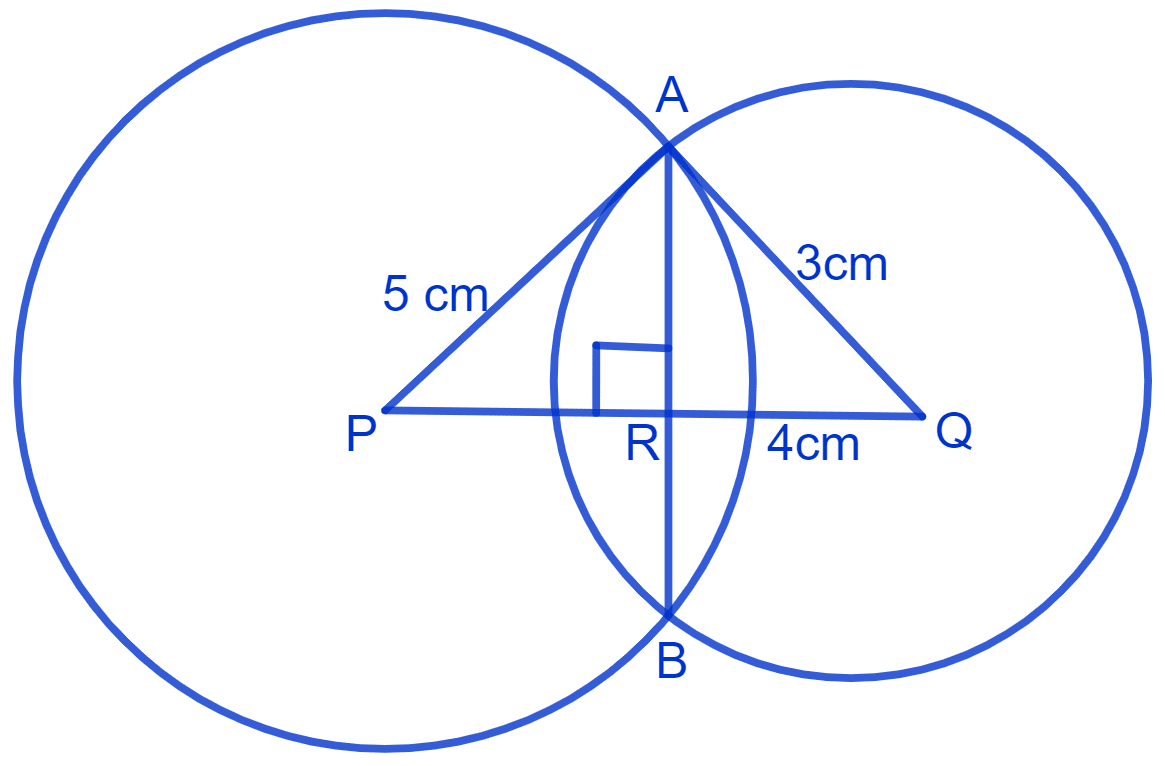
From figure,

⇒ AP = 5 cm and AQ = 3 cm

⇒ PQ = 4 cm (Given)

Join PQ ⊥ AB.

We know that,

Perpendicular from center to the chord, bisects the chord.

⇒ AR = RB = $\dfrac{1}{2}AB$

Let PR = x cm, RQ = (4 - x) cm.

In ∆ ARP,

By pythagoras theorem,

⇒ AP² = AR² + PR²

⇒ AR² = AP² - PR²

⇒ AR² = (5)² - (x)² .......(1)

In ∆ ARQ,

By pythagoras theorem,

⇒ AQ² = AR² + QR²

⇒ AR² = AQ² - QR²

⇒ AR² = 3² - (4 - x)² ........(2)

From equation (1) and (2), we get :

⇒ (5)² - (x)² = (3)² - (4 - x)²

⇒ 25 - x² = 9 - (16 - 8x + x²)

⇒ 25 - x² = 9 - 16 + 8x - x²

⇒ 25 - x² = 8x - x² - 7

⇒ 25 + 7 - x² + x² = 8x

⇒ 32 = 8x

⇒ x = $\dfrac{32}{8}$

⇒ x = 4.

substituting the value of x in equation (1) we get :

⇒ AR² = 5² - 4²

⇒ AR² = 25 - 16

⇒ AR² = 9

⇒ AR = $\sqrt{9}$

⇒ AR = 3 cm.

As,

⇒ AR = $\dfrac{1}{2}AB$

⇒ AB = 2 x AR = 2 x 3 = 6 cm.

Hence, the length of common chord is 6 cm.

If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

Answer

Let AB and CD be the two equal chords (AB = CD = a). Let the chords intersect at point P. Join OP.

Draw OM and ON perpendicular to chords AB and CD respectively.

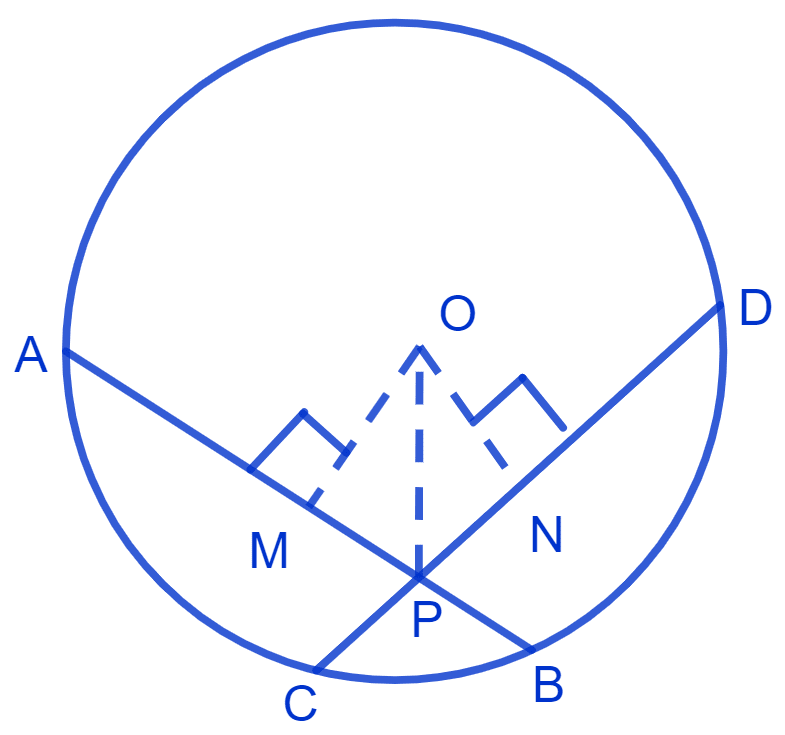
We know that,

Perpendicular from center bisects the chord.

∴ AM = MB = $\dfrac{AB}{2}$ and CN = DN = $\dfrac{CD}{2}$

Since, AB = CD.

∴ AM = MB = CN = DN = x(let) .....(1)

In ∆ OMP and ∆ ONP,

⇒ ∠M = ∠N (Both equal to 90°)

⇒ OP = OP (Common side)

⇒ OM = ON (Equal chords are equidistant from the center.)

∴ ∆ OMP ≅ ∆ ONP (By R.H.S congruence rule)

We know that,

Corresponding parts of congruent triangles are equal.

∴ MP = NP = y(let) (By C.P.C.T.) .....(2)

From figure,

⇒ CP = CN - NP = x - y and PB = MB - MP = x - y

∴ CP = PB.

From figure,

DP = CD - CP = a - (x - y) and AP = AB - BP = a - (x - y)

∴ AP = PD.

Hence, proved that if two equal chords of a circle intersect within the circle, the segments of one chord are equal to corresponding segments of the other chord.

If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.

Answer

Let O be the center of circle, with AB and CD as equal chords.

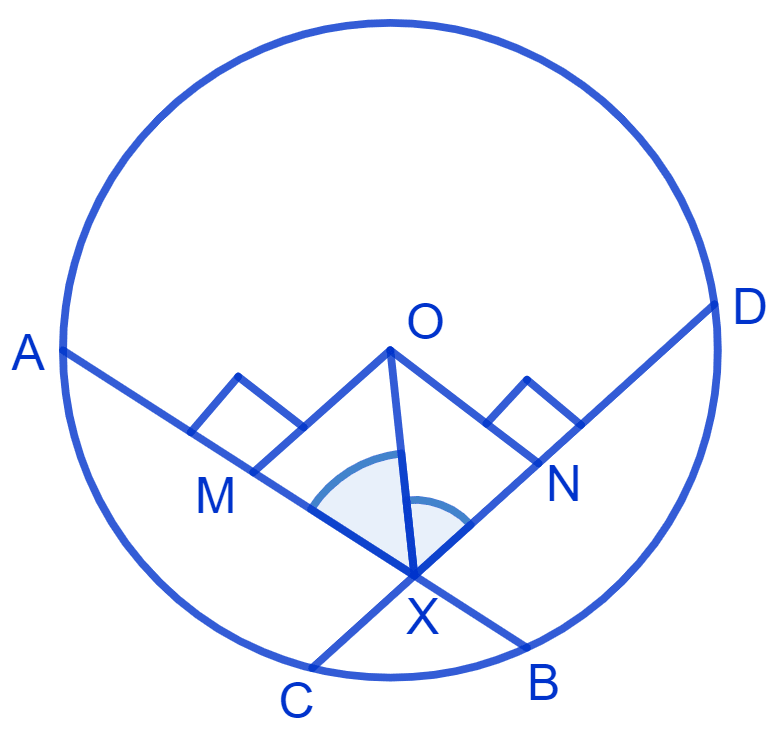
From figure,

X is the point of intersection from the chords.

Draw OM ⊥ AB and ON ⊥ CD.

In ∆ OMX and ∆ ONX,

⇒ ∠OMX = ∠ONX = 90°

⇒ OX = OX (Common)

We know that,

AB and CD are equal chords and equal chords are equidistant from the centre.

⇒ OM = ON

⇒ ∆ OMX ≅ ∆ ONX (By R.H.S. congruence rule)

⇒ ∠OXM = ∠OXN (By C.P.C.T.)

⇒ ∠OXA = ∠OXD

Hence, proved that the line joining the point of intersection to the centre makes equal angles with the chords.

If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD.

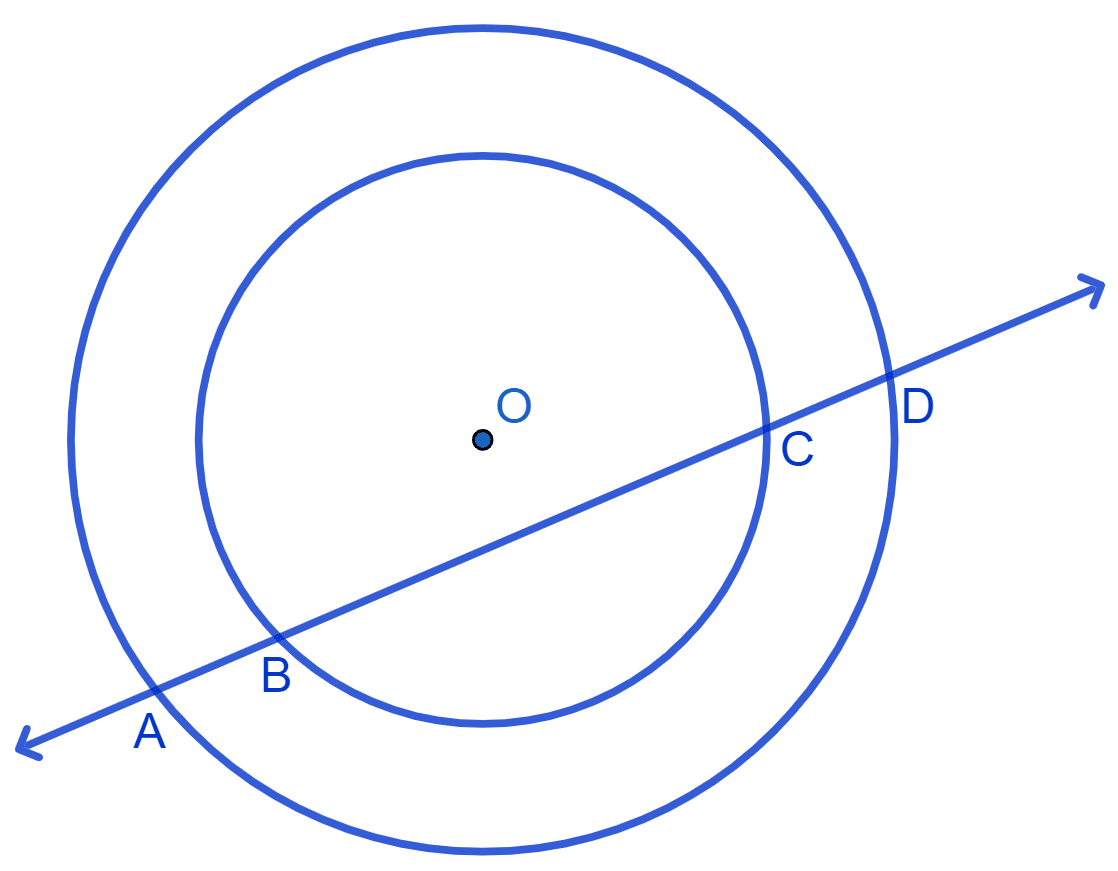
Answer

Draw a perpendicular from the center of the circle to the line AD, such that OM ⊥ AD

BC and AD are the chords of smaller circle and the bigger circle respectively.

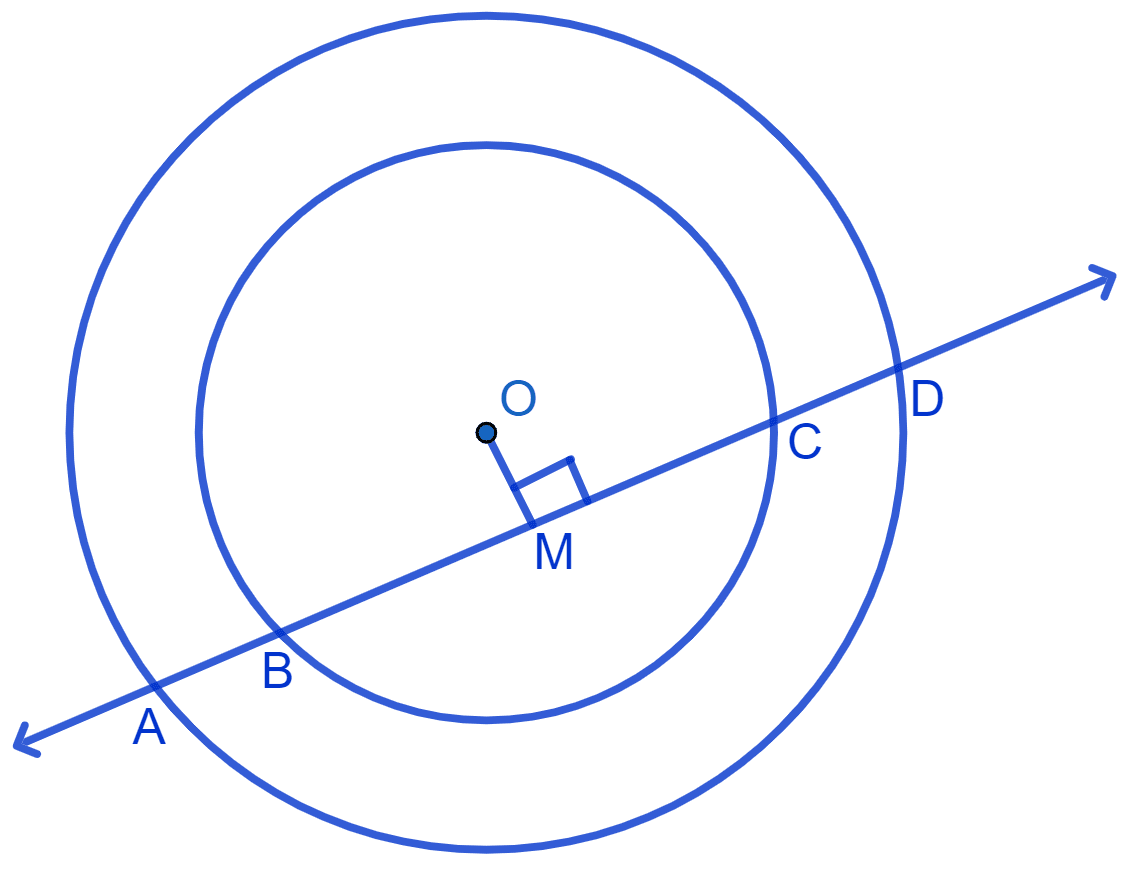
We know that,

Perpendicular from the center bisects the chord.

⇒ BM = MC ......... (1)

⇒ AM = MD ......... (2)

By subtracting equation (1) from (2), we get :

⇒ AM − BM = MD − MC

⇒ AB = CD

Hence, proved that AB = CD.

Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?

Answer

Let R, S and M be the position of Reshma, Salma and Mandip respectively.

From center O,

Draw OA, perpendicular to chord RS and OB, perpendicular to chord SM.

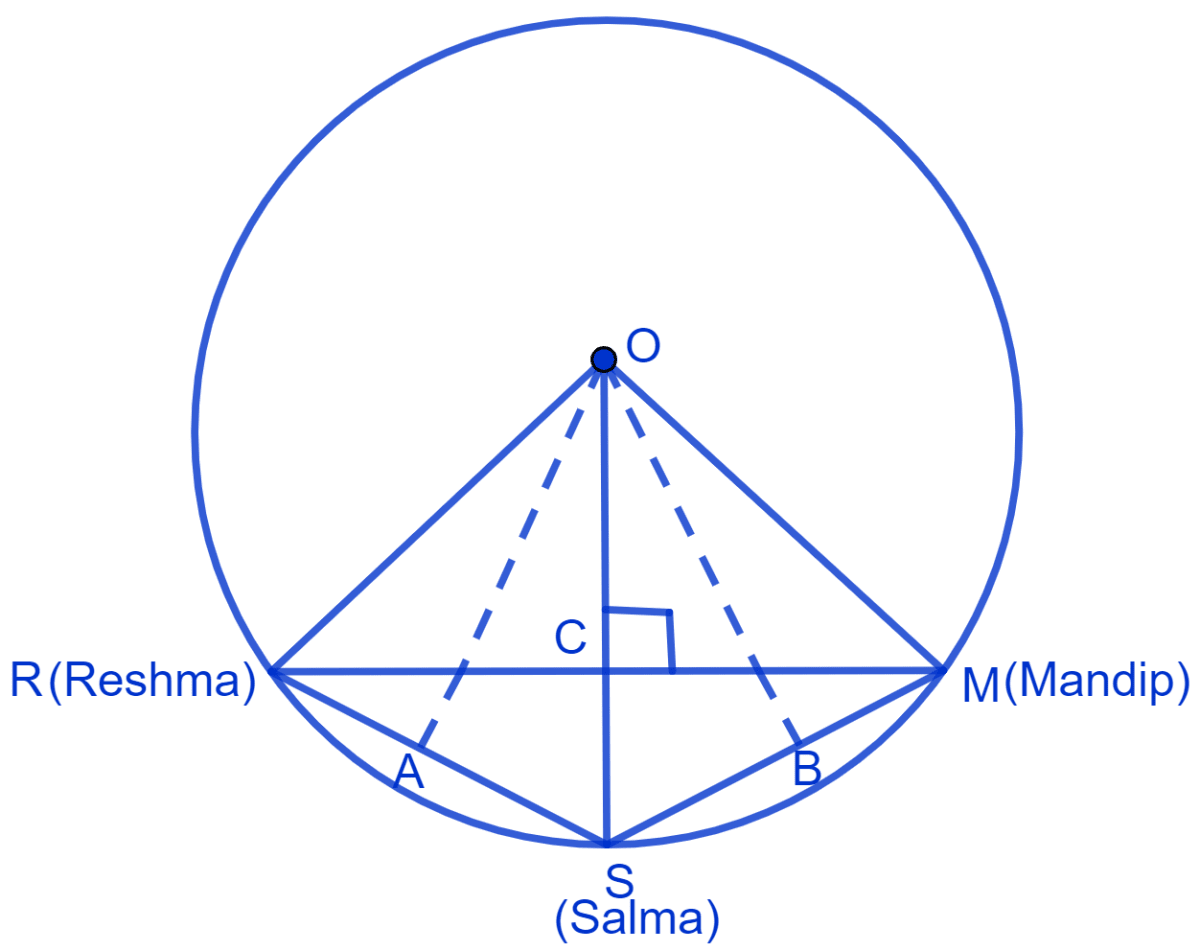
We know that,

Perpendicular from the center to the chord, bisects it.

⇒ AR = AS = $\dfrac{RS}{2} = \dfrac{6}{2}$ = 3 m

From figure,

⇒ OR = OS = OM = 5 m (Radii of circle)

In ∆ OAR,

By pythagoras theorem,

⇒ OR² = OA² + AR²

⇒ (5)² = OA² + (3)²

⇒ 25 = OA² + 9

⇒ OA² = 25 - 9

⇒ OA² = 16

⇒ OA = $\sqrt{16}$

⇒ OA = 4 m

By formula,

Area of triangle = $\dfrac{1}{2} \times$ base x height

Area of ∆ ORS = $\dfrac{1}{2}$ x OA x RS ........(1)

From figure,

In ∆ ORS for base OS, RC is the altitude.

Area of ∆ ORS = $\dfrac{1}{2}$ x OS x RC ........(2)

From equation (1) and (2), we get :

⇒ $\dfrac{1}{2}$ x OS x RC = $\dfrac{1}{2}$ x OA x RS

⇒ $\dfrac{1}{2}$ x RC x 5 = $\dfrac{1}{2}$ x 4 x 6

⇒ RC x 5 = 24

⇒ RC = $\dfrac{24}{5}$

⇒ RC = 4.8 m

As OC is the perpendicular to the chord RM,

∴ OC bisects RM.

⇒ MC = RC

⇒ MC = RC = 4.8 m

⇒ RM = 2 RC = 2 x 4.8 = 9.6 m

Hence, the distance between Reshma and Mandip is 9.6 m.

A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.

Answer

In figure,

A, D and S denote the positions of Ankur, David and Syed, respectively sitting at equal distance.

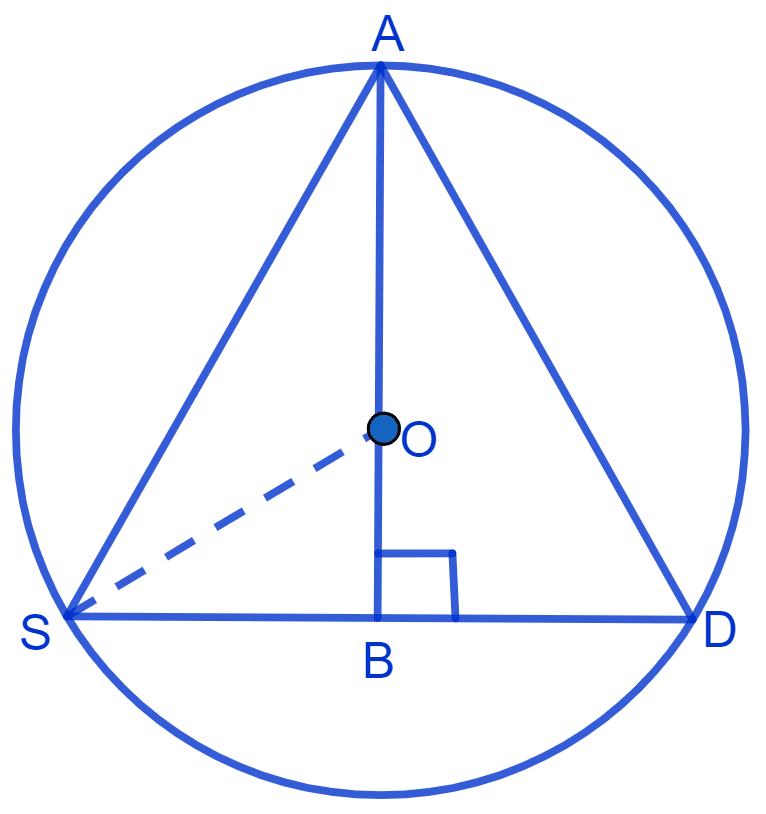
We know that,

If two minor arcs are equal in measure, then their corresponding chords are equal in measure.

∴ AD = DS = SA = 2x (let).

∴ ∆ ADS is an equilateral triangle.

From figure,

Radius = OA = OS = 20 m

Draw AB perpendicular to chord SD.

We know that,

Perpendicular from center bisects the chord.

∴ AB is the median.

∴ BS = BD = $\dfrac{SD}{2} = \dfrac{2x}{2}$ = x.

We know that,

Centre and Centroid are the same for an equilateral triangle, and it divides the median in the ratio 2 : 1.

∴ OA : OB = 2 : 1

$\Rightarrow \dfrac{20}{OB} = \dfrac{2}{1}$

$\Rightarrow OB = \dfrac{20}{2}$ = 10 m.

From figure,

AB = OA + OB = 20 + 10 = 30 m.

In right angle triangle ASB,

By pythagoras theorem,

⇒ AS² = AB² + BS²

⇒ (2x)² = 30² + x²

⇒ 4x² = 900 + x²

⇒ 4x² - x² = 900

⇒ 3x² = 900

⇒ x² = $\dfrac{900}{3}$

⇒ x² = 300

⇒ x = $\sqrt{300} = 10\sqrt{3}$

⇒ 2x = $2 \times 10\sqrt{3} = 20\sqrt{3}$.

Hence, the length of the string of each phone = $20\sqrt{3}$ m.

In Fig. A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.

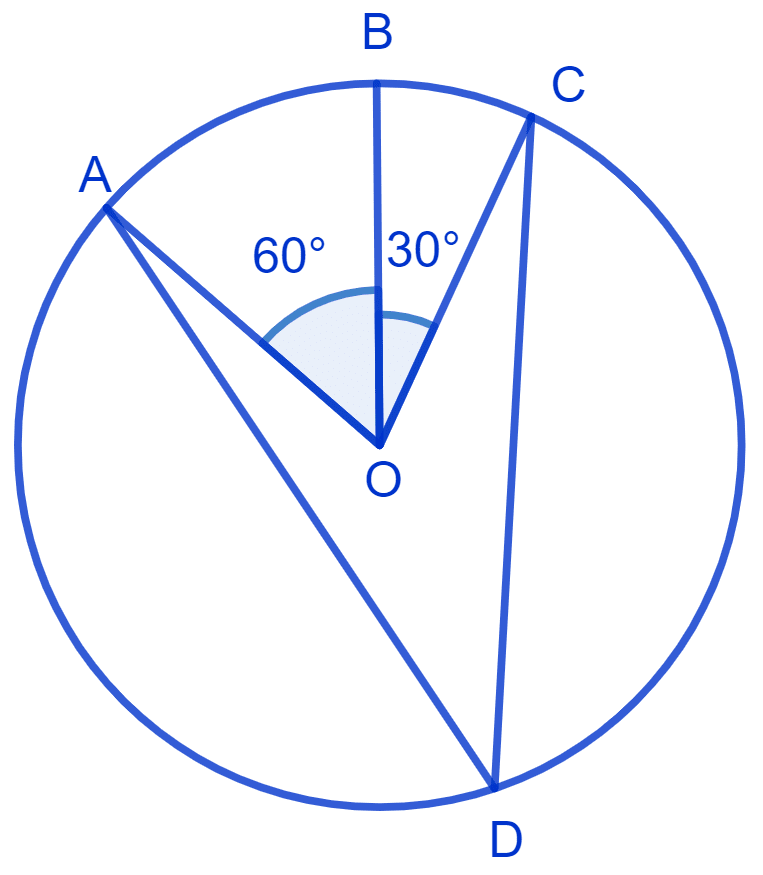
Answer

Given :

⇒ ∠BOC = 30° and ∠AOB = 60°

From figure,

⇒ ∠AOC = ∠AOB + ∠BOC

⇒ ∠AOC = 60° + 30° = 90°.

Arc AC subtends ∠AOC at center of circle and ∠ADC on point D.

We know that,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

⇒ ∠AOC = 2∠ADC

⇒ 2∠ADC = 90°

⇒ ∠ADC = $\dfrac{90°}{2}$ = 45°.

Hence, ∠ADC = 45°.

A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

Answer

From figure,

There is a circle with center O and chord AB which is equal to radius of the circle.

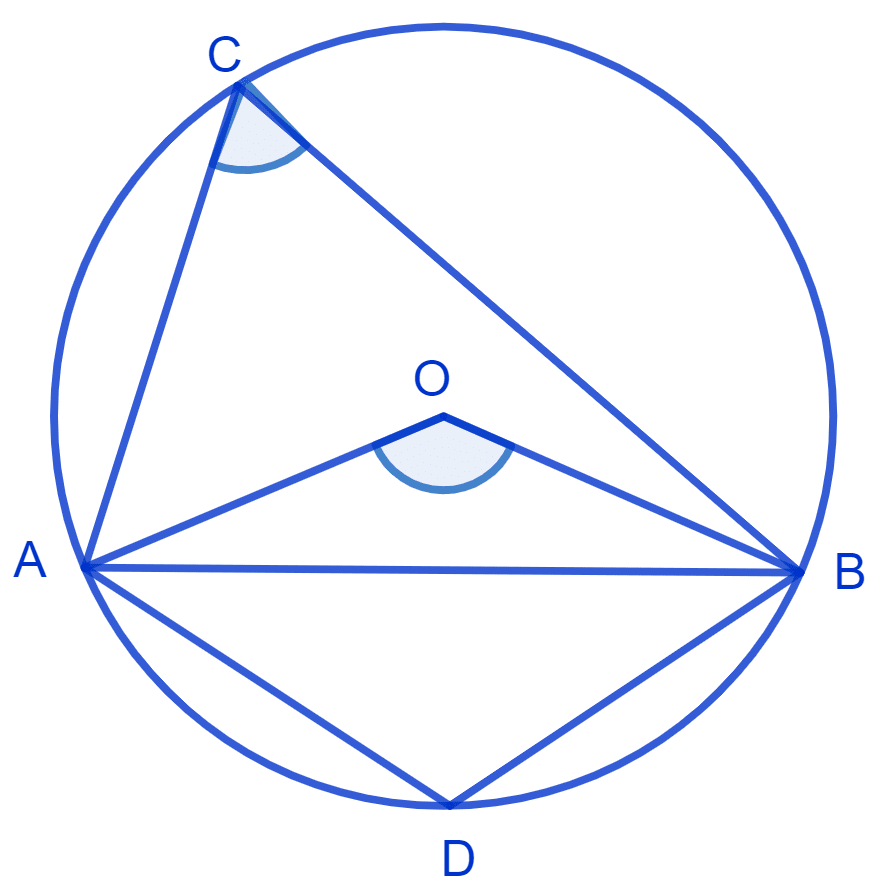
In ∆ AOB,

⇒ OA = OB = AB

∴ ∆ OAB is an equilateral triangle.

⇒ ∠AOB = 60° (Each angle of an equilateral triangle equals to 90°)

We know that,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

⇒ ∠AOB = 2∠ACB

⇒ ∠ACB = $\dfrac{1}{2}$ ∠AOB

⇒ ∠ACB = $\dfrac{1}{2}$ x 60° = 30°

⇒ ∠ACB = 30°.

Since, ACBD is a cyclic quadrilateral

⇒ ∠C + ∠D = 180° (Opposite angles of cyclic quadrilateral are supplementary)

⇒ 30° + ∠D = 180°

⇒ ∠D = 180° - 30°

⇒ ∠D = 150°.

Hence, angle subtended on minor arc equals to 150° and angle subtended on major arc equals 30°.

In Fig. ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

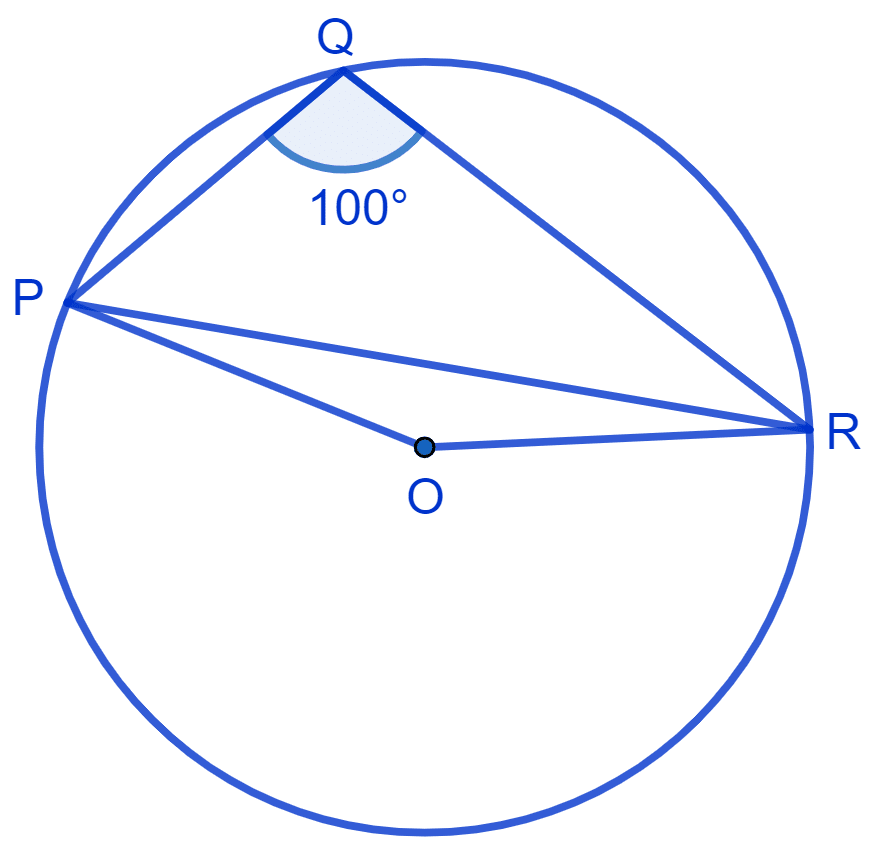
Answer

From figure,

Consider PR as a chord of the circle.

Steps of construction :

1. Mark any point S on the major arc of the circle. (on the side opposite to point Q)

2. Join PS and SR.

PQRS is a cyclic quadrilateral.

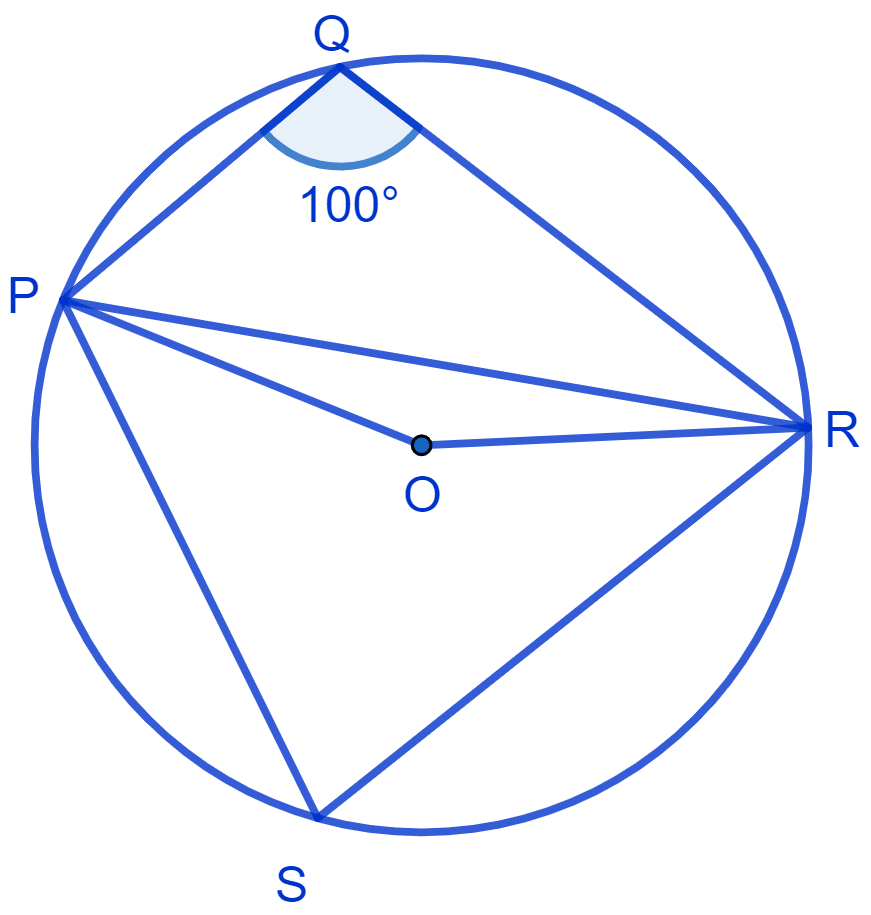
⇒ ∠PQR + ∠PSR = 180° (Sum of opposite angles in a cyclic quadrilateral = 180°)

⇒ 100° + ∠PSR = 180°

⇒ ∠PSR = 180° - 100° = 80°.

We know that,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠POR = 2∠PSR

⇒ ∠POR = 2 × 80°

⇒ ∠POR = 160°.

In ∆ OPR,

⇒ OP = OR (Radius of the circle)

We know that,

Angles opposite to equal sides are equal.

∴ ∠OPR = ∠ORP = a (let).

We know that,

Sum of all angles in a triangle is 180°.

⇒ ∠OPR + ∠POR + ∠ORP = 180°

⇒ a + 160° + a = 180° [∵ ∠OPR = ∠ORP]

⇒ 2a = 180° - 160°

⇒ 2a = 20°

⇒ a = $\dfrac{20°}{2}$ = 10°

⇒ ∠OPR = 10°.

Hence, ∠OPR = 10°.

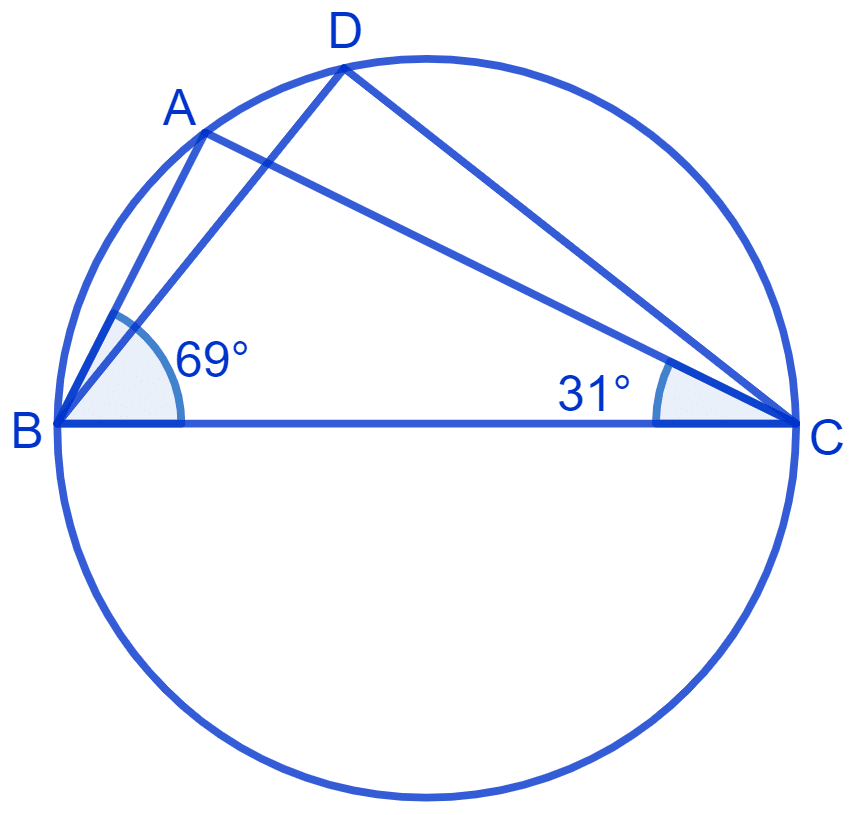
In Fig. ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

Answer

In ∆ ABC,

⇒ ∠ABC + ∠BAC + ∠ACB = 180° (Angle sum property of a triangle)

⇒ 69° + ∠BAC + 31° = 180°

⇒ ∠BAC + 100° = 180°

⇒ ∠BAC = 180° - 100°

⇒ ∠BAC = 80°

We know that,

Angles in the same segment of a circle are equal.

So, ∠BDC = ∠BAC = 80°.

Hence, ∠BDC = 80°.

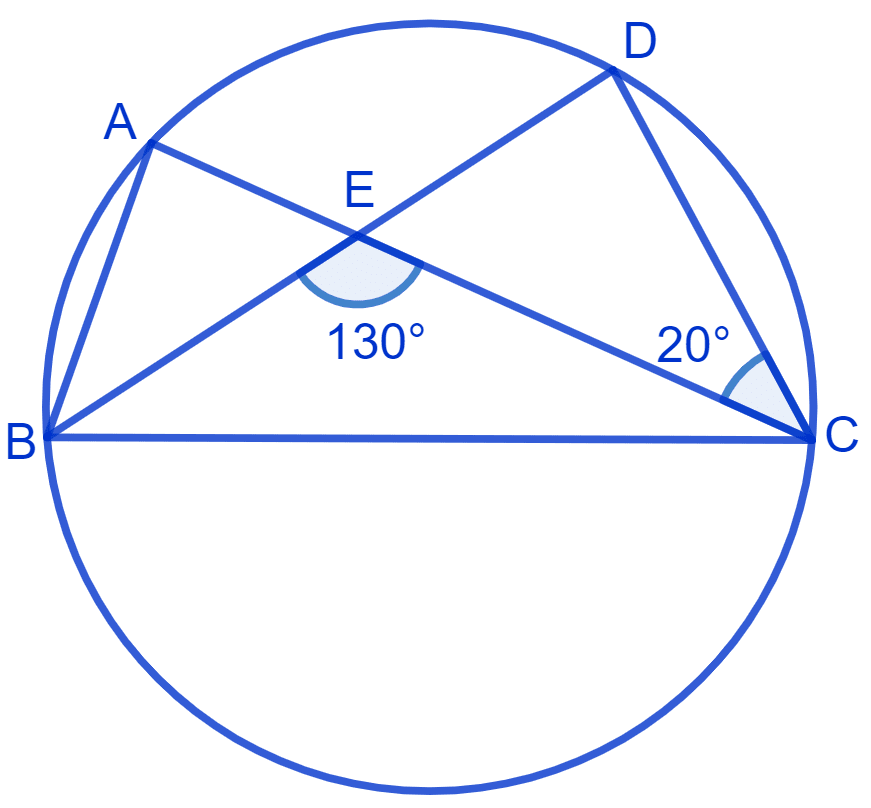
In Fig. A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.

Answer

From figure,

BD is a straight line

⇒ ∠BEC + ∠DEC = 180° (Linear pairs)

⇒ 130° + ∠DEC = 180°

⇒ ∠DEC = 180° - 130°

⇒ ∠DEC = 50°.

In ∆ DEC,

⇒ ∠DEC + ∠EDC + ∠ECD = 180° (Angle sum property of a triangle)

⇒ 50° + ∠EDC + 20° = 180°

⇒ ∠EDC + 70° = 180°

⇒ ∠EDC = 180° - 70°

⇒ ∠EDC = 110°.

From figure,

⇒ ∠BDC = ∠EDC = 110°

We know that,

Angles in the same segment of a circle are equal.

⇒ ∠BAC = ∠BDC = 110°.

Hence, ∠BAC = 110°.

ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.

Answer

Cyclic quadrilateral ABCD is shown in the figure below:

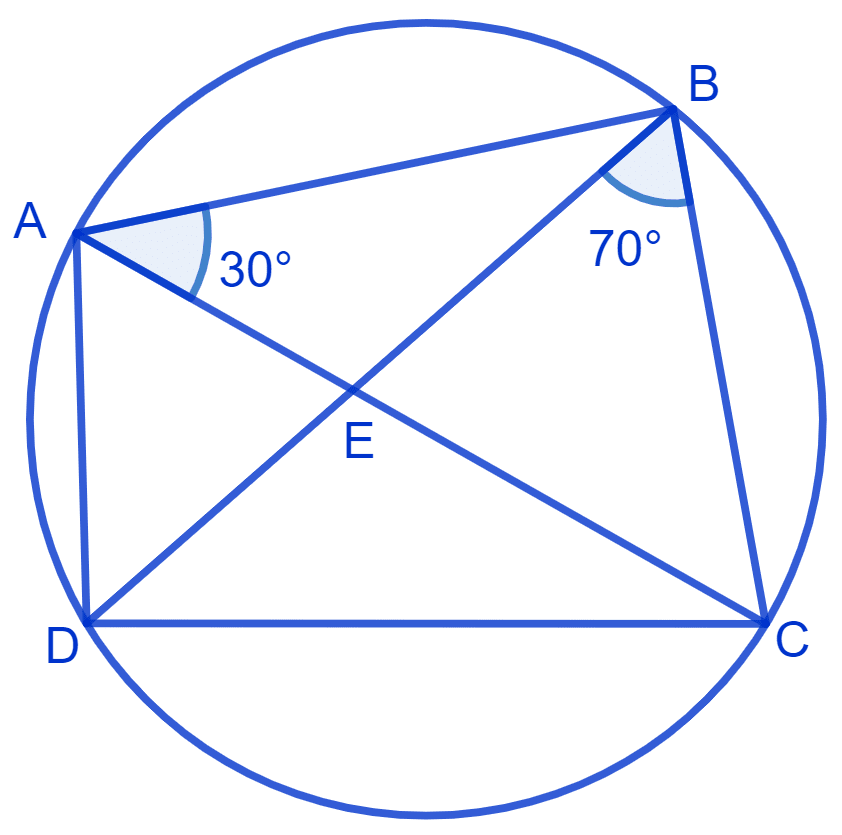
∠CAD = ∠CBD = 70° (Angles in the same segment are equal)

From figure,

⇒ ∠BAD = ∠CAB + ∠DAC

⇒ ∠BAD = 30° + 70°

⇒ ∠BAD = 100°.

Since ABCD is a cyclic quadrilateral, the sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠BAD + ∠BCD = 180°

⇒ ∠BCD = 180° - ∠BAD

⇒ ∠BCD = 180° - 100° = 80°

Given, AB = BC

In △ ABC,

⇒ ∠BCA = ∠BAC = 30° (Angles opposite to equal sides are equal)

From figure,

⇒ ∠ECD = ∠BCD - ∠BCA

⇒ ∠ECD = 80° - 30° = 50°.

Hence, ∠BCD = 80° and ∠ECD = 50°.

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Answer

Let ABCD be a cyclic quadrilateral where diagonal AC and BD are diameters.

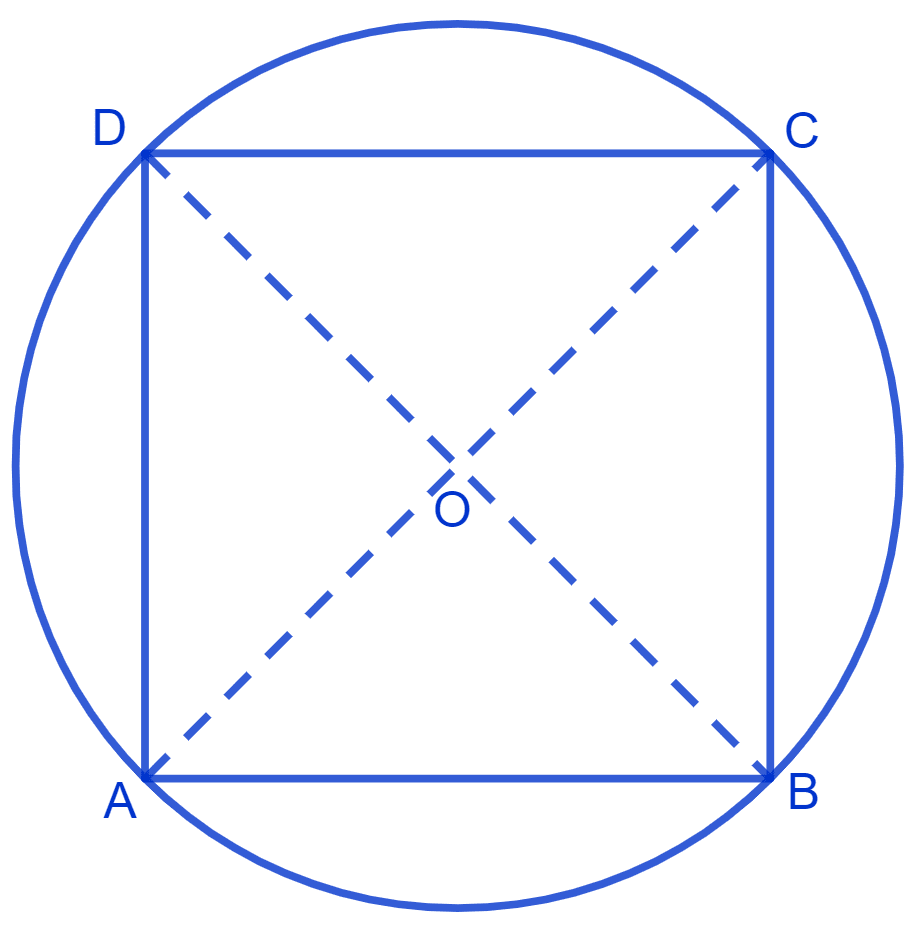
Since BD is a diameter.

Arc BAD is a semicircle, So ∠BAD = 90° (Angle in a semi circle is a right angle)

Since AC ia a diameter.

Arc ABC is a semicircle, So ∠ABC = 90° (Angle in a semi circle is a right angle)

Also,

ABCD is a cyclic quadrilateral

From figure,

⇒ ∠BCD + ∠BAD = 180° (Sum of opposite angles of cyclic quadrilateral is 180°)

⇒ ∠BCD + 90° = 180°

⇒ ∠BCD = 180° - 90°

⇒ ∠BCD = 90°.

⇒ ∠ABC + ∠ADC =180° (Sum of opposite angles of cyclic quadrilateral is 180°)

⇒ ∠ADC + 90° = 180°

⇒ ∠ADC = 180° - 90°

⇒ ∠ADC = 90°.

So, in quadrilateral ABCD

∠A = ∠B = ∠C = ∠D = 90°

Since, all angles equal to 90°.

Hence, proved that ABCD is a rectangle.

If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

Answer

ABCD is a trapezium where AB || DC and AD = BC.

Draw DM and CN perpendicular to AB.

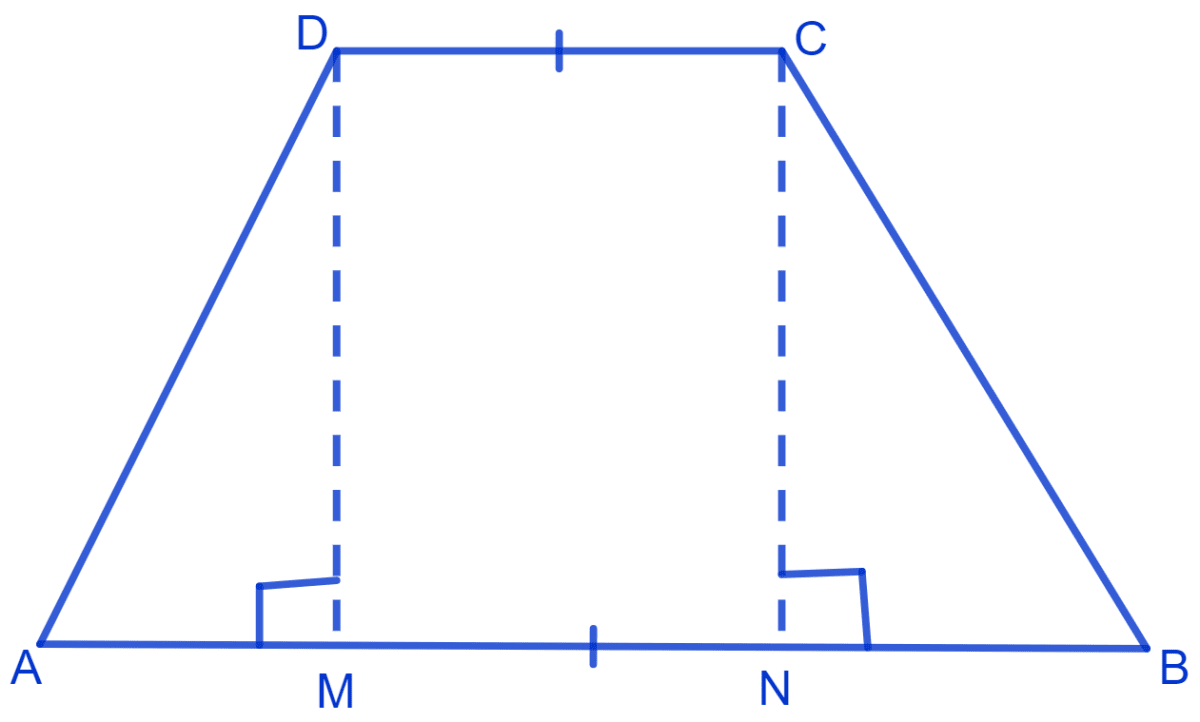
In Δ DAM and Δ CBN,

⇒ AD = BC (Given)

⇒ ∠AMD = ∠BNC (Right angles)

⇒ DM = CN (Perpendicular distance between parallel lines are equal)

∴ ∆ DAM ≅ ∆ CBN, (By R.H.S. congruence rule)

We know that,

Corresponding part of congruent triangle are equal.

⇒ ∠A = ∠B (By C.P.C.T.) .....(1)

From figure,

⇒ ∠B + ∠C = 180° (Sum of the co-interior angles = 180°)

Substituting value of ∠B from equation (1) in above equation, we get :

⇒ ∠A + ∠C = 180°

We know that,

Sum of angles in a quadrilateral = 360°.

∴ ∠A + ∠B + ∠C + ∠D = 360°

⇒ (∠A + ∠C) + (∠B + ∠D) = 360°

⇒ 180° + (∠B + ∠D) = 360°

⇒ (∠B + ∠D) = 360° - 180°

⇒ (∠B + ∠D) = 180°.

ABCD is a cyclic quadrilateral as the sum of the pair of opposite angle is 180°.

Hence, if the non-parallel sides of a trapezium are equal, it is cyclic.

Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.

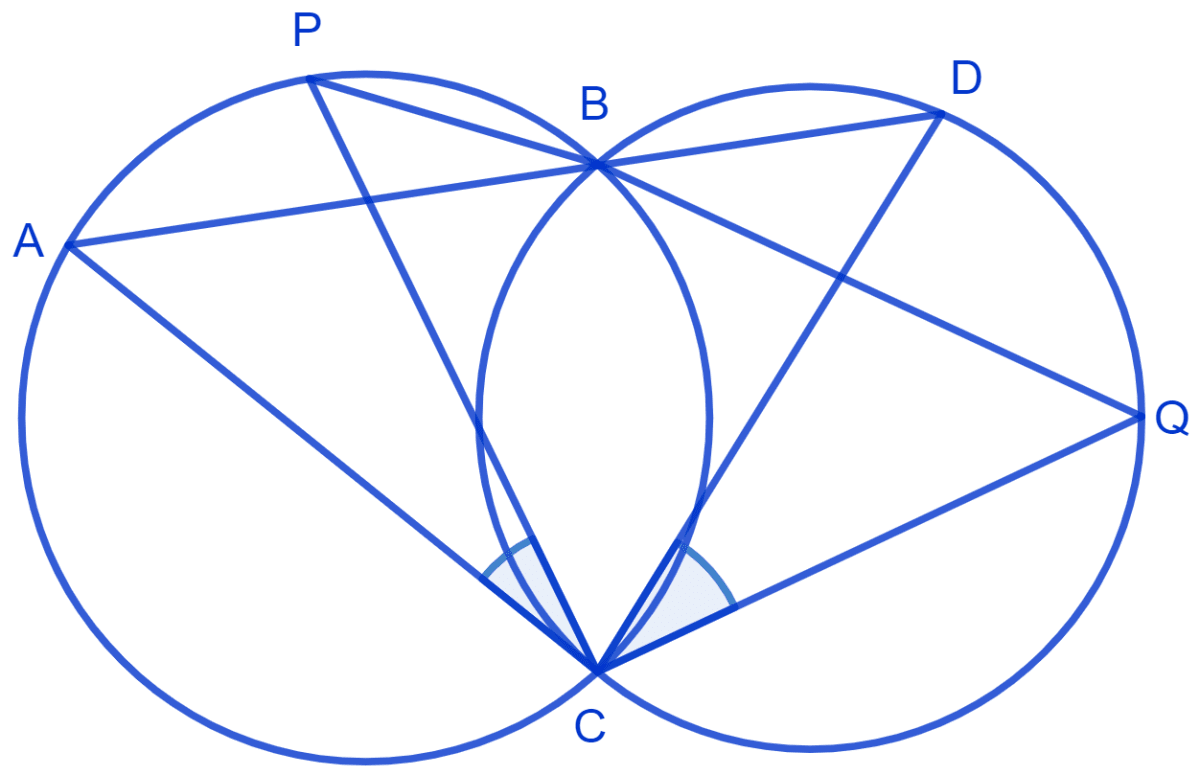
Answer

Join chord AP and DQ.

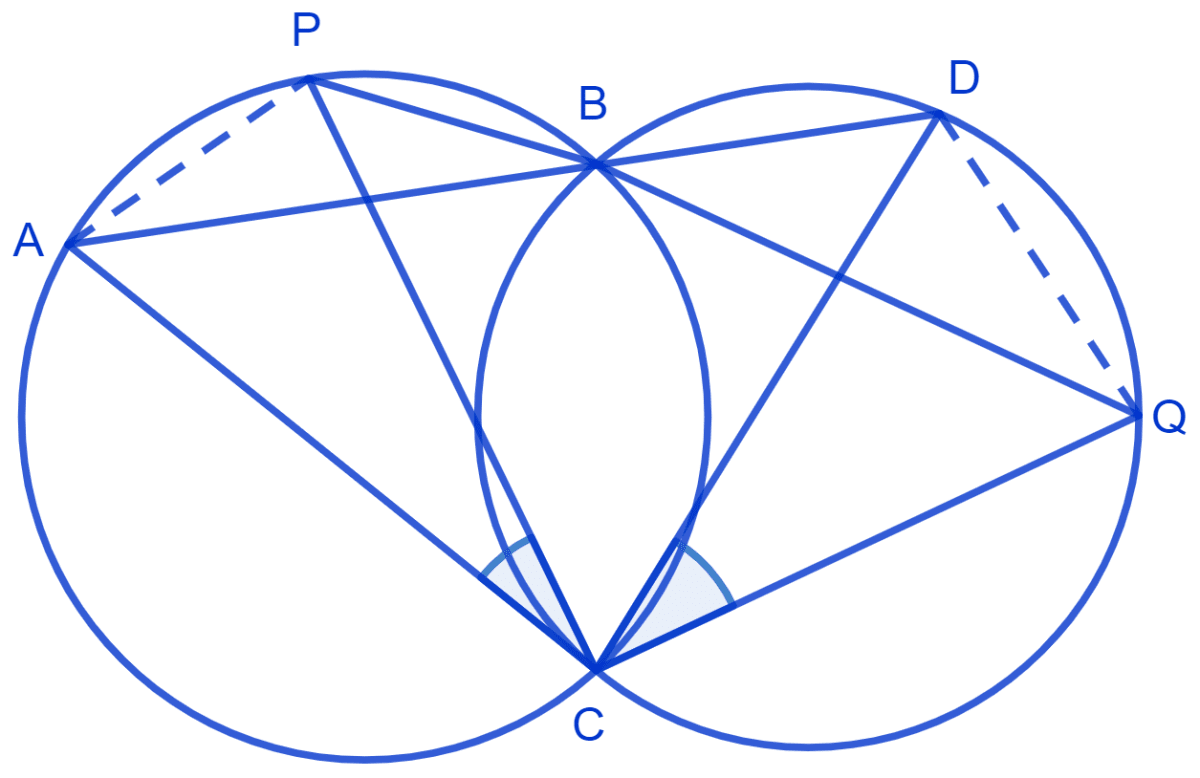
For chord AP,

⇒ ∠PBA = ∠ACP (Angles in the same segment are equal) .....(1)

For chord DQ,

⇒ ∠DBQ = ∠QCD (Angles in the same segment are equal) .....(2)

ABD and PBQ are line segments intersecting at B.

⇒ ∠PBA = ∠DBQ (Vertically opposite angles are equal) ....(3)

From equation (1) and (3) we get :

⇒ ∠DBQ = ∠ACP ...........(4)

From equation (2) and (4) we get :

⇒ ∠QCD = ∠ACP.

Hence, proved that ∠ACP = ∠QCD.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Answer

Two circles are drawn taking sides AB and AC as diameter.

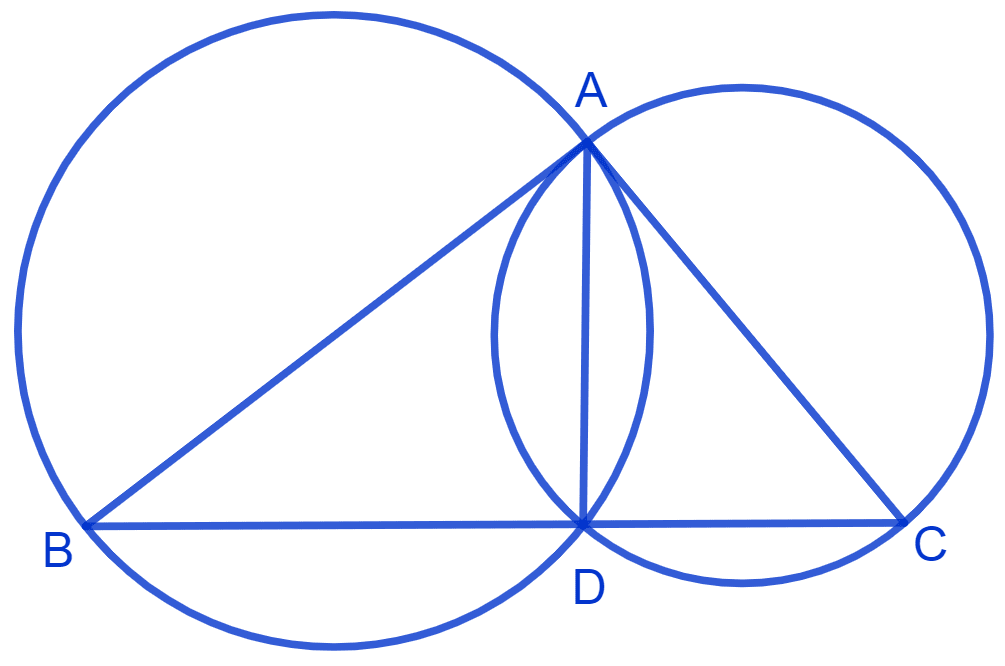
⇒ ∠ADB = ∠ADC = 90° (Angles in the semi circle is a right angle.)

⇒ ∠ADB + ∠ADC = 90° + 90°

⇒ ∠ADB + ∠ADC = 180°

∴ BDC is straight line.

Thus, D lies on BC.

Hence, proved that the point of intersection of circles lie on the third side.

ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.

Answer

Δ ABC and Δ ADC are shown in the figure below:

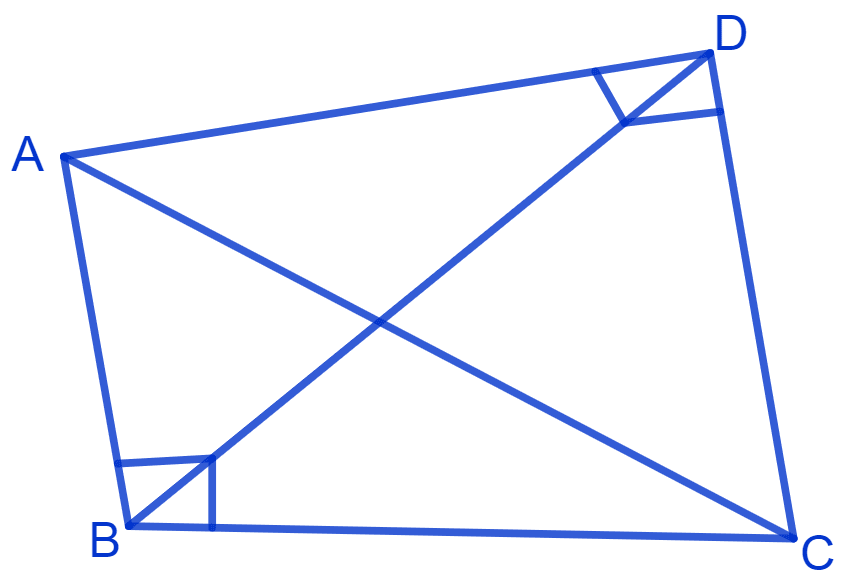
From figure,

In ∆ ABC and ∆ ADC,

⇒ ∠B = 90° and ∠D = 90° [∵ ∆ ABC and ∆ ADC are right angled triangles]

We know that,

The sum of angles in a triangle is 180°.

If the sum of pair of opposite angles in a quadrilateral is 180°, then it is a cyclic quadrilateral.

In Δ ABC,

⇒ ∠ABC + ∠BCA + ∠CAB = 180° (Angle sum property of triangle)

⇒ 90° + ∠BCA + ∠CAB = 180°

⇒ ∠BCA + ∠CAB = 180° - 90°

⇒ ∠BCA + ∠CAB = 90° .....(1)

In Δ ADC,

⇒ ∠CDA + ∠ACD + ∠DAC = 180° (Angle sum property of triangle)

⇒ 90° + ∠ACD + ∠DAC = 180°

⇒ ∠ACD + ∠DAC = 180° - 90°

⇒ ∠ACD + ∠DAC = 90° .....(2)

Adding equation (1) and (2), we get :

⇒ ∠BCA + ∠CAB + ∠ACD + ∠DAC = 180°

⇒ (∠BCA + ∠ACD) + (∠CAB + ∠DAC) = 180°

⇒ ∠BCD + ∠DAB = 180° .....(3)

⇒ ∠B + ∠D = 90° + 90° = 180° .....(4)

Since, sum of opposite angles of quadrilateral ABCD is 180°. Therefore, it is a cyclic quadrilateral.

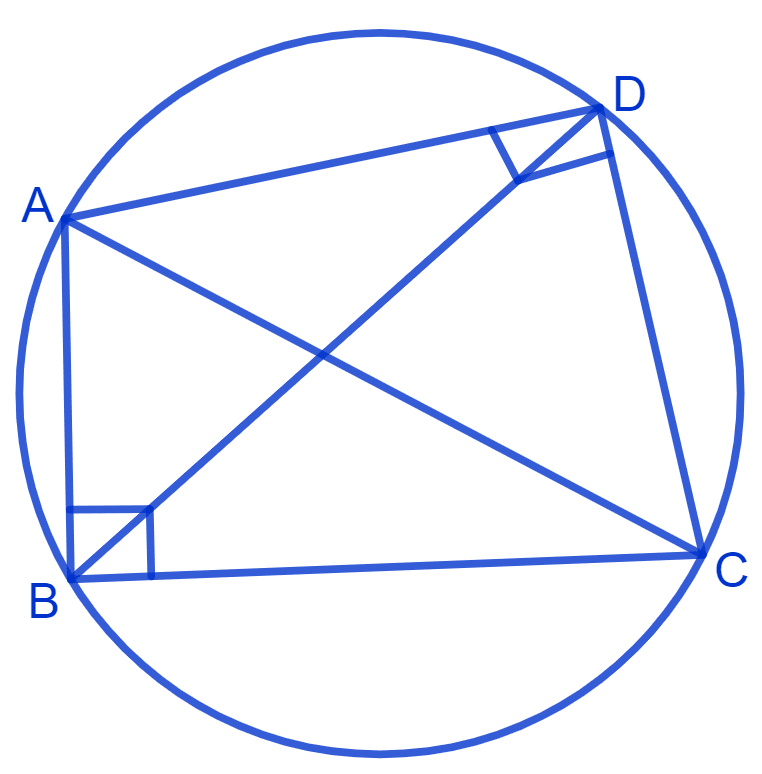
We know that,

Angles in the same segment are equal.

⇒ ∠CAD = ∠CBD.

Hence, proved that ∠CAD = ∠CBD.

Prove that a cyclic parallelogram is a rectangle.

Answer

Let ABCD be the cyclic parallelogram.

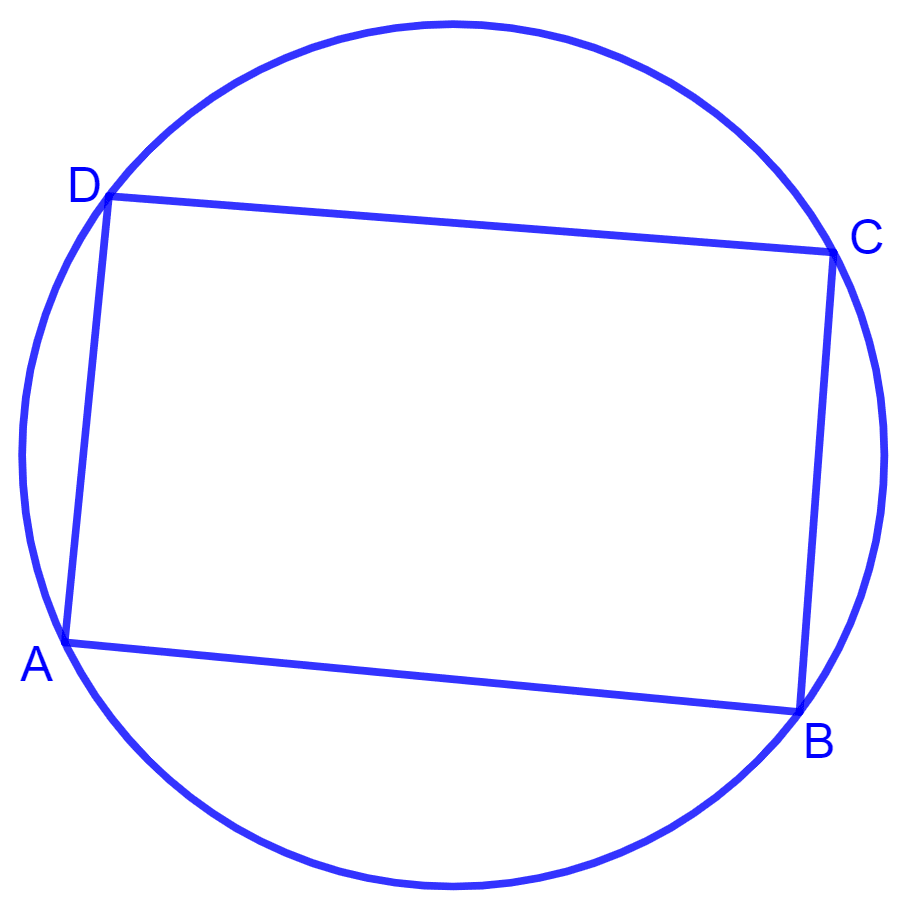
We know that opposite angles of a parallelogram are equal.

⇒ ∠A = ∠C .......(1)

⇒ ∠B = ∠D .......(2)

We know that the sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠A + ∠C = 180°

⇒ ∠A + ∠A = 180° (From equation (1))

⇒ 2∠A = 180°

⇒ ∠A = $\dfrac{180°}{2}$

⇒ ∠A = 90°.

We know that,

If one angle of a parallelogram is 90°, then it is a rectangle.

Thus, quadrilateral ABCD is a rectangle.

Hence, proved that a cyclic parallelogram is a rectangle.