Lines and Angles

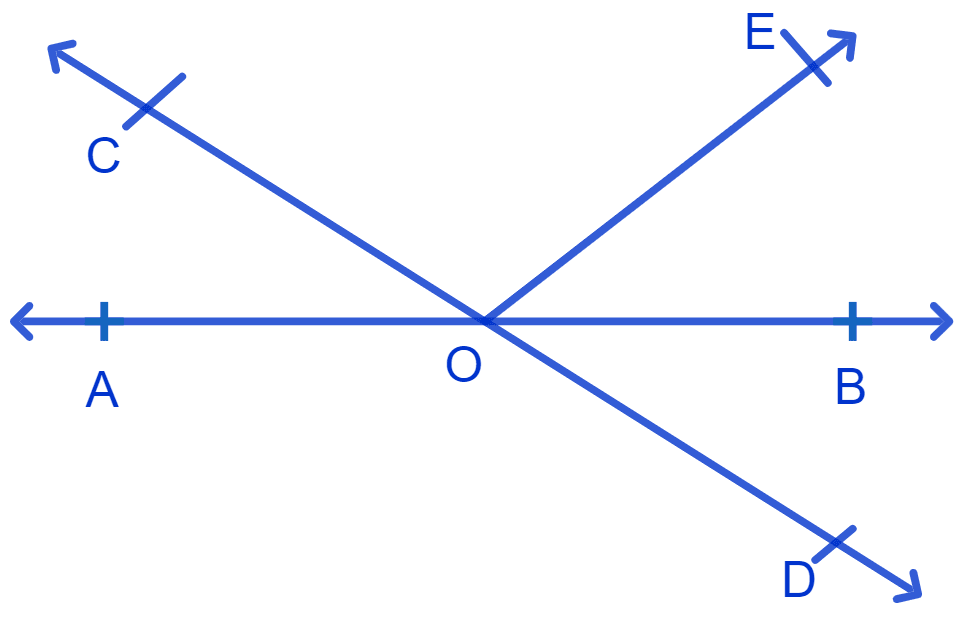
In Fig. lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Answer

Given :

∠BOD = 40°

From figure,

⇒ ∠AOC = ∠BOD (Vertically opposite angles are equal)

⇒ ∠AOC = 40°

Given,

⇒ ∠AOC + ∠BOE = 70°

⇒ ∠BOE = 70° - ∠AOC = 70° - 40° = 30°.

Since, AB is a straight line.

From figure :

⇒ ∠AOC + ∠COE + ∠BOE = 180° [Linear pairs]

⇒ ∠COE + (∠AOC + ∠BOE) = 180°

⇒ ∠COE + (40° + 30°) = 180°

⇒ ∠COE + 70° = 180°

⇒ ∠COE = 180° - 70° = 110°.

⇒ Reflex ∠COE = 360° - ∠COE = 360° - 110° = 250°.

Hence, ∠BOE = 30° and Reflex ∠COE = 250°.

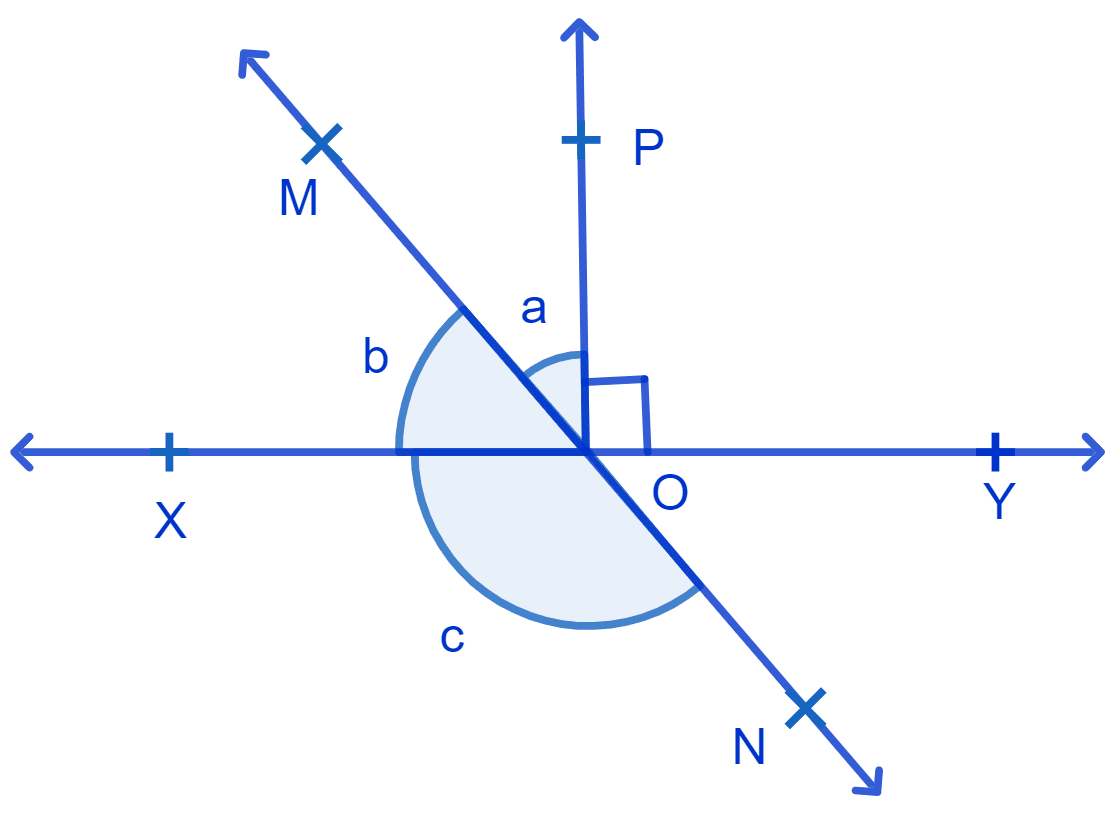
In Fig. lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

Answer

Since,

∠POY = 90°

Line OP is perpendicular to line XY. Hence ∠POY = ∠POX = 90°

Given, a : b = 2 : 3

Let a = 2x and b = 3x, where x is some number.

From figure,

⇒ ∠POX + ∠POY = 180° (Linear pairs)

⇒ ∠POM + ∠MOX + ∠POY = 180°

⇒ a + b + 90° = 180°

⇒ 2x + 3x = 180° - 90°

⇒ 5x = 90°

⇒ x = $\dfrac{90°}{5}$

⇒ x = 18°.

⇒ a = 2x = 2(18°) = 36°

⇒ b = 3x = 3(18°) = 54°

Since MN is a straight line,

⇒ ∠MOX + ∠XON = 180° (Linear pairs)

⇒ b + c = 180°

⇒ 54° + c = 180°

⇒ c = 180° - 54°

⇒ c = 126°.

Hence, c = 126°.

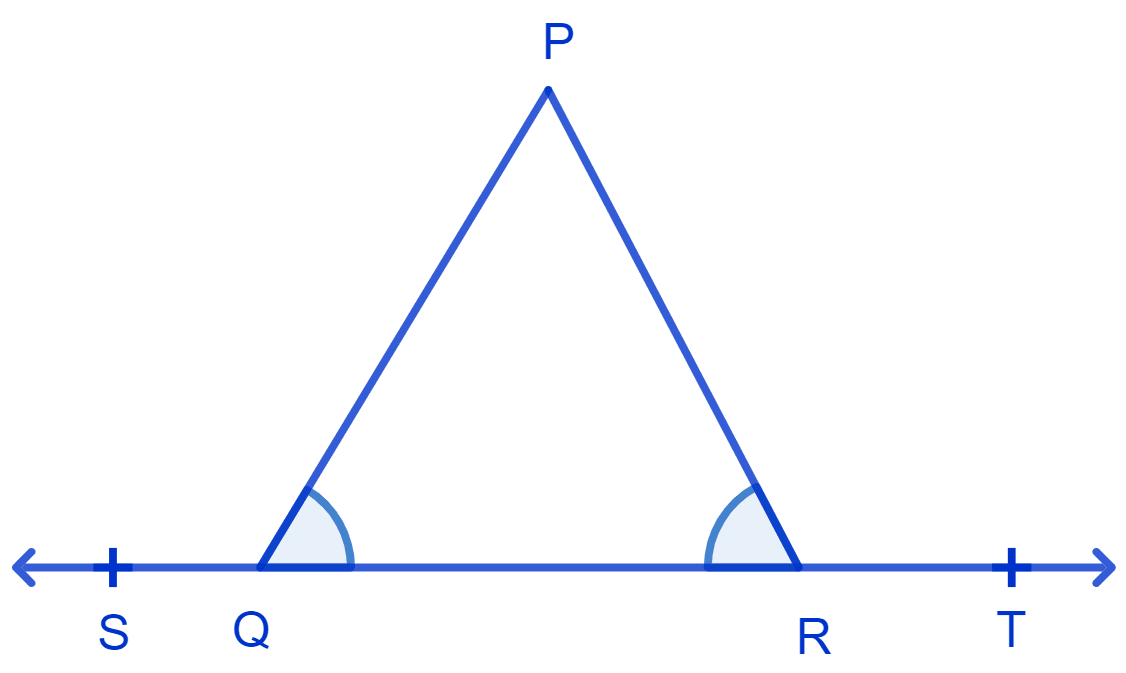
In Fig. ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Answer

Given,

⇒ ∠PQR = ∠PRQ = x (let)

From figure,

⇒ ∠PQS + ∠PQR = 180° (Linear pair)

⇒ ∠PQS = 180° - ∠PQR

⇒ ∠PQS = 180° - x .......(1)

From figure,

⇒ ∠PRT + ∠PRQ = 180°

⇒ ∠PRT = 180° - ∠PRQ

⇒ ∠PRT = 180° - x .........(2)

From equations, (1) and (2) we get :

⇒ ∠PQS = ∠PRT

Hence, proved ∠PQS = ∠PRT.

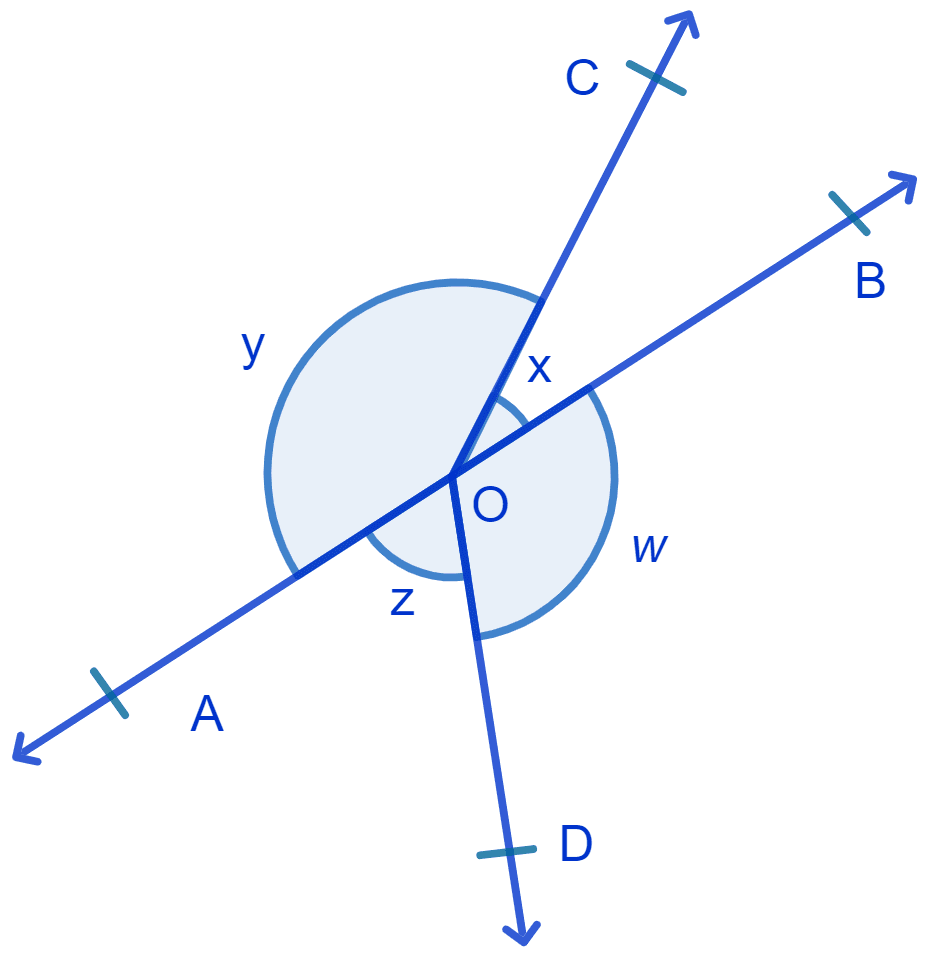
In Fig. if x + y = w + z, then prove that AOB is a line.

Answer

We know that,

Sum of all angles round a point is equal to 360°.

⇒ x + y + w + z = 360°

⇒ (x + y) + (w + z) = 360°

As,

x + y = w + z

⇒ (x + y) + (x + y) = 360°

⇒ 2(x + y) = 360°

⇒ (x + y) = $\dfrac{360°}{2}$ = 180°.

⇒ x + y = 180° and w + z = 180°.

Since the sum of adjacent angles, x and y with OA and OB as the non-common arms is 180° we can say that AOB is a straight line.

Hence, proved that AOB is a straight line.

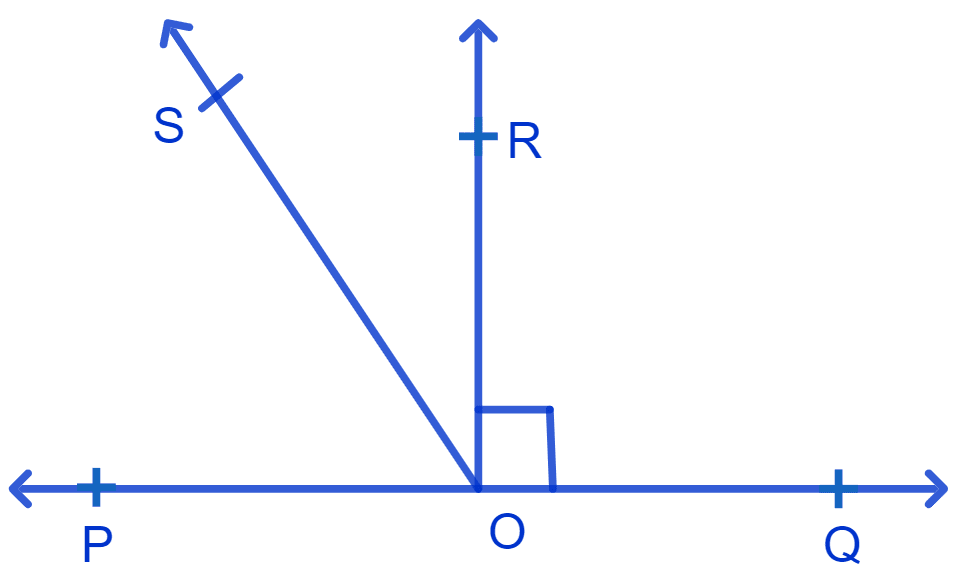
In Fig. POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that

∠ROS = $\dfrac{1}{2}$ (∠QOS – ∠POS).

Answer

Since, OR ⊥ PQ

∴ ∠ROP = 90° and ∠ROQ = 90°

∴ ∠ROS = 90° - ∠POS .......(1)

⇒ ∠QOS = ∠QOR + ∠ROS

⇒ ∠QOS = 90° + ∠ROS

⇒ 90° = ∠QOS - ∠ROS .....(2)

Substituting value of 90° from equation (2) in equation (1), we get :

⇒ ∠ROS = (∠QOS - ∠ROS) - ∠POS

⇒ ∠ROS + ∠ROS = ∠QOS - ∠POS

⇒ 2(∠ROS) = ∠QOS - ∠POS

⇒ ∠ROS = $\dfrac{1}{2}$ (∠QOS - ∠POS)

Hence, proved ∠ROS = $\dfrac{1}{2}$ (∠QOS - ∠POS).

It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.

Answer

The figure is shown below:

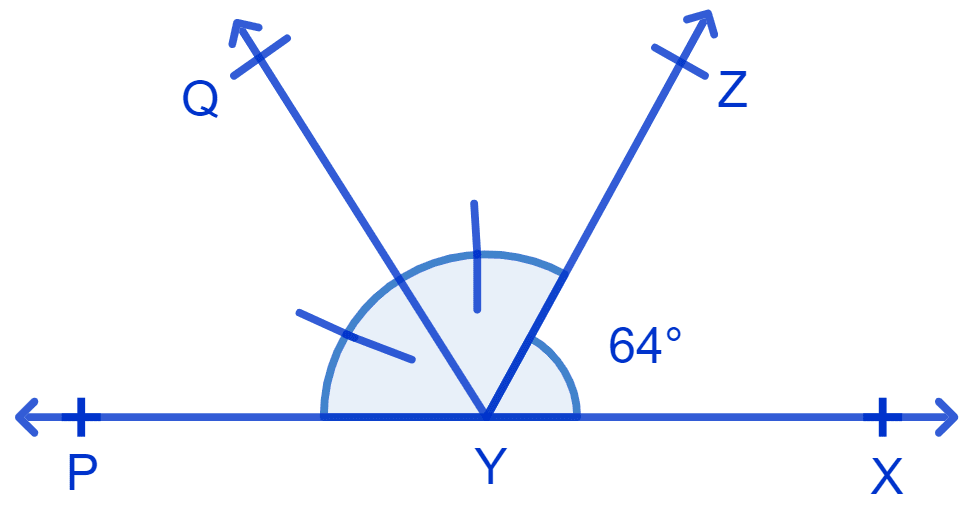
In the given figure,

Line YQ bisect ∠ZYP.

∴ ∠QYP = ∠ZYQ = x (let) .........(1)

From figure,

⇒ ∠XYZ + ∠ZYQ + ∠QYP = 180° [Linear pairs]

⇒ 64° + x + x = 180° [From equation (1)]

⇒ 64° + 2x = 180°

⇒ 2x = 180° - 64°

⇒ 2x = 116°

⇒ x = $\dfrac{116°}{2}$

⇒ x = 58°.

⇒ ∠ZYQ = ∠QYP = x = 58°

Reflex ∠QYP = 360° - ∠QYP = 360° - 58° = 302°.

From figure,

⇒ ∠XYQ = ∠XYZ + ∠ZYQ

= 64° + 58°

= 122°.

Hence, ∠XYQ = 122° and Reflex ∠QYP = 302°.

In Fig. if AB || CD, CD || EF and y : z = 3 : 7, find x.

Answer

It is given that y : z = 3 : 7

⇒ $\dfrac{y}{z} = \dfrac{3}{7}$

⇒ y = $\dfrac{3z}{7}$ ........(1)

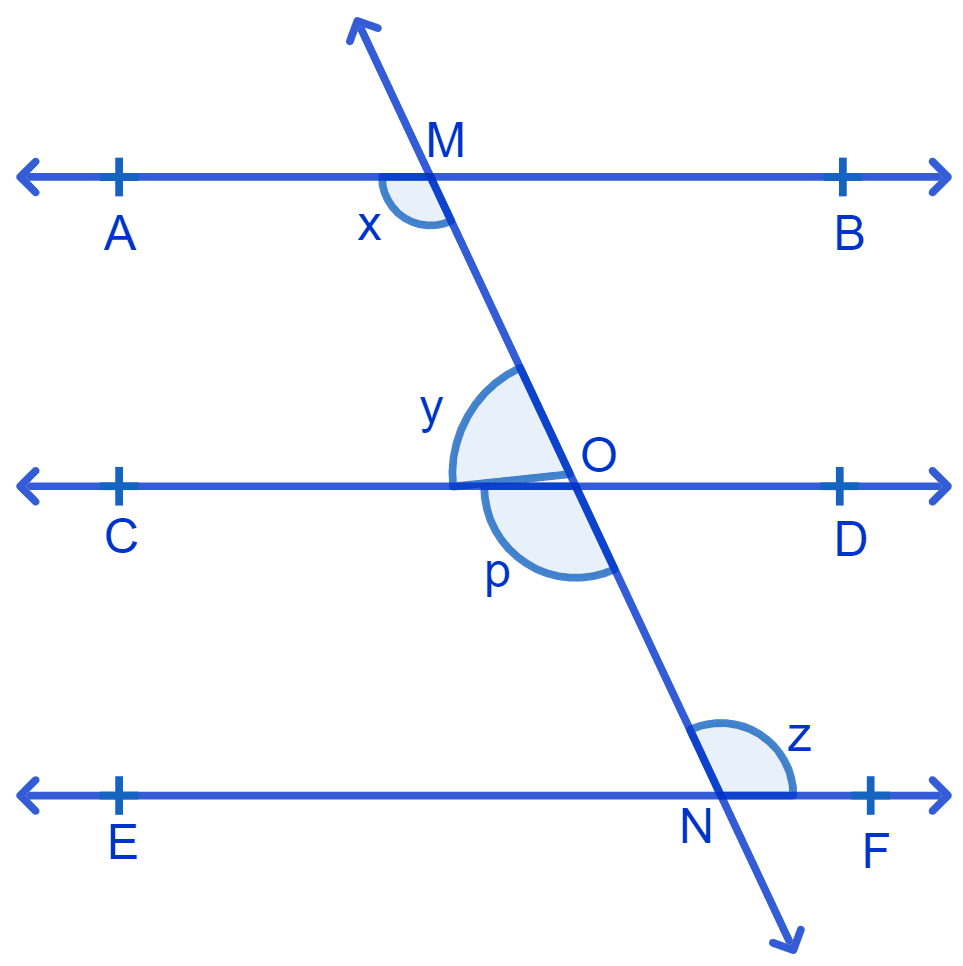
Let ∠CON = p

Since, CD || EF

∴ p = z (Alternate interior angles are equal) .....(2)

⇒ y + p = 180° (Linear pairs)

⇒ y + z = 180° [From (2)]

Substituting value of y from equation (1), in above equation, we get :

$\Rightarrow \dfrac{3z}{7} + z = 180° \\[1em] \Rightarrow \dfrac{3z + 7z}{7} = 180° \\[1em] \Rightarrow \dfrac{10z}{7} = 180° \\[1em] \Rightarrow z = \dfrac{7}{10} \times 180° \\[1em] \Rightarrow z = 126° \\[1em] \Rightarrow y = \dfrac{3}{7}z \\[1em] \Rightarrow y = \dfrac{3}{7} \times 126° \\[1em] \Rightarrow y = 3 \times 18° \\[1em] \Rightarrow y = 54°.$

From figure,

AB || CD & MN is transversal

We know that, the sum of co-interior angles are supplementary.

⇒ x + y = 180°

⇒ x + 54° = 180°

⇒ x = 180° - 54°

⇒ x = 126°

Hence, x = 126°.

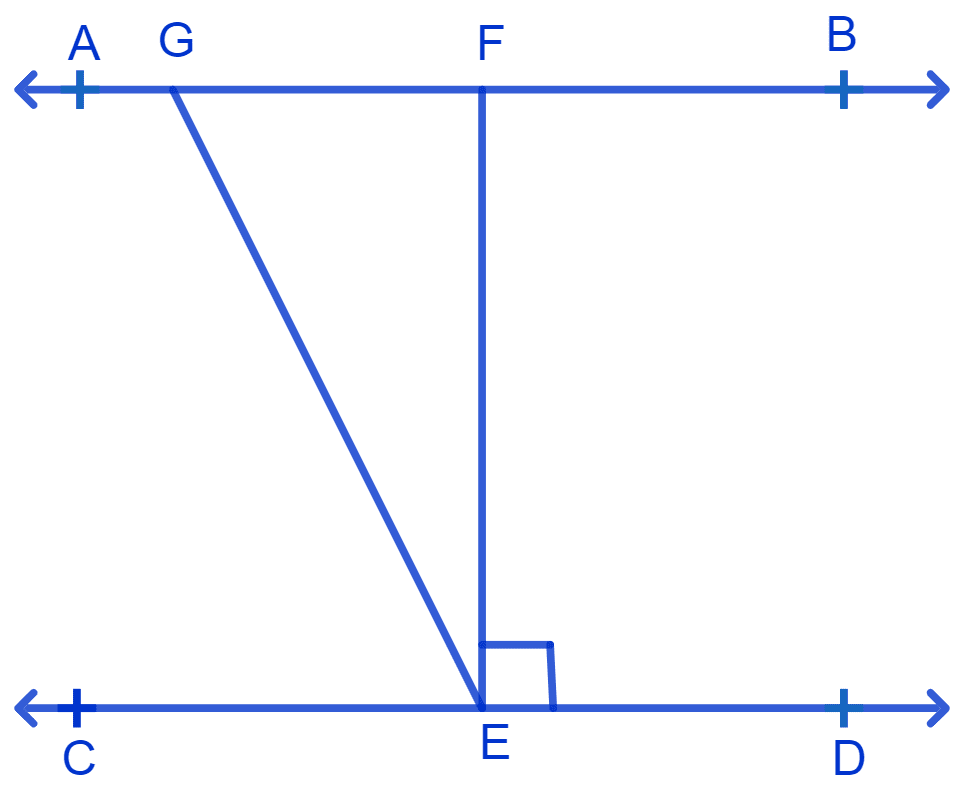
In Fig. if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.

Answer

Given :

AB || CD, ∠GED = 126°.

Since,

EF ⊥ CD.

∴ ∠FED = 90°.

From figure,

⇒ ∠GED = ∠GEF + ∠FED

⇒ ∠GEF = ∠GED - ∠FED

⇒ ∠GEF = 126° - 90°

⇒ ∠GEF = 36°.

AB and CD are parallel lines cut by a transversal GE, thus the pair of alternate interior angles formed are equal.

⇒ ∠AGE = ∠GED

⇒ ∠AGE = 126°.

From figure,

⇒ ∠AGE + ∠FGE = 180° [Linear pairs]

⇒ 126° + ∠FGE = 180°

⇒ ∠FGE = 180° - 126° = 54°.

Hence, ∠AGE = 126°, ∠GEF = 36° and ∠FGE = 54°.

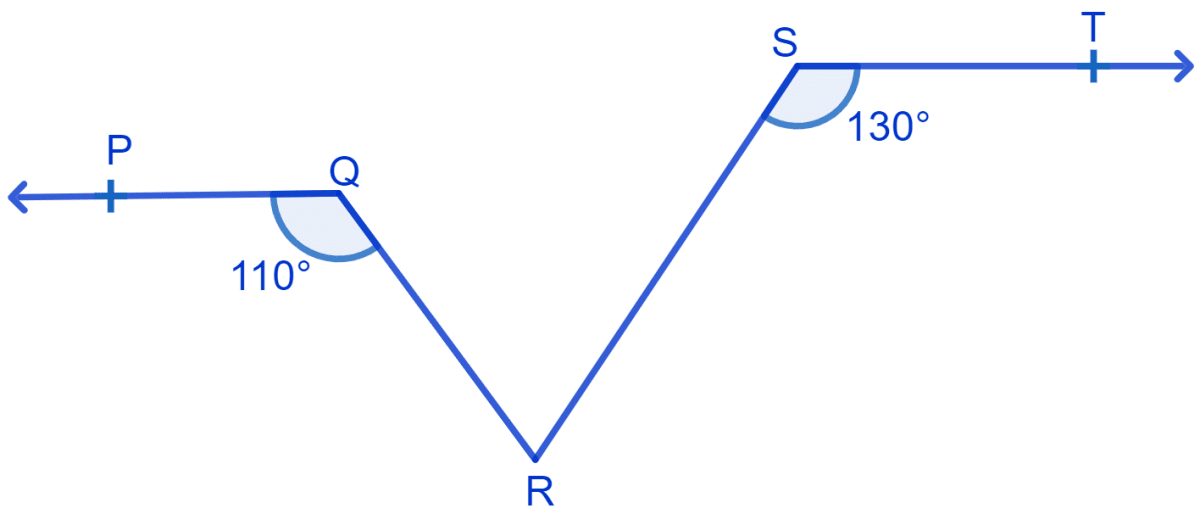
In Fig. if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.

Answer

It is given that PQ || ST,

Draw a line XY || ST,

So, XY || PQ, i.e, PQ || ST || XY

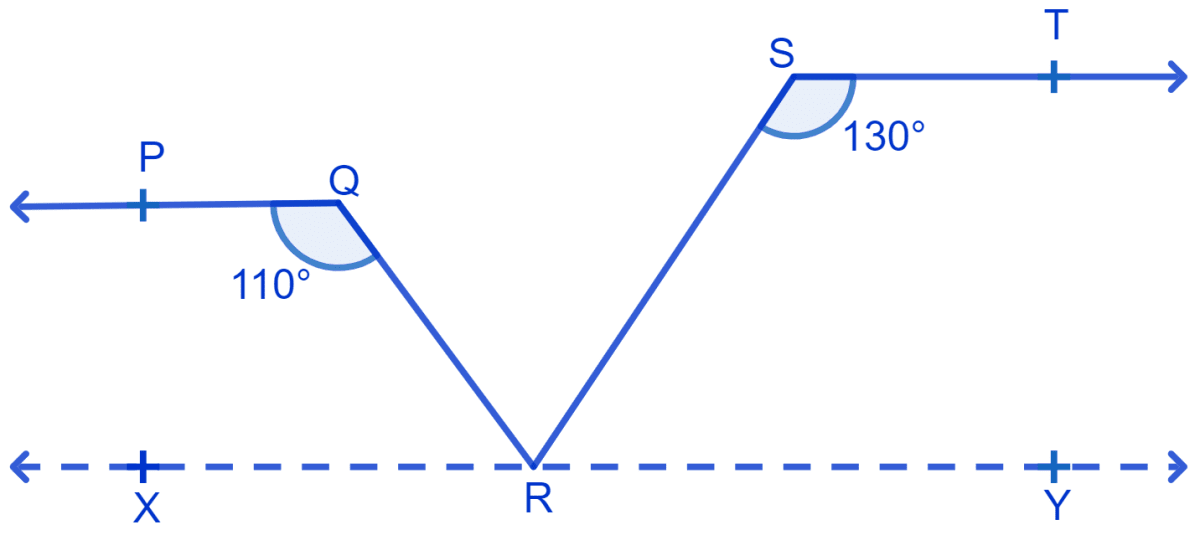
Since, PQ || XY & QR is the transversal.

We know that,

Sum of co-interior angles = 180°.

⇒ ∠PQR + ∠QRX = 180°

⇒ 110° + ∠QRX = 180°

⇒ ∠QRX = 180° - 110°

⇒ ∠QRX = 70°.

Also, ST || XY & SR is transversal

⇒ ∠SRY + ∠RST = 180° (Interior angles on the same side of the transversal are supplementary)

⇒ ∠SRY + 130° = 180°

⇒ ∠SRY = 180° - 130°

⇒ ∠SRY = 50°.

From figure,

⇒ ∠QRX + ∠QRS + ∠SRY = 180° (Linear pairs)

⇒ 70° + ∠QRS + 50° = 180°

⇒ 120° + ∠QRS = 180°

⇒ ∠QRS = 180° - 120°

⇒ ∠QRS = 60°

Hence, ∠QRS = 60°.

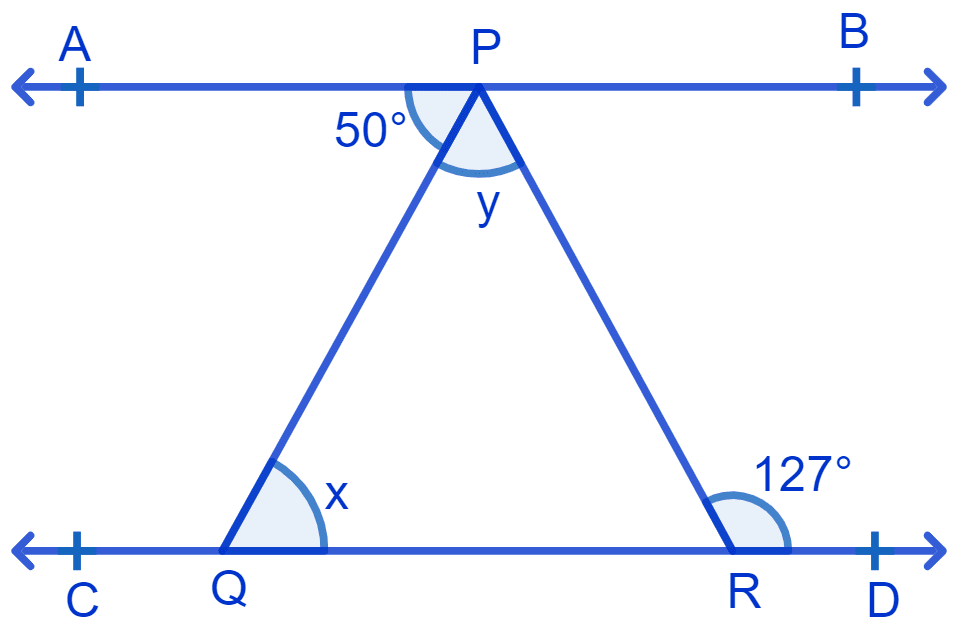
In Fig. if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

Answer

Given : ∠APQ = 50° and ∠PRD = 127°.

From figure,

PQ is the transversal.

⇒ ∠PQR = ∠APQ (Alternate interior angles are equal)

⇒ x = 50°.

From figure,

⇒ ∠PRQ + ∠PRD = 180° [Linear pairs]

⇒ ∠PRQ + 127° = 180°

⇒ ∠PRQ = 180° - 127° = 53°.

By angle sum property of triangle :

⇒ ∠PQR + ∠QPR + ∠PRQ = 180°

⇒ x + y + 53° = 180°

⇒ 50° + y + 53° = 180°

⇒ y = 180° - 103°

⇒ y = 77°

Hence, x = 50° and y = 77°.

In Fig. PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

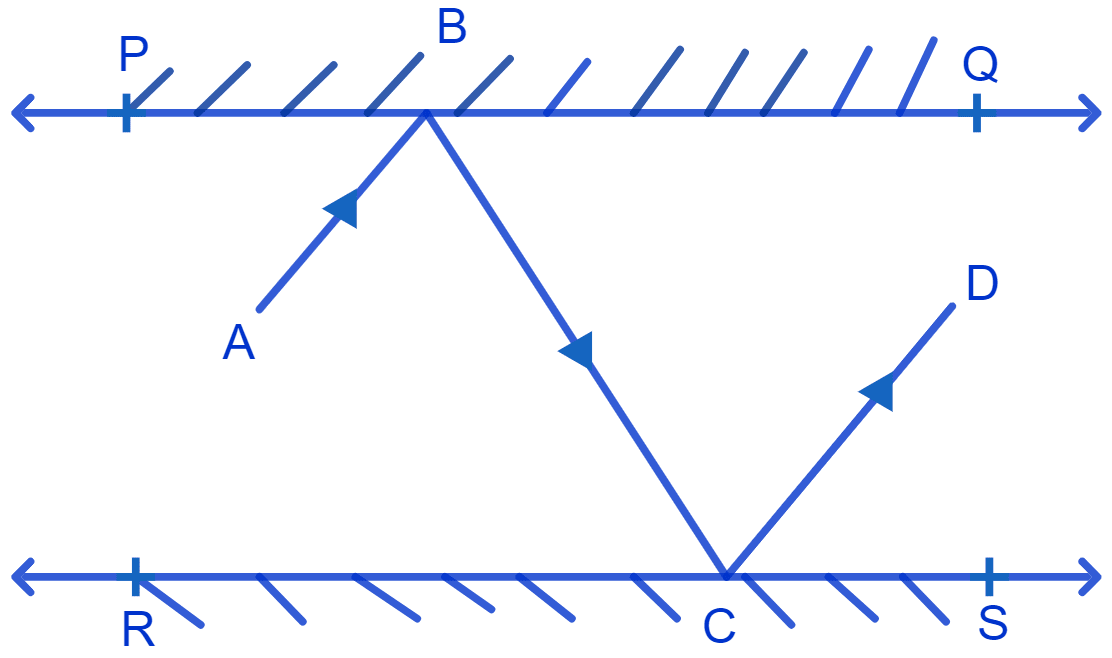
Answer

When two parallel lines are cut by a transversal, alternate angles formed are equal.

In optics the angle of incidence (the angle which an incident ray makes with a perpendicular to the surface at the point of incidence) and the angle of reflection (the angle formed by the reflected ray with a perpendicular to the surface at the point of incidence) are equal.

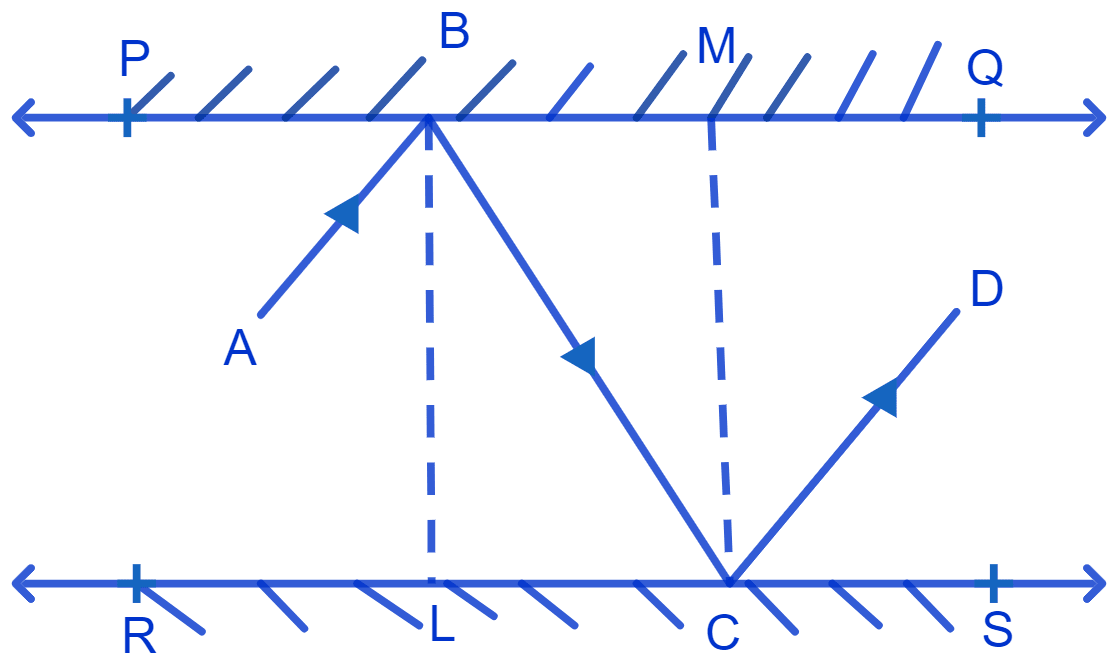
Draw a perpendicular line BL and CM at the point of incidence on both mirrors. Since PQ and RS are parallel to each other, perpendiculars drawn are also parallel i.e, BL || CM.

Since BC is a transversal to line BL and CM, alternate interior angles are equal.

∴ ∠LBC = ∠BCM = x .......(1)

By first law of reflection :

The angle of incidence (the angle which an incident ray makes with a perpendicular to the surface at the point of incidence) and the angle of reflection (the angle formed by the reflected ray with a perpendicular to the surface at the point of incidence) are equal.

By law of reflection, at the first point of incidence B on mirror PQ, we get :

⇒ ∠ABL = ∠LBC = x

⇒ ∠ABC = ∠ABL + ∠LBC

⇒ ∠ABC = x + x

⇒ ∠ABC = 2x ......(2)

By law of reflection, at the second point of incidence C on mirror RS, we get :

⇒ ∠MCD = ∠BCM = x

From figure,

⇒ ∠BCD = ∠BCM + ∠MCD

⇒ ∠BCD = x + x

⇒ ∠BCD = 2x .......(3)

From equation (2) and (3), we get ∠ABC = ∠BCD which are alternate interior angles for the lines AB and CD and BC as the transversal.

We know that, if a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.

Since, alternate interior angles are equal, we can say AB is parallel to CD (AB || CD).

Hence, proved that AB || CD.