Mathematics
Use the given figure to find :
(i) ∠BAD
(ii) ∠DQB.

Circles
12 Likes
Answer
(i) In △ADP,
⇒ ∠PAD + ∠ADP + ∠DPA = 180° [Angle sum property of triangle]
⇒ ∠PAD + 85° + 40° = 180°
⇒ ∠PAD + 125° = 180°
⇒ ∠PAD = 180° - 125° = 55°.
From figure,
⇒ ∠BAD = ∠PAD = 55°.
Hence, ∠BAD = 55°.
(ii) We know that,
Sum of opposite angles in a cyclic quadrilateral = 180°.
⇒ ∠ABC + ∠ADC = 180°
⇒ ∠ABC + 85° = 180°
⇒ ∠ABC = 180° - 85° = 95°.
In △AQB,
⇒ ∠AQB + ∠QAB + ∠ABQ = 180° [Angle sum property of triangle]
⇒ ∠AQB + ∠BAD + ∠ABC = 180° [From figure, ∠QAB = ∠BAD and ∠ABQ = ∠ABC]
⇒ ∠AQB + 55° + 95° = 180°
⇒ ∠AQB + 150° = 180°
⇒ ∠AQB = 180° - 150° = 30°.
From figure,
⇒ ∠DQB = ∠AQB = 30°.
Hence, ∠DQB = 30°.
Answered By
6 Likes
Related Questions
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.
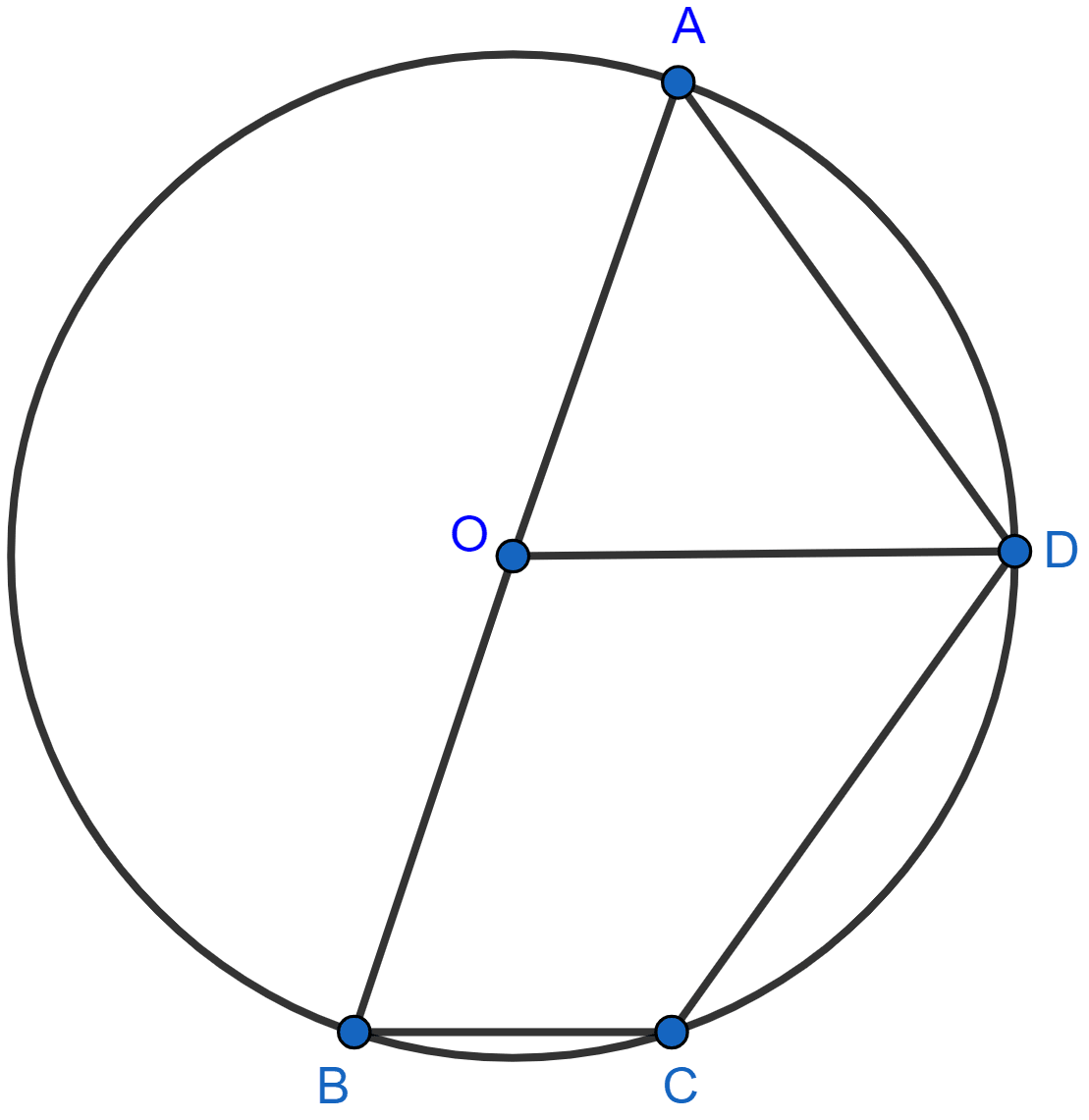
AB is the diameter of the circle with center O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
(i) ∠ABD,
(ii) ∠DBC,
(iii) ∠ADC.
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.

In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°, Calculate :
(i) ∠RPQ
(ii) ∠STP.
