Two isosceles triangles have equal vertical angles. Show that the triangles are similar.

If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.

Let △ABC and △PQR be two isosceles triangles with AB = AC and PQ = PR.

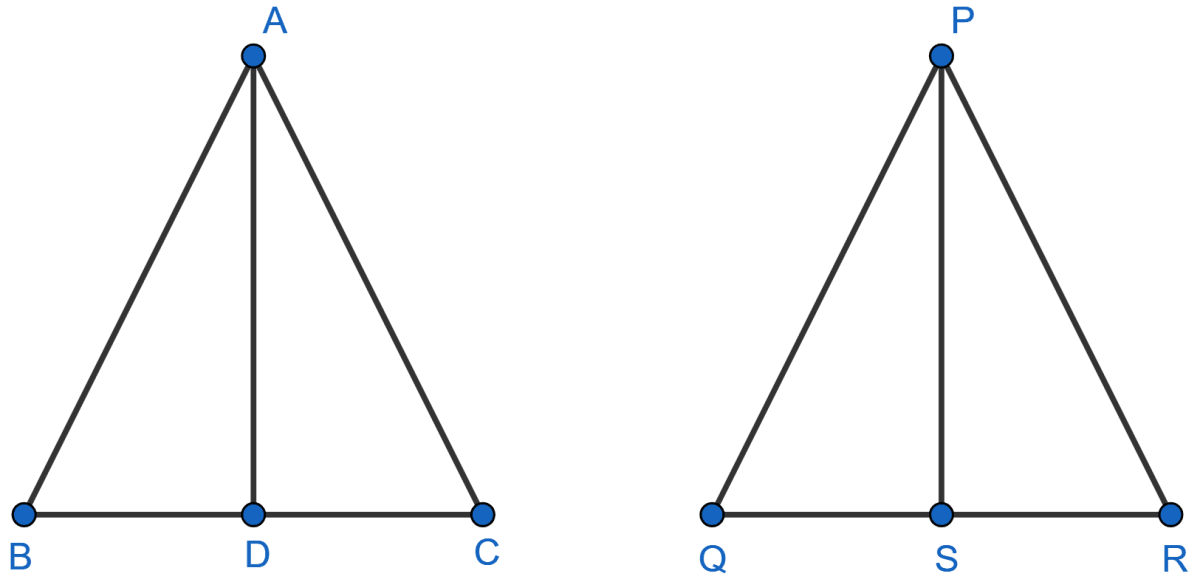
Then,

$\dfrac{AB}{AC} = \dfrac{PQ}{PR} = 1$.

or,

$\dfrac{AB}{PQ} = \dfrac{AC}{QR}$

Also,

∠A = ∠P (Given)

∴ △ABC ~ △PQR (By SAS)

We know that,

Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.

$\therefore\dfrac{\text{Area of ∆ABC}}{\text{Area of ∆PQR}} = \Big(\dfrac{AB}{PQ}\Big)^2 \\[1em] \Rightarrow \dfrac{16}{25} = \Big(\dfrac{AB}{PQ}\Big)^2 \\[1em] \Rightarrow \dfrac{AB}{PQ} = \sqrt{\dfrac{16}{25}} = \dfrac{4}{5}.$

We know that,

The ratio between sides of similar triangle is equal to ratio of their altitudes.

Hence, ratio between altitudes = 4 : 5.