Mathematics
A triangle ABC with AB = 3 cm, BC = 6 cm and AC = 4 cm is enlarged to △DEF such that the longest side of △DEF = 9 cm. Find the scale factor and hence, the lengths of the other sides of △DEF.
Similarity
8 Likes
Answer
Longest side in △ABC = BC = 6 cm
Corresponding longest side in △DEF = EF = 9 cm.
Scale factor (k) = = 1.5
Triangle ABC is enlarged to DEF. So, the two triangles will be similar.
.
So,
Hence, DE = 4.5 cm and DF = 6 cm.
Answered By
4 Likes
Related Questions
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find :
(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
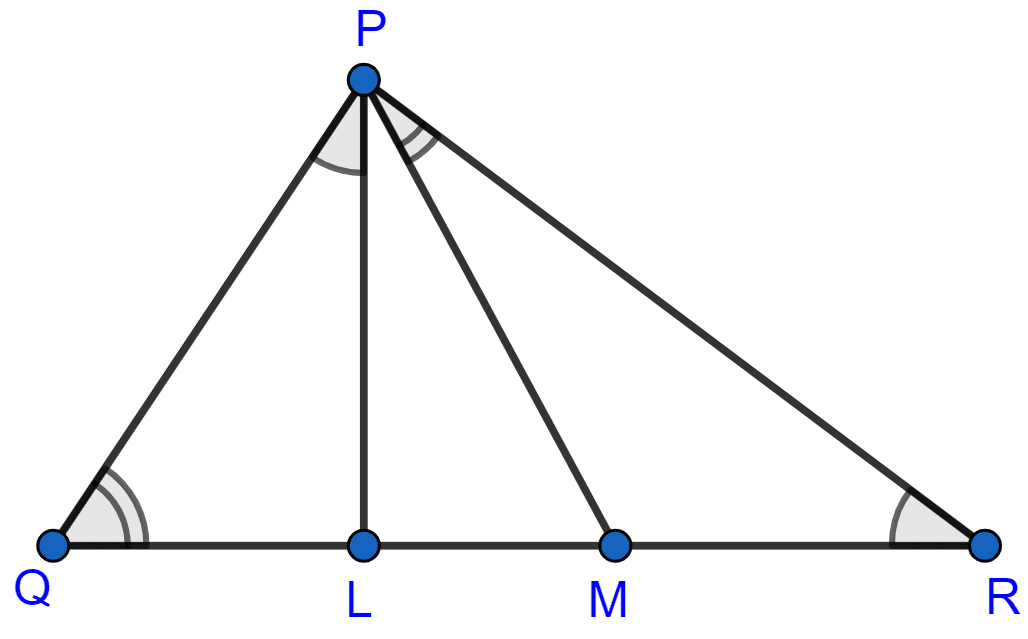
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that :
(i) △PQL ~ △RPM
(ii) QL × RM = PL × PM
(iii) PQ2 = QR × QL
Two isosceles triangles have equal vertical angles. Show that the triangles are similar.
If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
In △ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find :
(i) area △APO : area △ABC
(ii) area △APO : area △CQO.
