Mathematics
In the given figure, ABC is a triangle with ∠EDB = ∠ACB. Prove that △ABC ~ △EBD. If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of △BED = 9 cm2. Calculate the :
(i) length of AB
(ii) area of △ABC

Similarity
13 Likes
Answer
(i) In △ABC and △EBD,
⇒ ∠EDB = ∠ACB [Given]
⇒ ∠DBE = ∠ABC [Common]
∴ △ABC ~ △EBD
From figure,
⇒ BC = BE + EC = 6 + 4 = 10 cm.
Since, corresponding sides of similar triangles are proportional to each other.
Hence, length of AB = 12 cm.
(ii) We know that,
Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.
Hence, area of ∆ABC = 36 cm2.
Answered By
8 Likes
Related Questions
Two isosceles triangles have equal vertical angles. Show that the triangles are similar.
If the ratio between the areas of these two triangles is 16 : 25, find the ratio between their corresponding altitudes.
In △ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find :
(i) area △APO : area △ABC
(ii) area △APO : area △CQO.

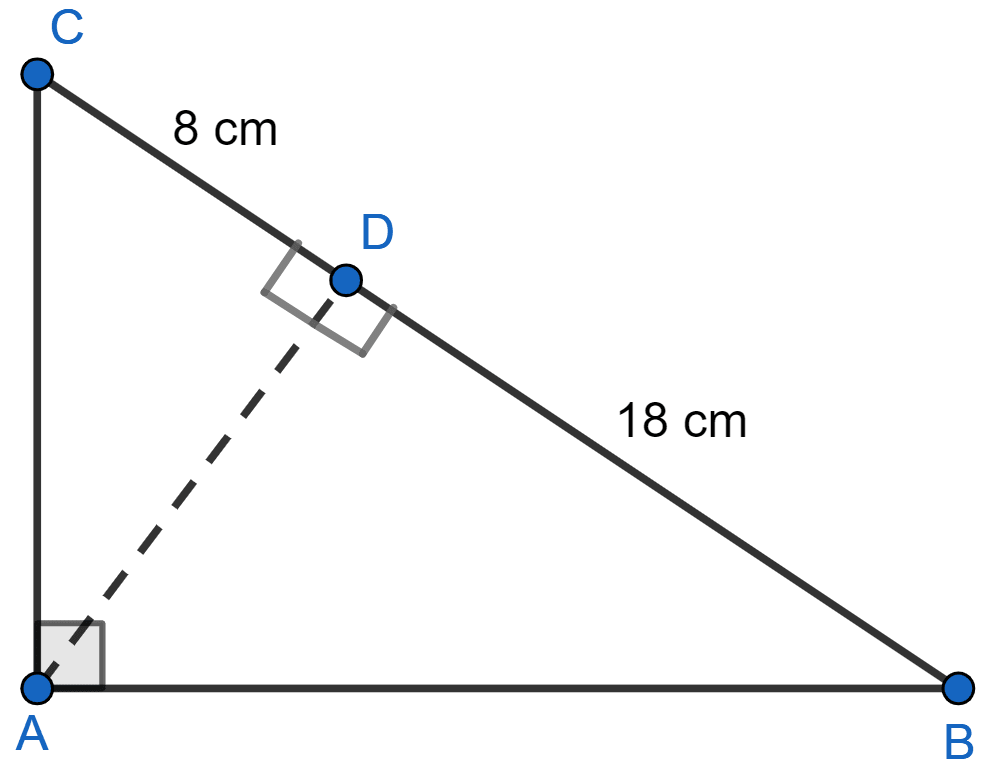
In the given figure, ABC is a right angled triangle with ∠BAC = 90°.
(i) Prove that : △ADB ~ △CDA.
(ii) If BD = 18 cm and CD = 8 cm, find AD.
(iii) Find the ratio of the area of △ADB is to area of △CDA.
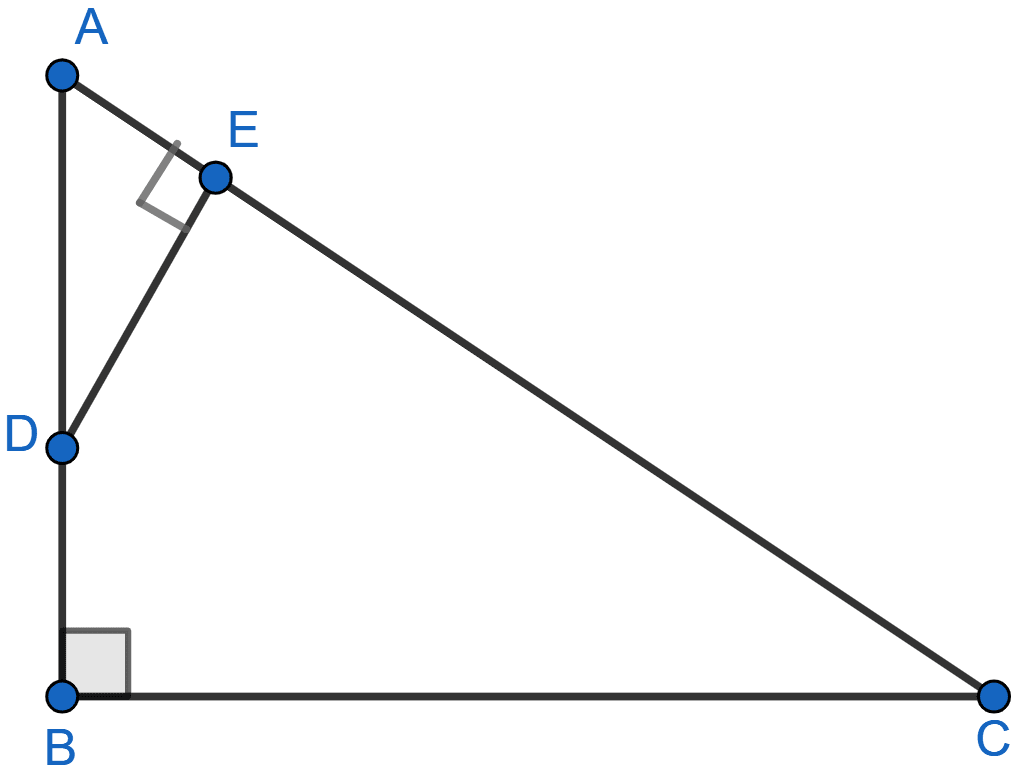
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
(i) △ADE ~ △ACB
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of △ADE : area of quadrilateral BCED.