Mathematics
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their:
(i) corresponding medians.
(ii) perimeters.
(iii) areas.
Similarity
3 Likes
Answer
Let △ABC and △PQR be two similar triangles with AD and PS as perpendiculars.
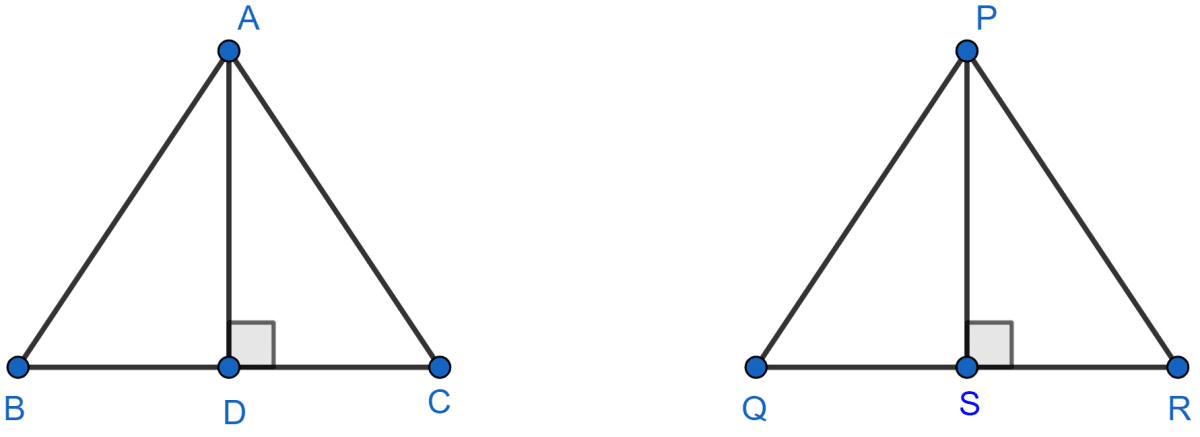
So,
∠ABD = ∠PQS [As ∠ABC = ∠PQR]
∠ADB = ∠PSQ [Both = 90°]
So, △ABD ~ △PQS.
.
(i) The ratio between the medians of two similar triangles is same as the ratio between their sides.
Hence, the required ratio = 3 : 5.
(ii) The ratio between the perimeters of two similar triangles is same as the ratio between their sides.
Hence, the required ratio = 3 : 5.
(iii) The ratio between the areas of two similar triangles is same as the square of the ratio between their corresponding sides.
Ratio = (3)2 : (5)2 = 9 : 25.
Hence, the required ratio = 9 : 25.
Answered By
1 Like
Related Questions
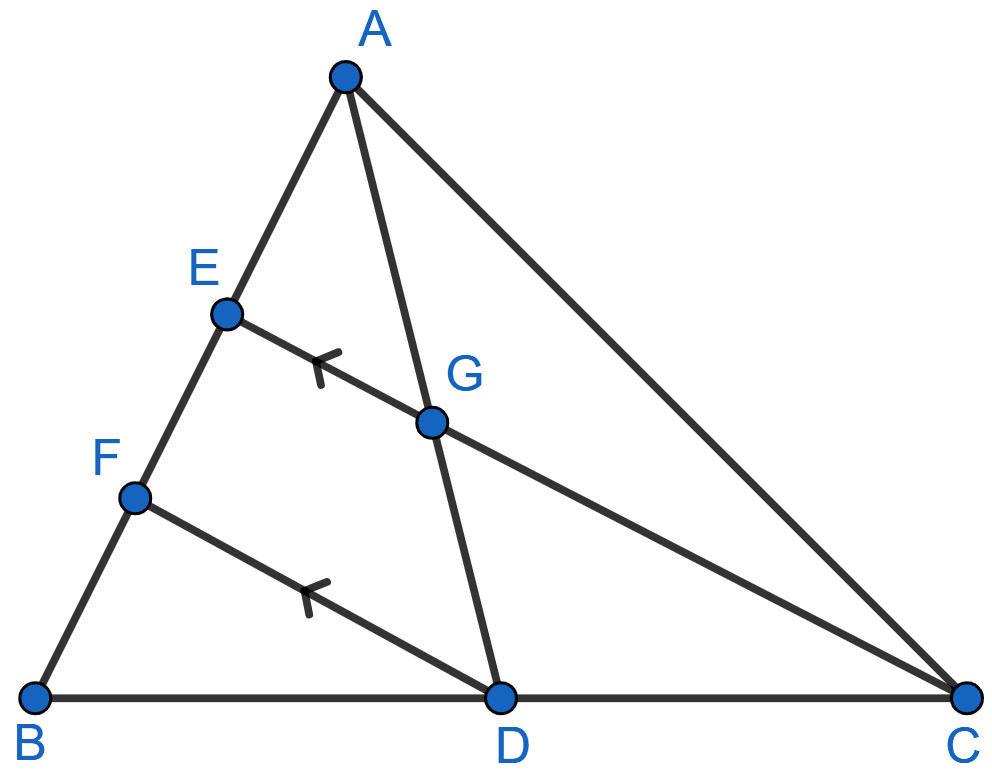
In the following figure, AD and CE are medians of ∆ABC. DF is drawn parallel to CE. Prove that:
(i) EF = FB,
(ii) AG : GD = 2 : 1
The two similar triangles are equal in area. Prove that the triangles are congruent.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
(i) perimeters
(ii) corresponding altitudes
(iii) corresponding medians.
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
(i) the diagonal distance of the plot in kilometre.
(ii) the area of the plot in sq. km.