Mathematics
The two similar triangles are equal in area. Prove that the triangles are congruent.
Similarity
4 Likes
Answer
Let's consider two similar triangles as ∆ABC ~ ∆PQR
We know that,
The areas of two similar triangles are proportional to the squares of their corresponding sides.
So,
Since,
Area of ∆ABC = Area of ∆PQR [Given]
Hence,
AB = PQ
BC = QR
AC = PR
So, as the respective sides of two similar triangles are all of same length.
We can conclude that,
∆ABC ≅ ∆PQR [By SSS rule]
Hence proved that both triangles are congruent.
Answered By
3 Likes
Related Questions
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(i) Prove that ΔACD is similar to ΔBCA.
(ii) Find BC and CD.
(iii) Find the area of ΔACD : area of ΔABC.
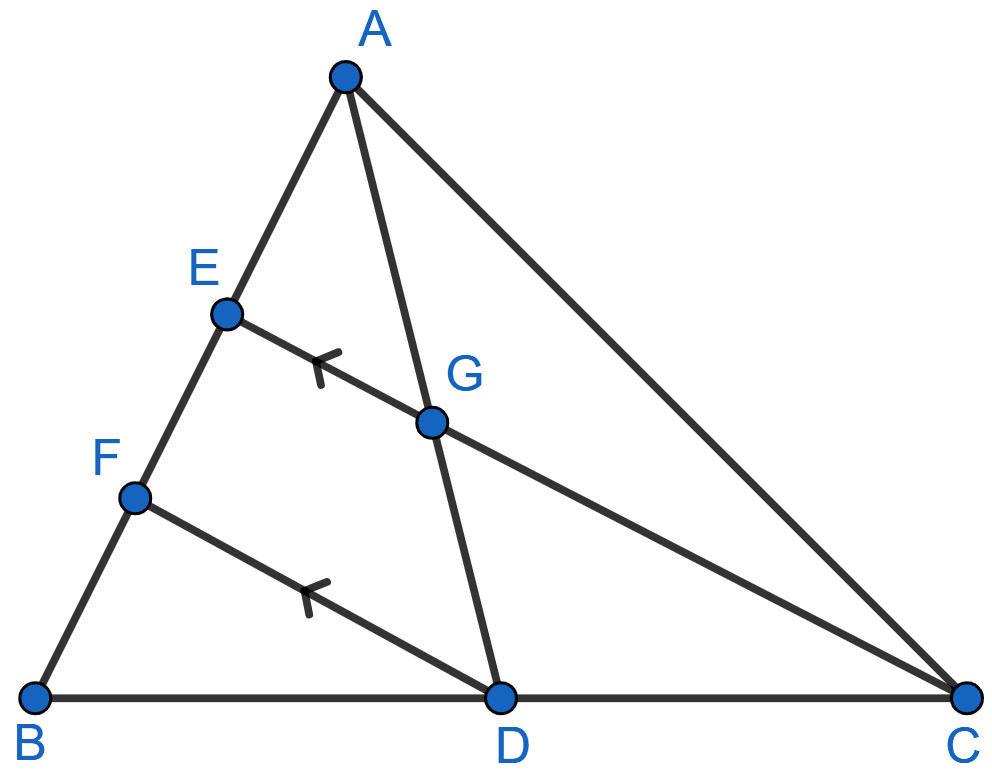
In the following figure, AD and CE are medians of ∆ABC. DF is drawn parallel to CE. Prove that:
(i) EF = FB,
(ii) AG : GD = 2 : 1
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their:
(i) corresponding medians.
(ii) perimeters.
(iii) areas.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
(i) perimeters
(ii) corresponding altitudes
(iii) corresponding medians.