Mathematics
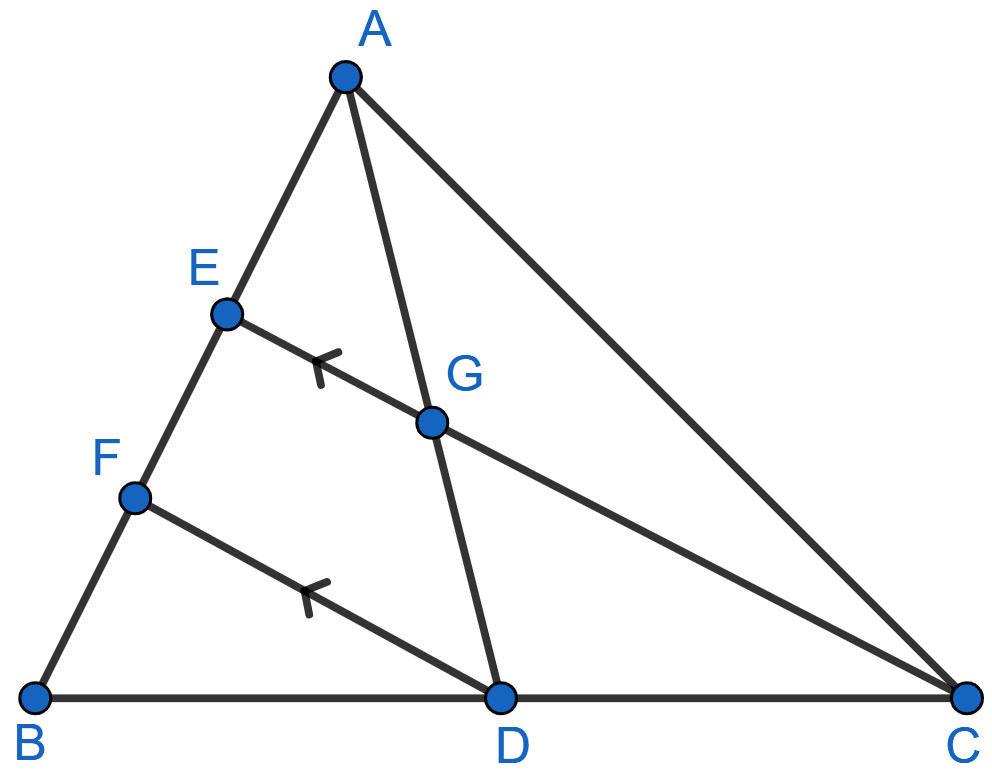
In the following figure, AD and CE are medians of ∆ABC. DF is drawn parallel to CE. Prove that:
(i) EF = FB,
(ii) AG : GD = 2 : 1
Similarity
32 Likes
Answer
(i) In ∆BFD and ∆BEC,
∠BFD = ∠BEC [Corresponding angles are equal]
∠FBD = ∠EBC [Common]
∴ ∆BFD ~ ∆BEC [By AA].
Since, corresponding sides of similar triangles are proportional.
[∵ AD is median so D is the mid-point of BC]
From figure,
⇒ BE = BF + FE
⇒ 2BF = BF + FE
⇒ BF = FE.
Hence, proved that EF = FB.
(ii) In ∆AFD, EG || FD.
By basic proportionality theorem we have,
…..(1)
Now, AE = EB [∵ CE is median so E is the mid-point of AB]
As, AE = EB = 2EF [As, EF = FB].
Substituting value of AE in (1) we get,
.
Hence, AG : GD = 2 : 1.
Answered By
19 Likes
Related Questions
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate: (i) EF (ii) AC

In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(i) Prove that ΔACD is similar to ΔBCA.
(ii) Find BC and CD.
(iii) Find the area of ΔACD : area of ΔABC.
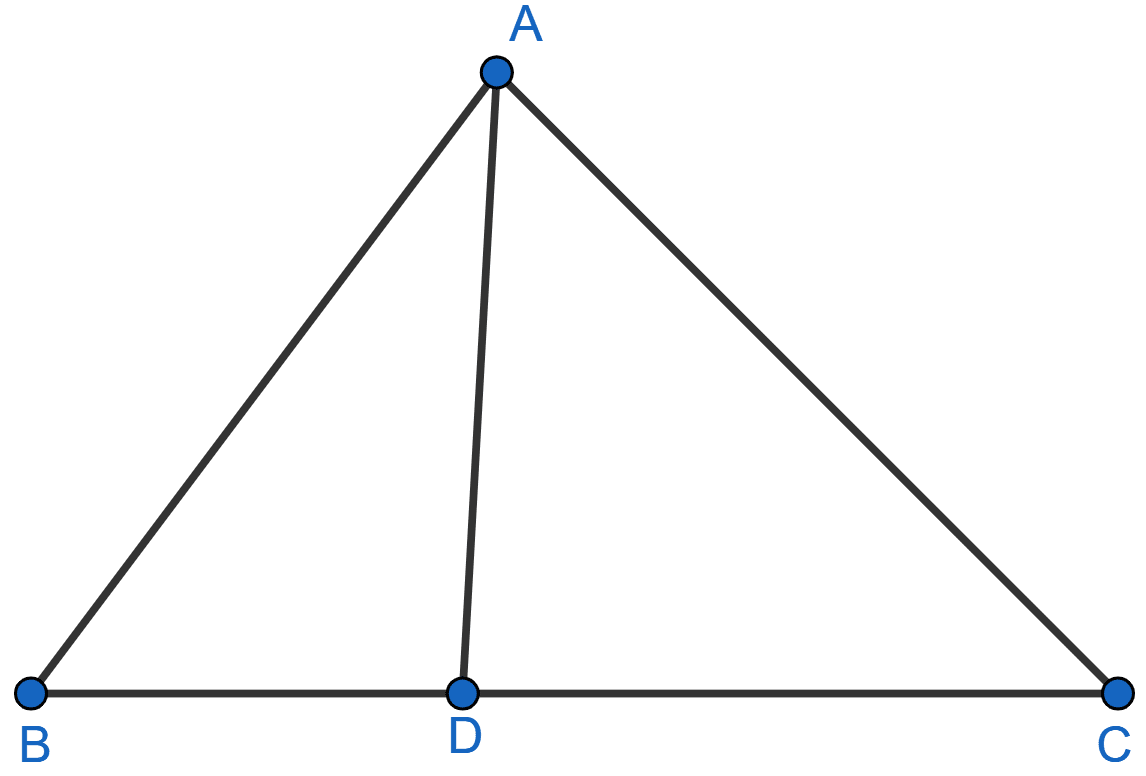
The two similar triangles are equal in area. Prove that the triangles are congruent.
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their:
(i) corresponding medians.
(ii) perimeters.
(iii) areas.