Mathematics
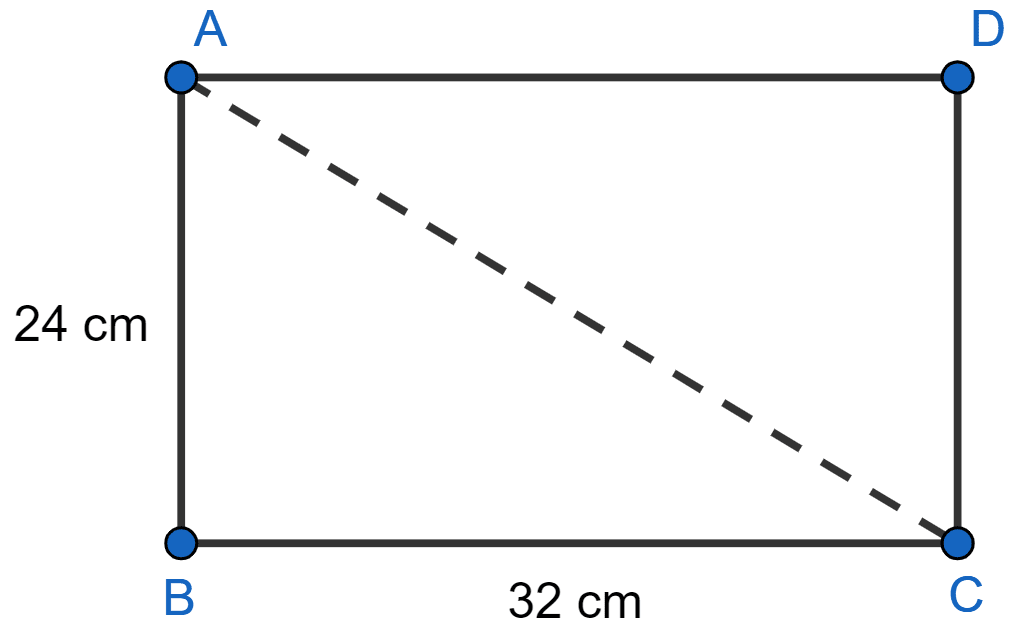
On a map, drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 24 cm and BC = 32 cm. Calculate :
(i) the diagonal distance of the plot in kilometre.
(ii) the area of the plot in sq. km.
Similarity
16 Likes
Answer
The rectangular plot of land ABCD on the map is shown below:
(i) By pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 242 + 322
⇒ AC2 = 576 + 1024
⇒ AC2 = 1600
⇒ AC = = 40 cm.
Given,
Scale (k) =
Length of diagonal distance in map = k × Length of diagonal of plot
40 = × Length of diagonal of plot
Length of diagonal of plot = 40 × 20000 = 800000 cm = km = 8 km.
Hence, diagonal distance of plot = 8 km.
(ii) Area of plot on map = AB × BC = 24 × 32 = 768 cm2.
Area of plot on map = k2 × Area of actual plot
768 = × Area of actual plot
Area of actual plot = 768 × 20000 × 20000 cm2
= km2
= 30.72 km2.
Hence, area of plot = 30.72 km2.
Answered By
12 Likes
Related Questions
The ratio between the altitudes of two similar triangles is 3 : 5; write the ratio between their:
(i) corresponding medians.
(ii) perimeters.
(iii) areas.
The ratio between the areas of two similar triangles is 16 : 25. State the ratio between their :
(i) perimeters
(ii) corresponding altitudes
(iii) corresponding medians.
The dimensions of the model of a multistoreyed building are 1 m by 60 cm by 1.20 m. If the scale factor is 1 : 50, find the actual dimensions of the building.
Also, find :
(i) the floor area of a room of the building, if the floor area of the corresponding room in the model is 50 sq. cm.
(ii) the space (volume) inside a room of the model, if the space inside the corresponding room of the building is 90 m3.
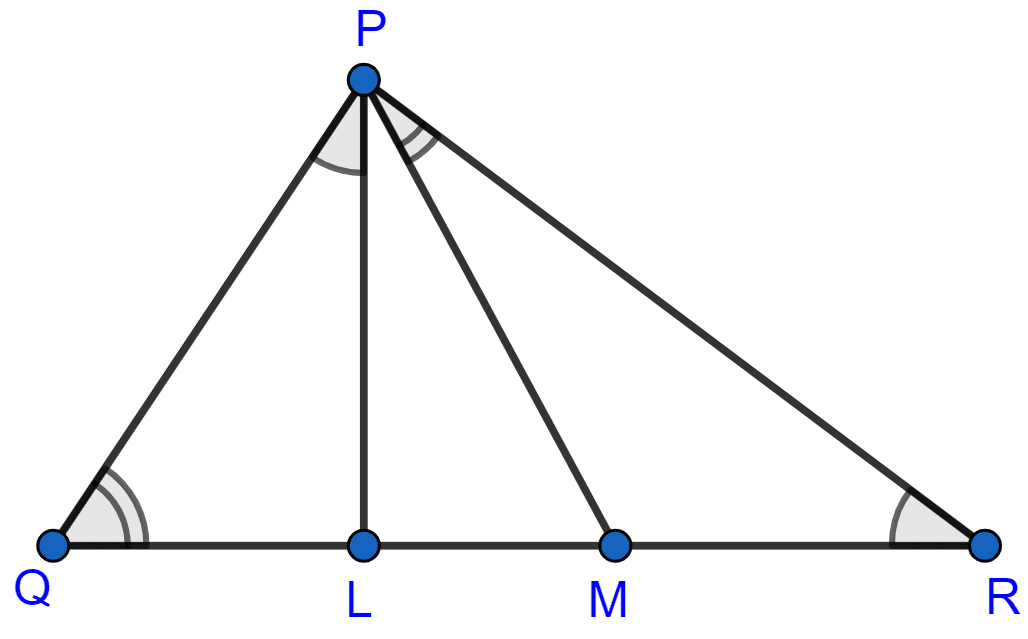
In a triangle PQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that :
(i) △PQL ~ △RPM
(ii) QL × RM = PL × PM
(iii) PQ2 = QR × QL