Mathematics
The lower window of a house is at height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At a certain instant, the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
Heights & Distances
1 Like
Answer
Let A be the position of balloon, F be the lower window and G be the upper window.
EF = 2 m and FG = 4 m
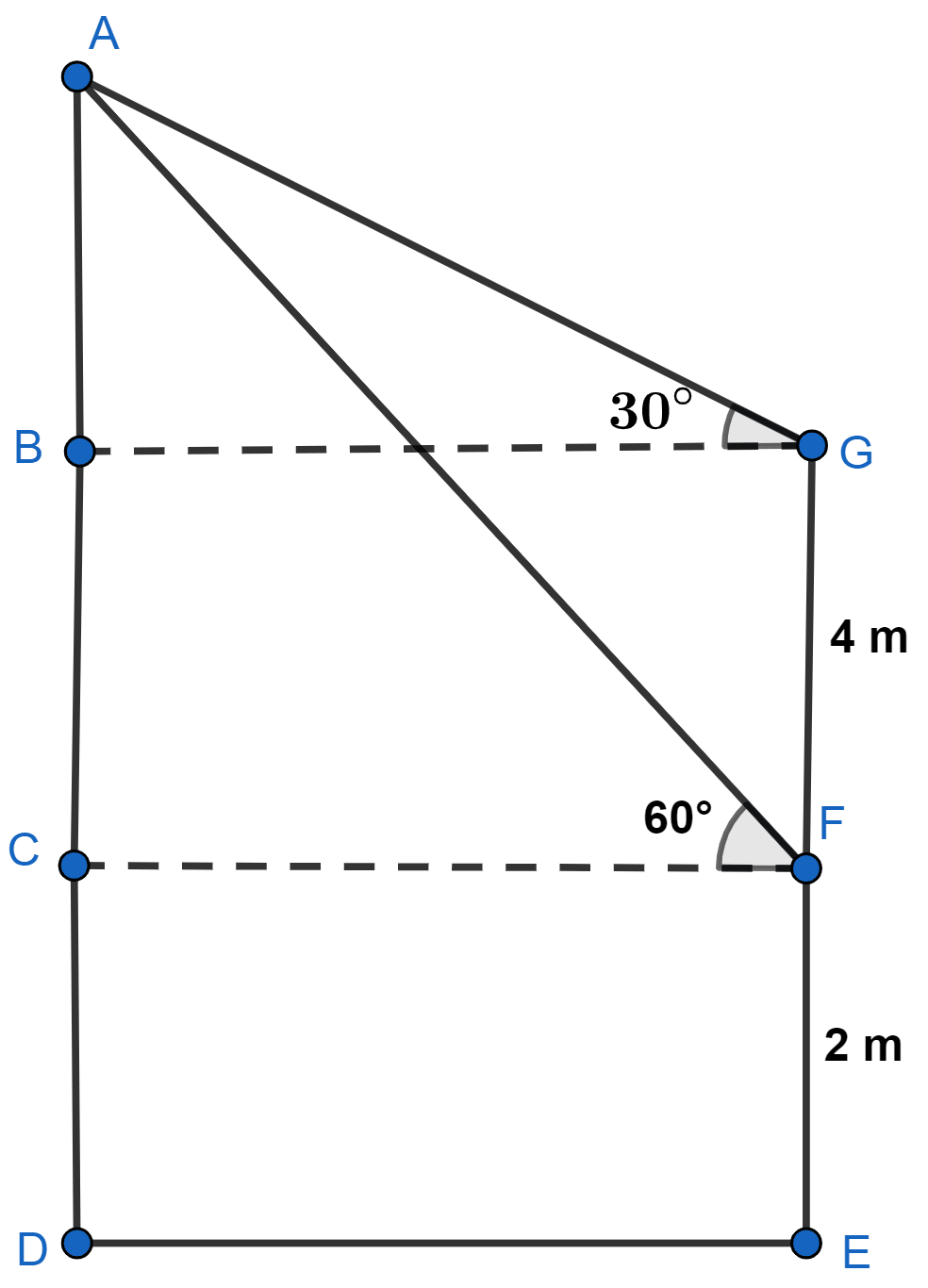
From figure,
BG = CF = x (let)
BC = FG = 4 m
In △ABG,
In △ACF,
From (1) and (2), we get :
From figure,
AD = AB + BC + CD = 2 m + 4 m + 2 m = 8 m.
Hence, height of balloon above the ground is 8 m.
Answered By
2 Likes
Related Questions
The sides of a right-angled triangle, containing the right angle, are 3(x + 1) cm and (2x - 1) cm. If the area of the triangle is 30 cm2, find the lengths of the sides of the triangle.
The daily wages of 160 workers in a factory are given below :
Wages (in ₹) No. of workers 50-60 12 60-70 20 70-80 30 80-90 38 90-100 24 100-110 16 110-120 12 120-130 8 Draw a cumulative frequency curve and estimate :
(i) median wage
(ii) inter-quartile range
(iii) percentage of workers who earn more than ₹ 95 per day.
Solve for x : .
Construct a triangle PQR, in which PR = 6 cm ad PQ = QR = 6.8 cm.
(i) Mark S the mid-point of PQ.
(ii) Construct the circle which touches QR at R and passes through S.