Mathematics
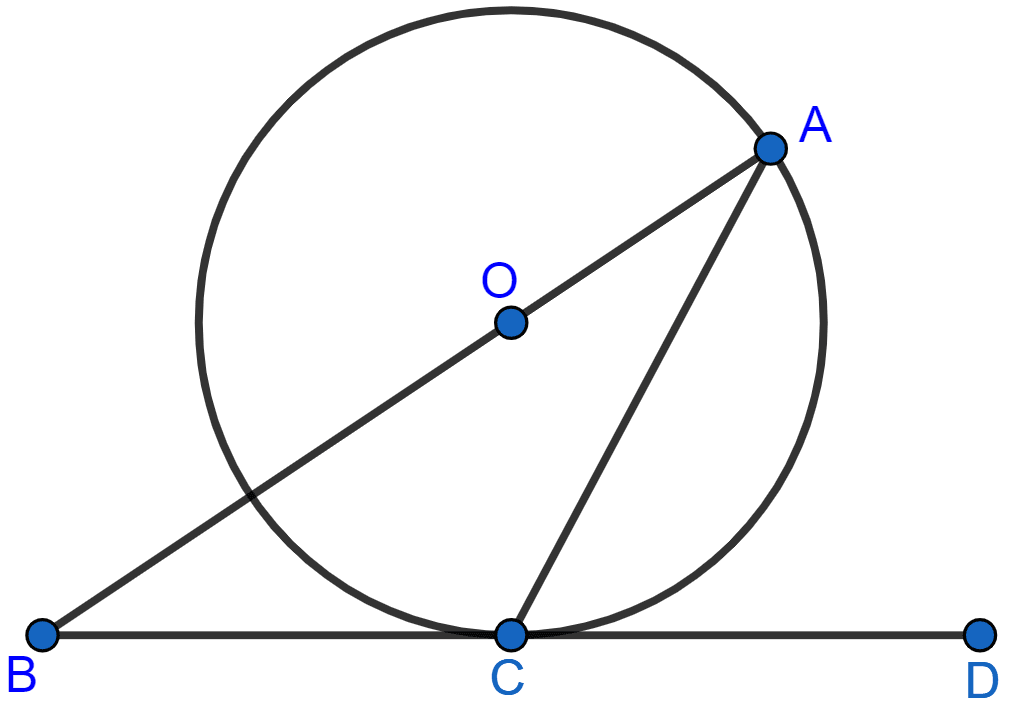
The given figure shows a circle with centre O and BCD is a tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.
Answer
Join OC.
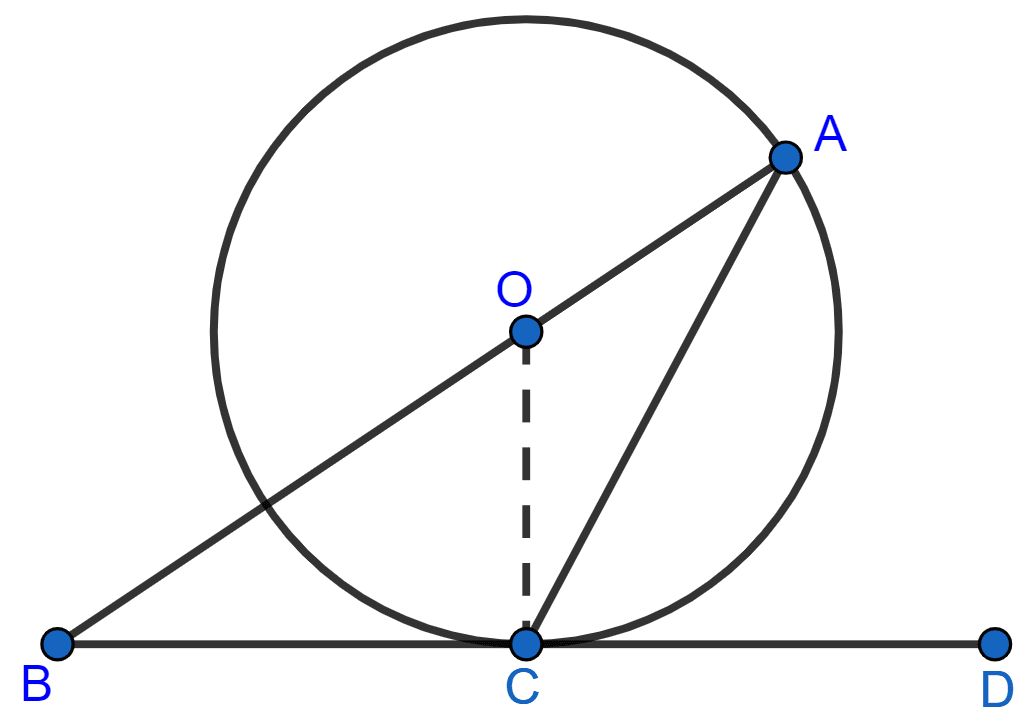
We know that,
The radius from the center of the circle to the point of tangent is perpendicular to the tangent line.
BCD is the tangent and OC is the radius.
As, OC ⊥ BD
∠OCD = 90°
∴ ∠OCA + ∠ACD = 90° …………. (1)
In ∆OCA,
⇒ OA = OC [Radius of the same circle]
∴ ∠OCA = ∠OAC [As, angles opposite to equal sides are equal]
Substituting in (1), we get
⇒ ∠OAC + ∠ACD = 90°
⇒ ∠BAC + ∠ACD = 90° [From figure, ∠BAC = ∠OAC]
Hence, proved that ∠ACD + ∠BAC = 90°.
Related Questions
P is the midpoint of an arc APB of a circle. Prove that the tangent drawn at P will be parallel to the chord AB.
ABC is a right triangle with angle B = 90°. A circle with BC as diameter meets hypotenuse AC at point D. Prove that:
(i) AC x AD = AB2
(ii) BD2 = AD x DC.
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find:
(i) ∠DBC
(ii) ∠BCP
(iii) ∠ADB

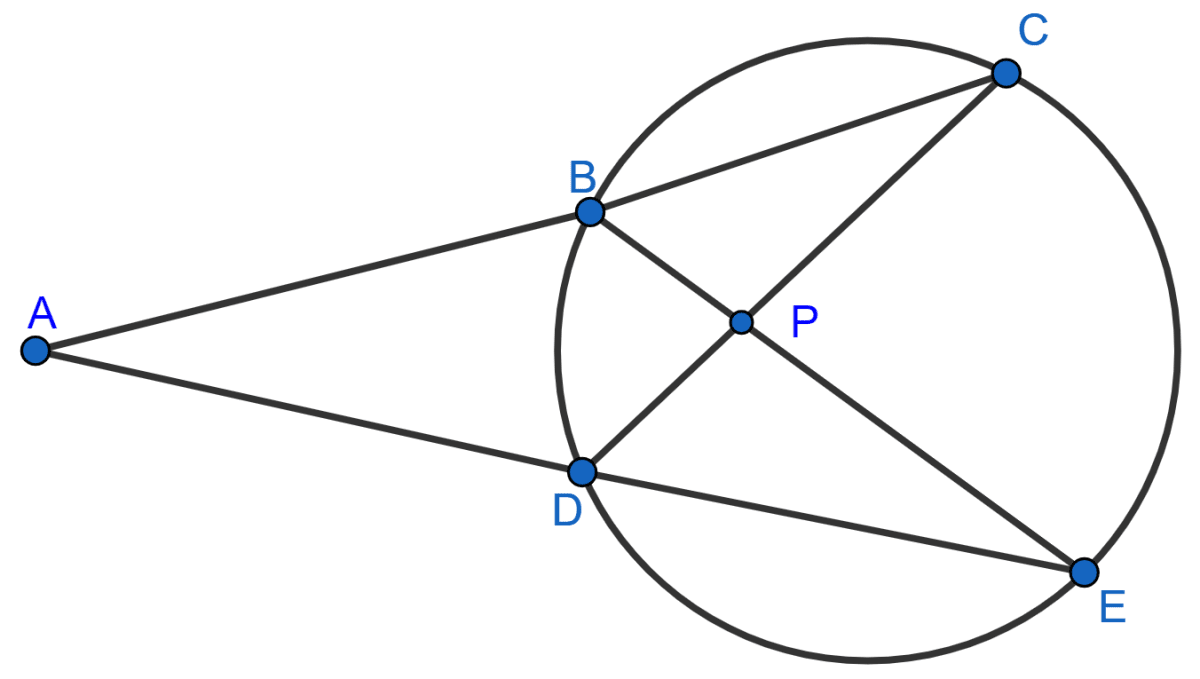
In the given figure, AC = AE.
Show that :
(i) CP = EP
(ii) BP = DP