Mathematics
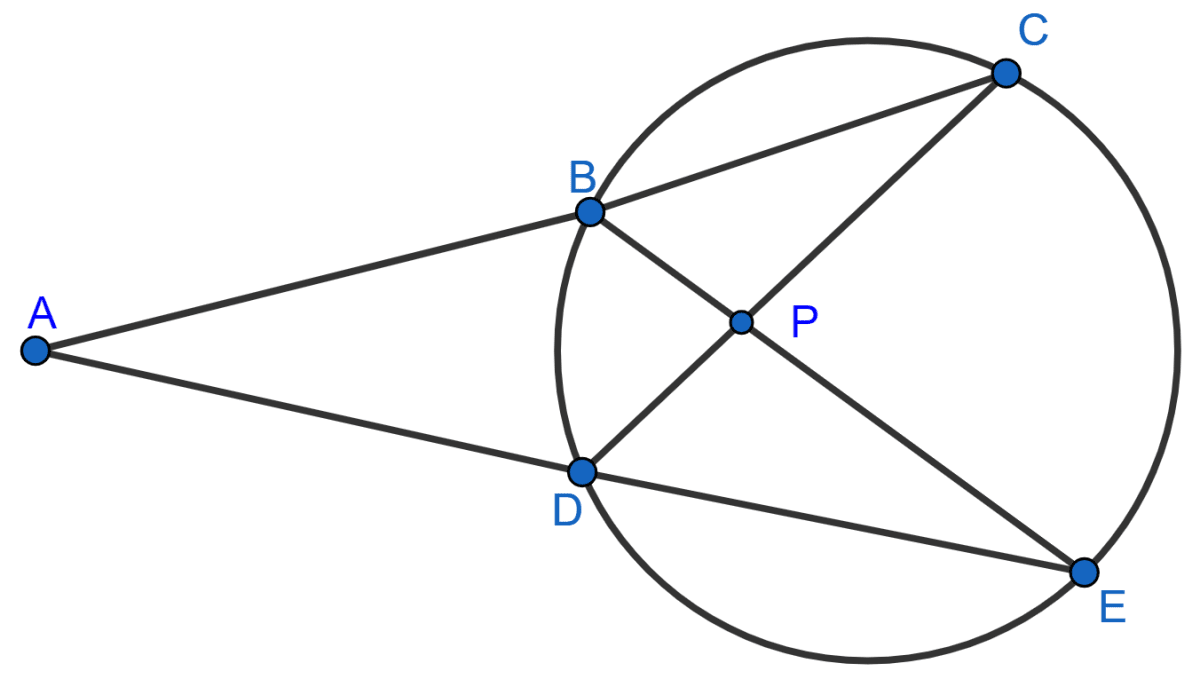
In the given figure, AC = AE.
Show that :
(i) CP = EP
(ii) BP = DP
Circles
4 Likes
Answer
(i) In ∆ADC and ∆ABE,
⇒ ∠ACD = ∠AEB [Angles in the same segment are equal]
⇒ AC = AE [Given]
⇒ ∠A = ∠A [Common]
Hence, ∆ADC ≅ ∆ABE by ASA axiom.
So, by C.P.C.T we have
⇒ AD = AB …………..(1)
Given,
⇒ AE = AC ………….(2)
Subtracting equation (1) from (2), we get :
⇒ AE - AD = AC - AB
⇒ DE = BC
In ∆BPC and ∆DPE,
⇒ ∠C = ∠E [Angles in the same segment are equal]
⇒ BC = DE [Proved above]
⇒ ∠CBP = ∠PDE [Angles in the same segment are equal]
Hence, ∆BPC ≅ ∆DPE by ASA axiom.
So, by C.P.C.T we have
⇒ CP = EP
Hence, proved that CP = EP.
(ii) Proved above,
∆BPC ≅ ∆DPE
∴ BP = DP [By C.P.C.T]
Hence, proved that BP = DP.
Answered By
3 Likes
Related Questions
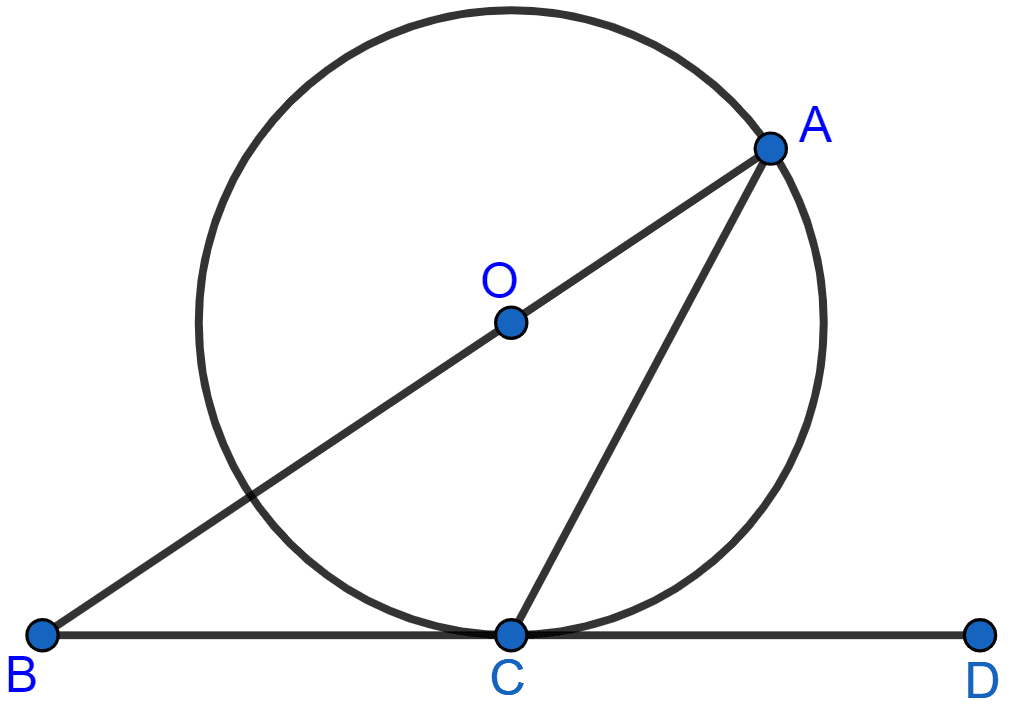
The given figure shows a circle with centre O and BCD is a tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.
ABC is a right triangle with angle B = 90°. A circle with BC as diameter meets hypotenuse AC at point D. Prove that:
(i) AC x AD = AB2
(ii) BD2 = AD x DC.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate :
(i) ∠BEC
(ii) ∠BED
In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
