Mathematics
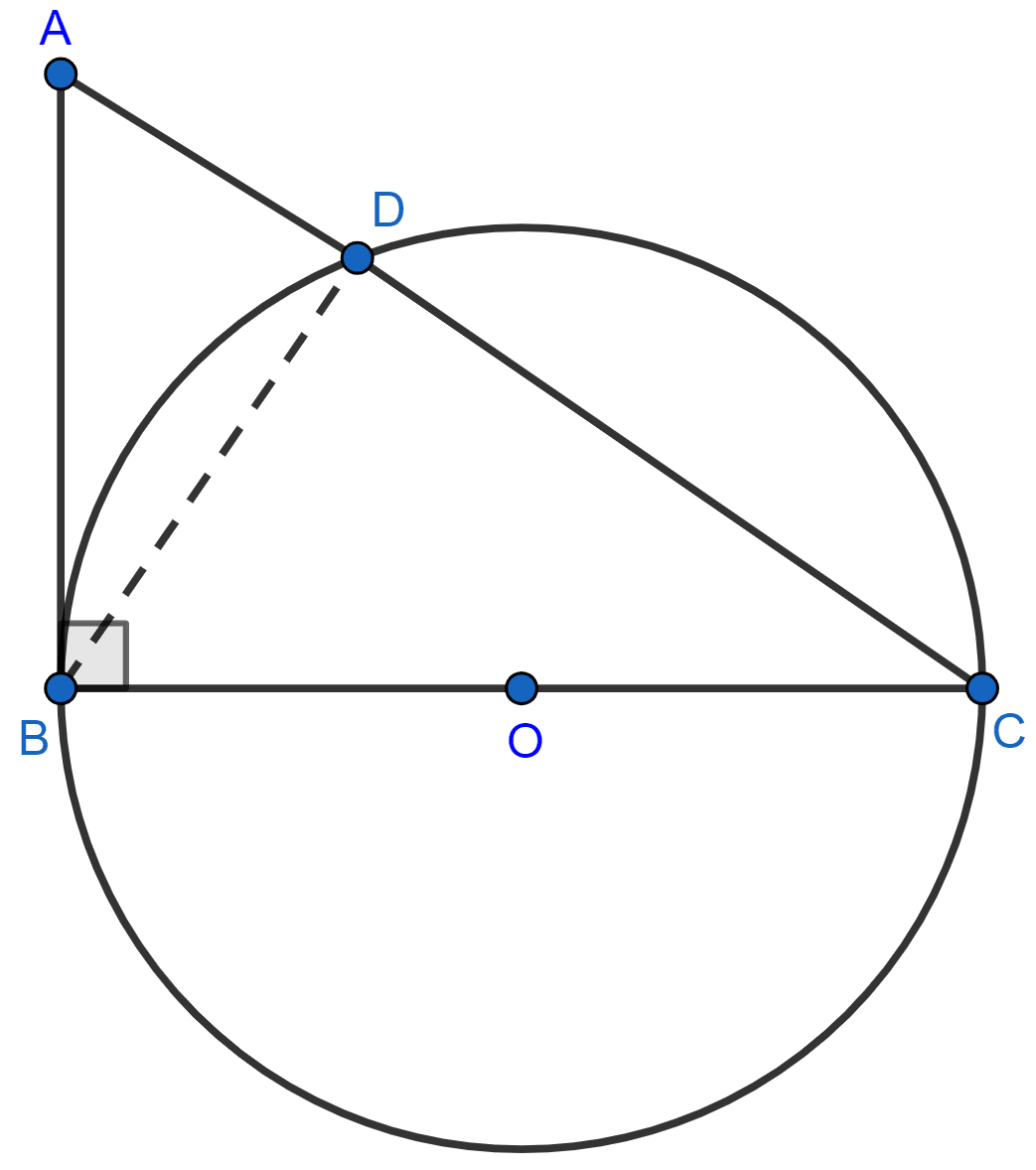
ABC is a right triangle with angle B = 90°. A circle with BC as diameter meets hypotenuse AC at point D. Prove that:
(i) AC x AD = AB2
(ii) BD2 = AD x DC.
Circles
4 Likes
Answer
(i) In ∆ABC, we have
∠B = 90° and BC is the diameter of the circle.
Hence, AB is the tangent to the circle at B.
We know that,
If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ AB2 = AD x AC.
Hence, proved that AB2 = AD x AC.
(ii) From figure,
∠BDC = 90° [Angle in a semi-circle is a right angle.]
From figure,
⇒ ∠ADB + ∠BDC = 180° [Linear pairs]
⇒ ∠ADB + 90° = 180°
⇒ ∠ADB = 180° - 90°
⇒ ∠ADB = 90°
In ∆ADB,
⇒ ∠ADB + ∠A + ∠ABD = 180° [By angle sum property of triangle]
⇒ 90° + ∠A + ∠ABD = 180°
⇒ ∠A + ∠ABD = 90° ……………(1)
In ∆ABC, ∠ABC = 90°.
⇒ ∠ABC + ∠A + ∠ACB = 180° [By angle sum property of triangle]
⇒ 90° + ∠A + ∠ACB = 180°
⇒ ∠A + ∠ACB = 90° ……………(2)
From (1) and (2),
⇒ ∠A + ∠ABD = ∠A + ∠ACB
⇒ ∠ABD = ∠ACB.
From figure,
⇒ ∠ACB = ∠BCD
∴ ∠ABD = ∠BCD
Now in ∆ABD and ∆CBD, we have
∠BDA = ∠BDC [Both equal to 90°]
∠ABD = ∠BCD
Hence, ∆ABD ~ ∆CBD by AA postulate.
We know that,
Ratio of corresponding sides of similar triangles are same.
∴ BD2 = AD x DC.
Hence, proved that BD2 = AD x DC.
Answered By
2 Likes
Related Questions
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If ∠DCQ = 40° and ∠ABD = 60°, find:
(i) ∠DBC
(ii) ∠BCP
(iii) ∠ADB

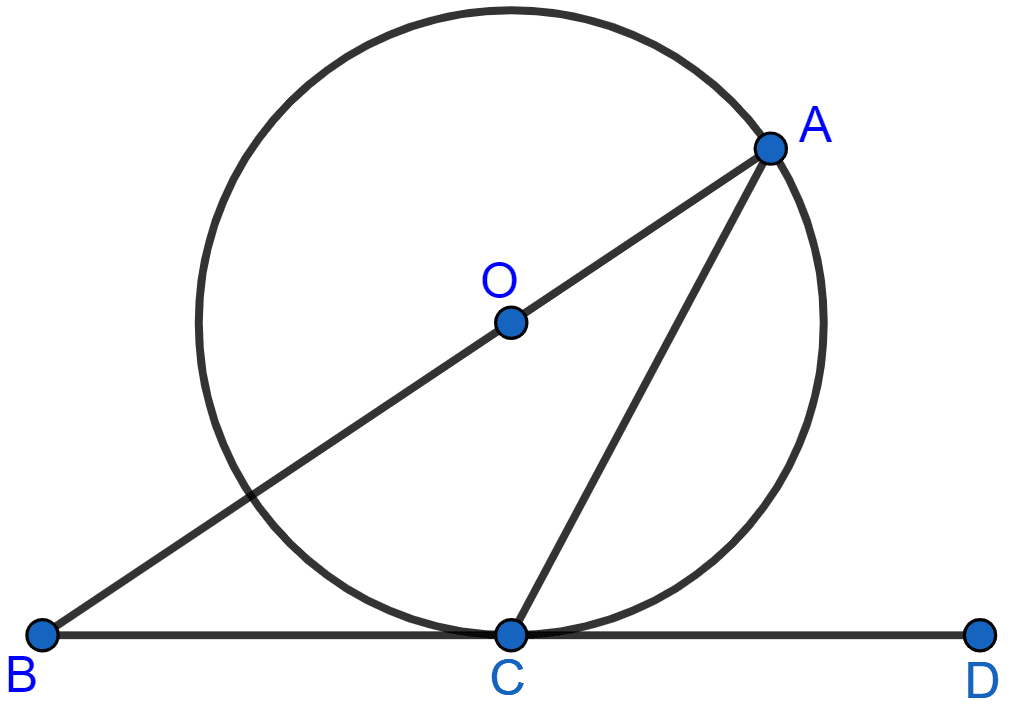
The given figure shows a circle with centre O and BCD is a tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.
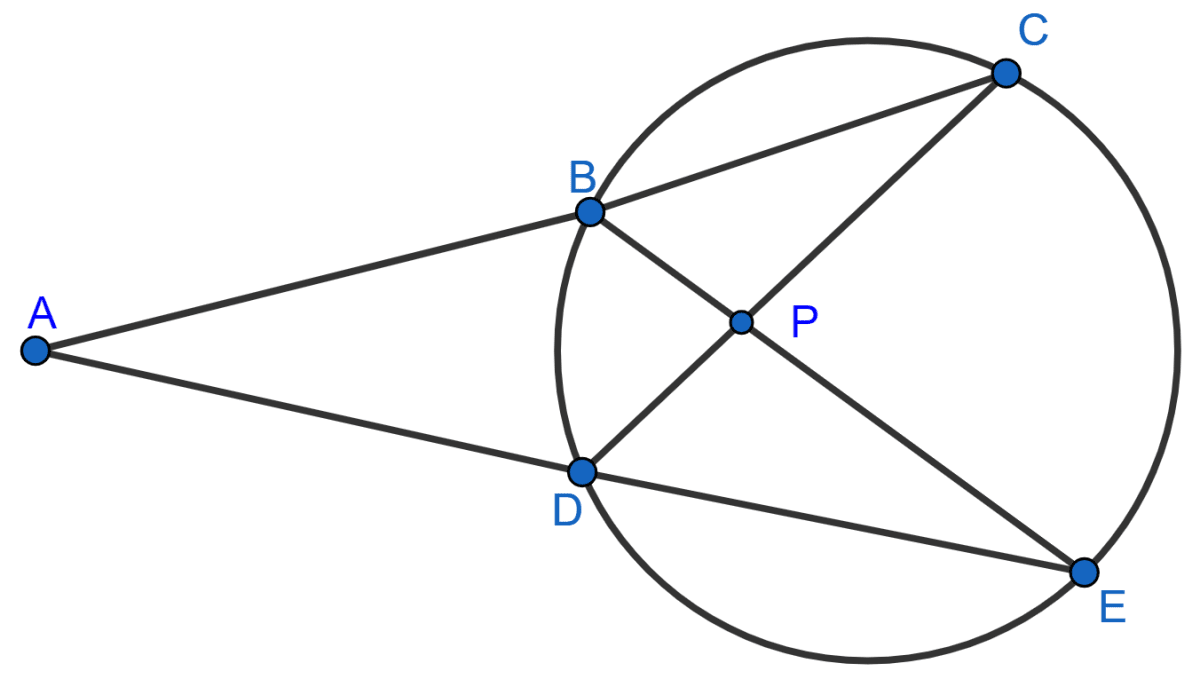
In the given figure, AC = AE.
Show that :
(i) CP = EP
(ii) BP = DP
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate :
(i) ∠BEC
(ii) ∠BED