Mathematics
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate :
(i) ∠BEC
(ii) ∠BED
Circles
2 Likes
Answer
Cyclic pentagon ABCDE with its circumcircle with centre at point O is shown in the figure below:
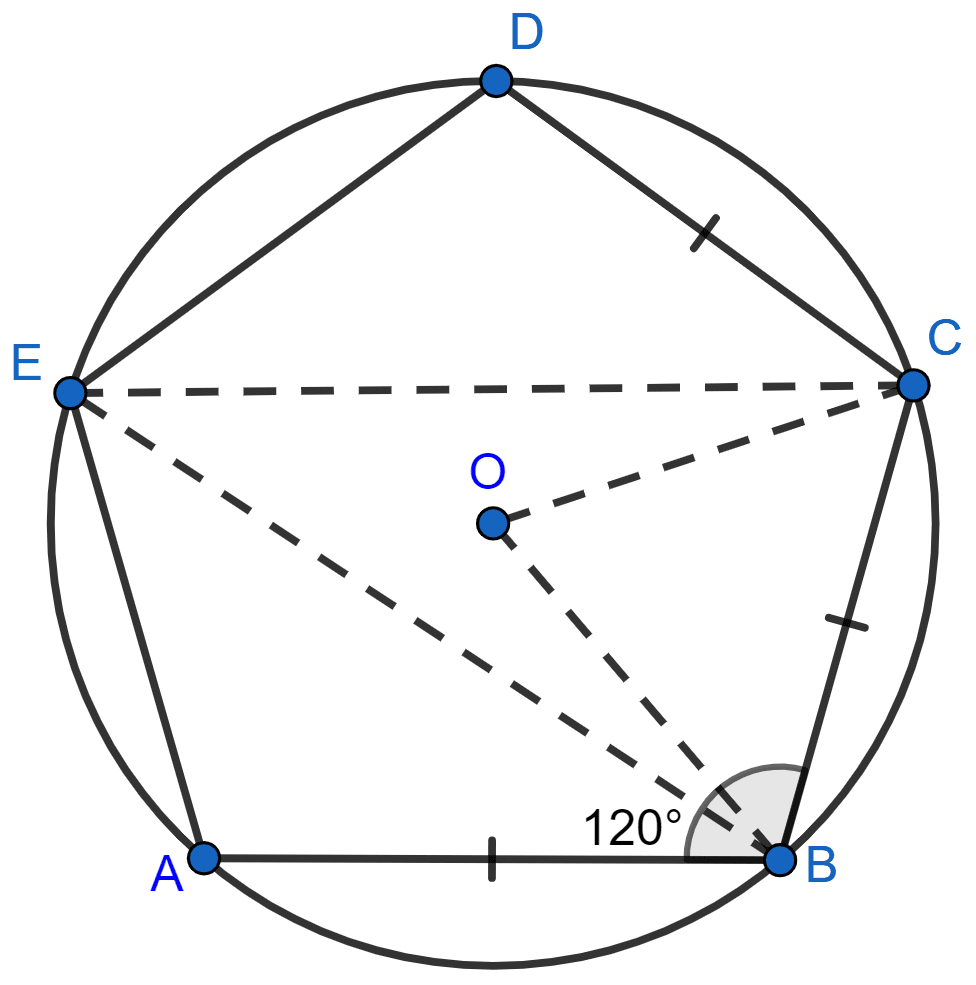
(i) Given,
AB = BC = CD and ∠ABC = 120°
So, ∠BCD = ∠ABC = 120°
OB and OC are the bisectors of ∠ABC and ∠BCD, respectively.
So, ∠OBC = ∠BCO = 60°
In ∆BOC,
⇒ ∠OBC + ∠BCO + ∠BOC = 180° [By angle sum property of triangle]
⇒ 60° + 60° + ∠BOC = 180°
⇒ ∠BOC = 180° - 120° = 60°.
Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
We know that.
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∠BEC = ∠BOC = x 60° = 30°.
Hence, ∠BEC = 30°.
(ii) In cyclic quadrilateral BCDE, we have
⇒ ∠BED + ∠BCD = 180° [Sum of opposite angles in cyclic quadrilateral = 180°]
⇒ ∠BED + 120° = 180°
⇒ ∠BED = 180° - 120°
⇒ ∠BED = 60°.
Hence, ∠BED = 60°.
Answered By
2 Likes
Related Questions
ABC is a right triangle with angle B = 90°. A circle with BC as diameter meets hypotenuse AC at point D. Prove that:
(i) AC x AD = AB2
(ii) BD2 = AD x DC.
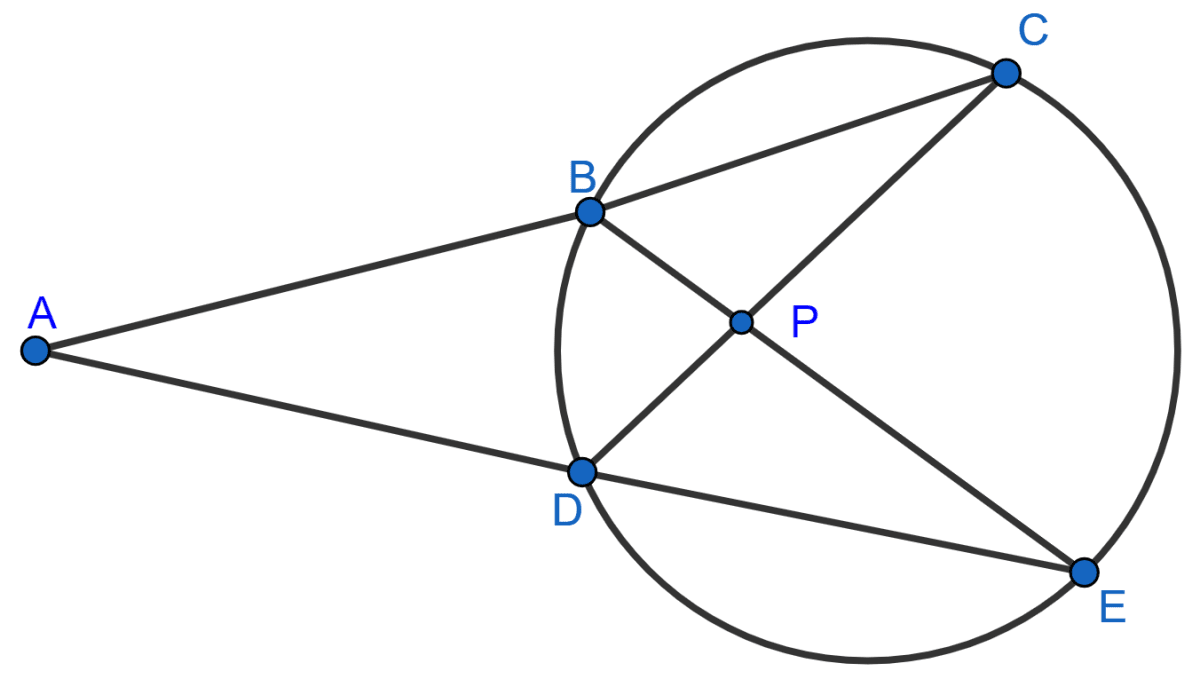
In the given figure, AC = AE.
Show that :
(i) CP = EP
(ii) BP = DP
In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB

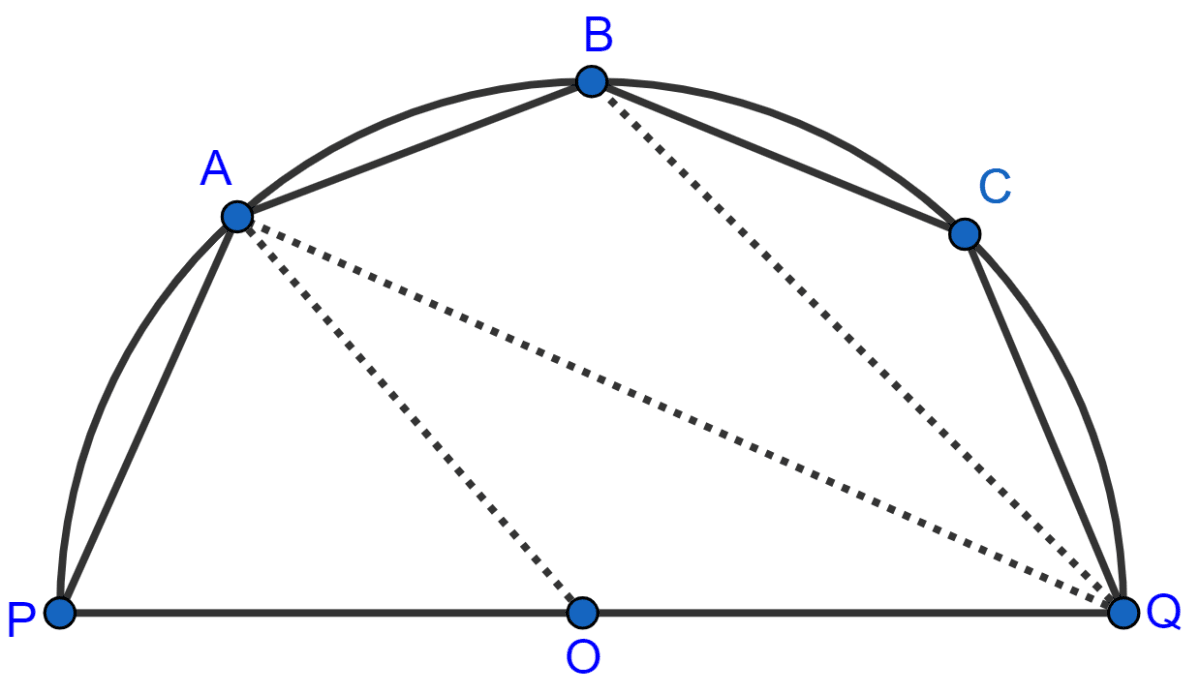
The given figure shows a semi-circle with center O and diameter PQ. If PA = AB and ∠BCQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.