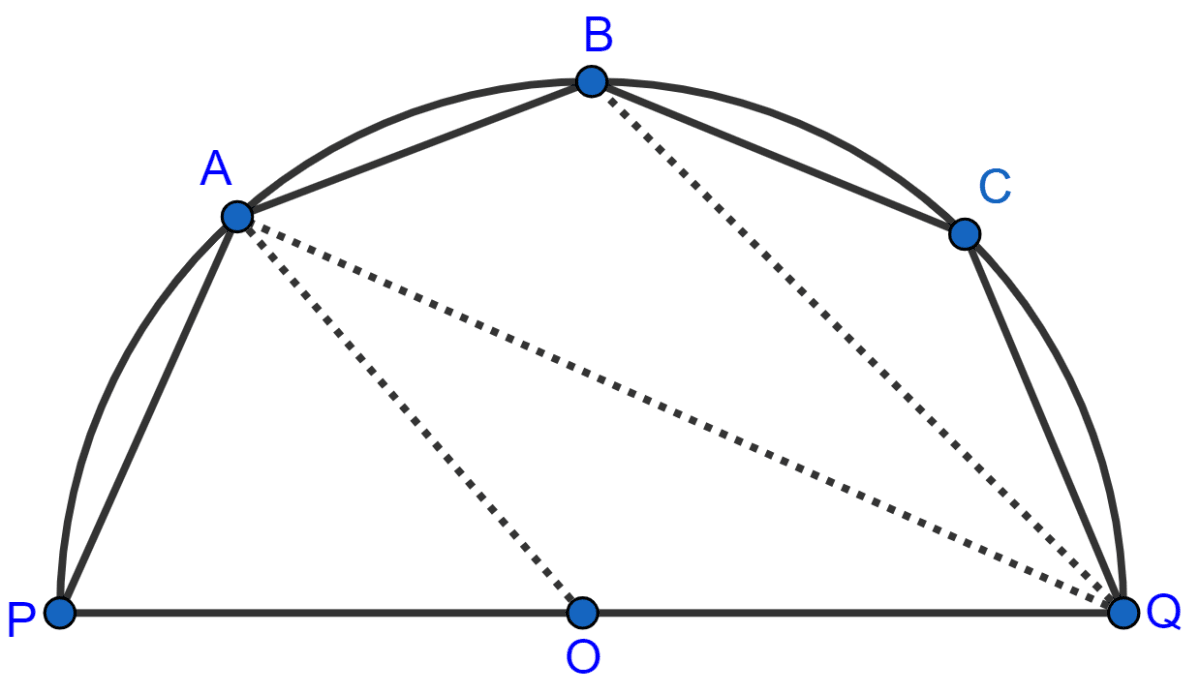
The given figure shows a semi-circle with center O and diameter PQ. If PA = AB and ∠BCQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.

Join PB.

In cyclic quadrilateral PBCQ,

⇒ ∠BPQ + ∠BCQ = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ ∠BPQ + 140° = 180°

⇒ ∠BPQ = 180° - 140°

⇒ ∠BPQ = 40° …………(1)

In △PBQ,

∠PBQ = 90° [Angle in a semi-circle is a right angle.]

⇒ ∠PBQ + ∠BPQ + ∠PQB = 180° [Angle sum property of triangle]

⇒ 90° + 40° + ∠PQB = 180°

⇒ 130° + ∠PQB = 180°

⇒ ∠PQB = 180° - 130°

⇒ ∠PQB = 50°.

In cyclic quadrilateral PQBA,

⇒ ∠PQB + ∠PAB = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ 50° + ∠PAB = 180°

⇒ ∠PAB = 180° - 50°

⇒ ∠PAB = 130°.

In △PAB,

⇒ ∠PAB + ∠PBA + ∠BPA = 180° [Angle sum property of triangle]

⇒ 130° + ∠PBA + ∠BPA = 180°

⇒ ∠PBA + ∠BPA = 180° - 130°

⇒ ∠PBA + ∠BPA = 50° …………….(2)

Given, PA = PB

Angles opposite to equal sides are equal.

∴ ∠PBA = ∠BPA = x (let)

Substituting above value in (2), we get :

⇒ x + x = 50°

⇒ 2x = 50°

⇒ x = $\dfrac{50°}{2}$

⇒ x = 25°.

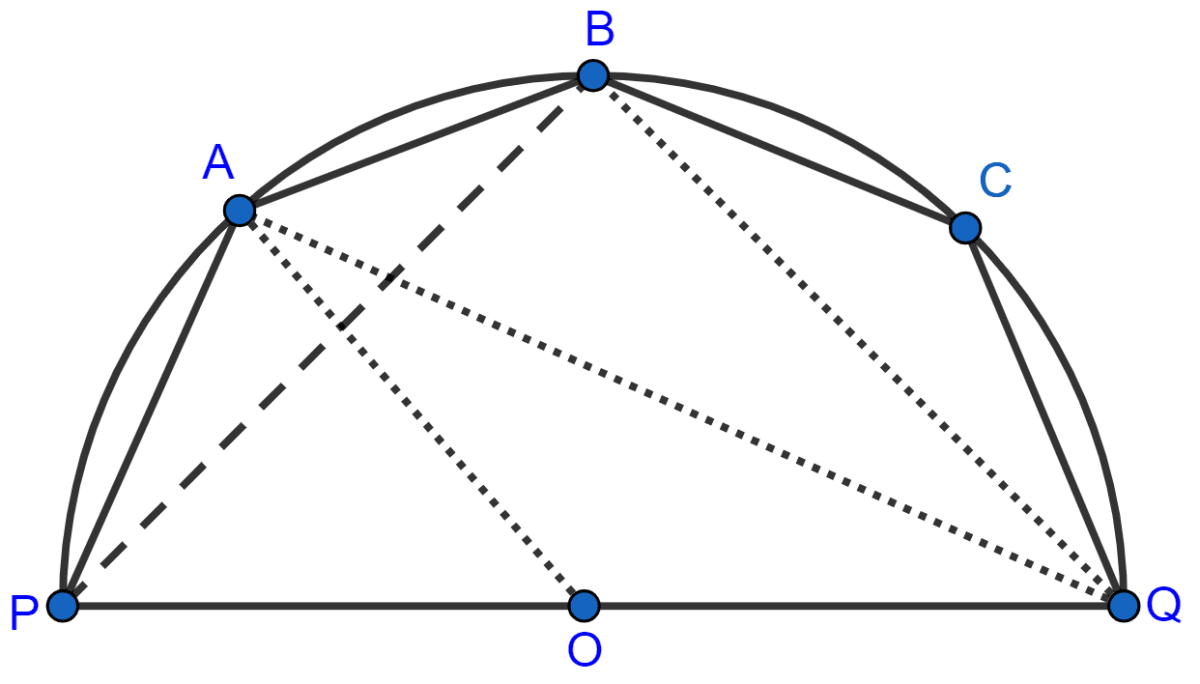
From figure,

∠AQB = ∠APB = 25° [Angles in same segment are equal.]

∠APQ = ∠APB + ∠BPQ = 25° + 40° = 65.

We know that,

Angle subtended by an arc at the center is twice the angle subtended at any other point of circumference.

Arc AQ subtends ∠AOQ at the center and ∠APQ at the remaining part of the circle.

∠AOQ = 2∠APQ = 2 × 65° = 130°.

In △AOQ,

OA = OQ [Radii of same circle]

As, angles opposite to equal sides are equal.

∠OAQ = ∠OQA = y (let)

⇒ ∠OAQ + ∠OQA + ∠AOQ = 180° [Angle sum property of triangle]

⇒ y + y + 130° = 180°

⇒ 2y = 180° - 130°

⇒ 2y = 50°

⇒ y = $\dfrac{50°}{2}$

⇒ y = 25°.

∴ ∠OAQ = 25°.

Since, ∠OAQ = ∠AQB = 25°.

∠OAQ and ∠AQB are alternate angles.

Thus, AO and BQ are parallel.

Hence, ∠AQB = 25° and ∠PAB = 130°.