Mathematics
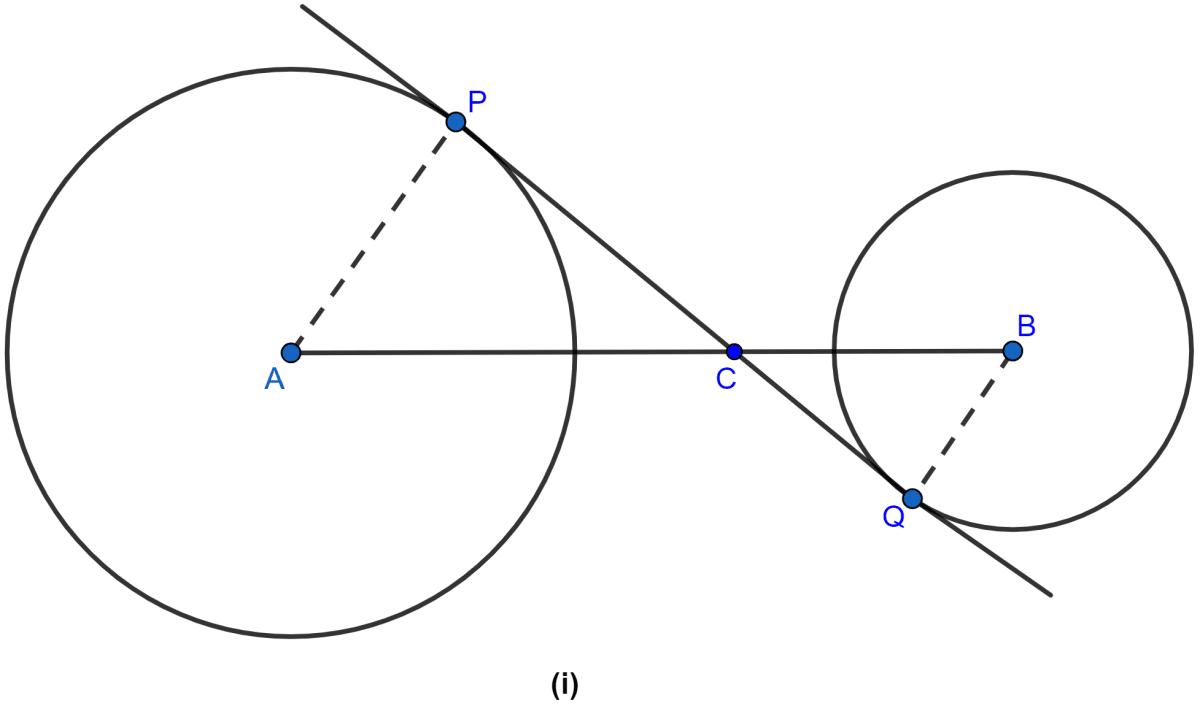
The figure given below shows two circles with centres A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that :
AP : BQ = PC : CQ.
Circles
4 Likes
Answer
In △APC and △BQC
∠PCA = ∠QCB (∵ vertically opposite angles are equal)
∠APC = ∠BQC (∵ both are equal to 90 as radius and tangent to a circle at the point of contact are perpendicular to each other.)
∴ △APC ~ △BQC (By AA axiom of similarity)
Since triangles are similar hence the ratio of their corresponding sides are equal.
Hence, proved that AP : BQ = PC : CQ
Answered By
2 Likes
Related Questions
Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.
From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of the chord AB.
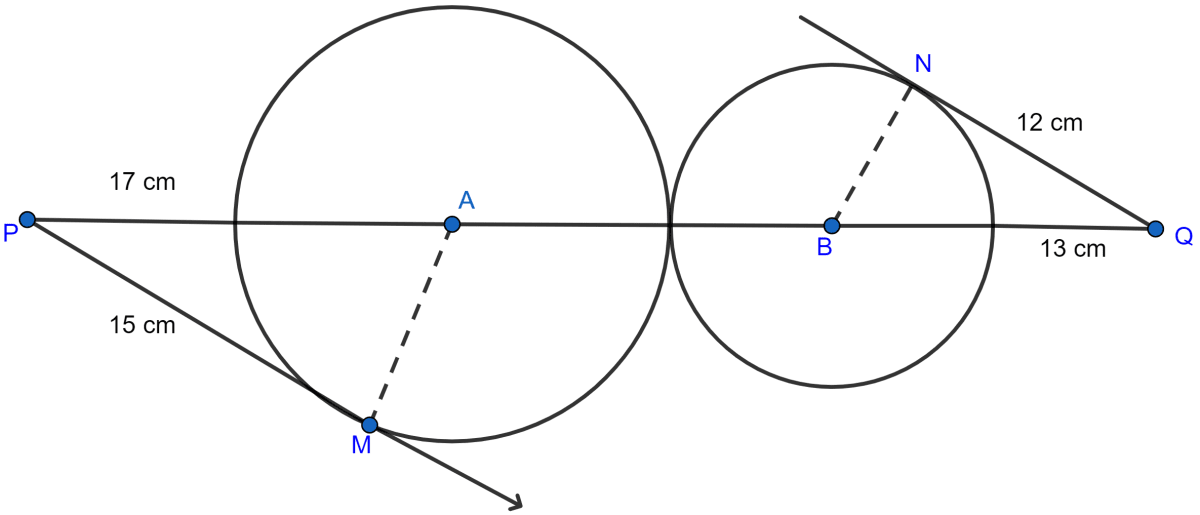
In the figure given below, two circles with centres A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centres A and B of the circles.
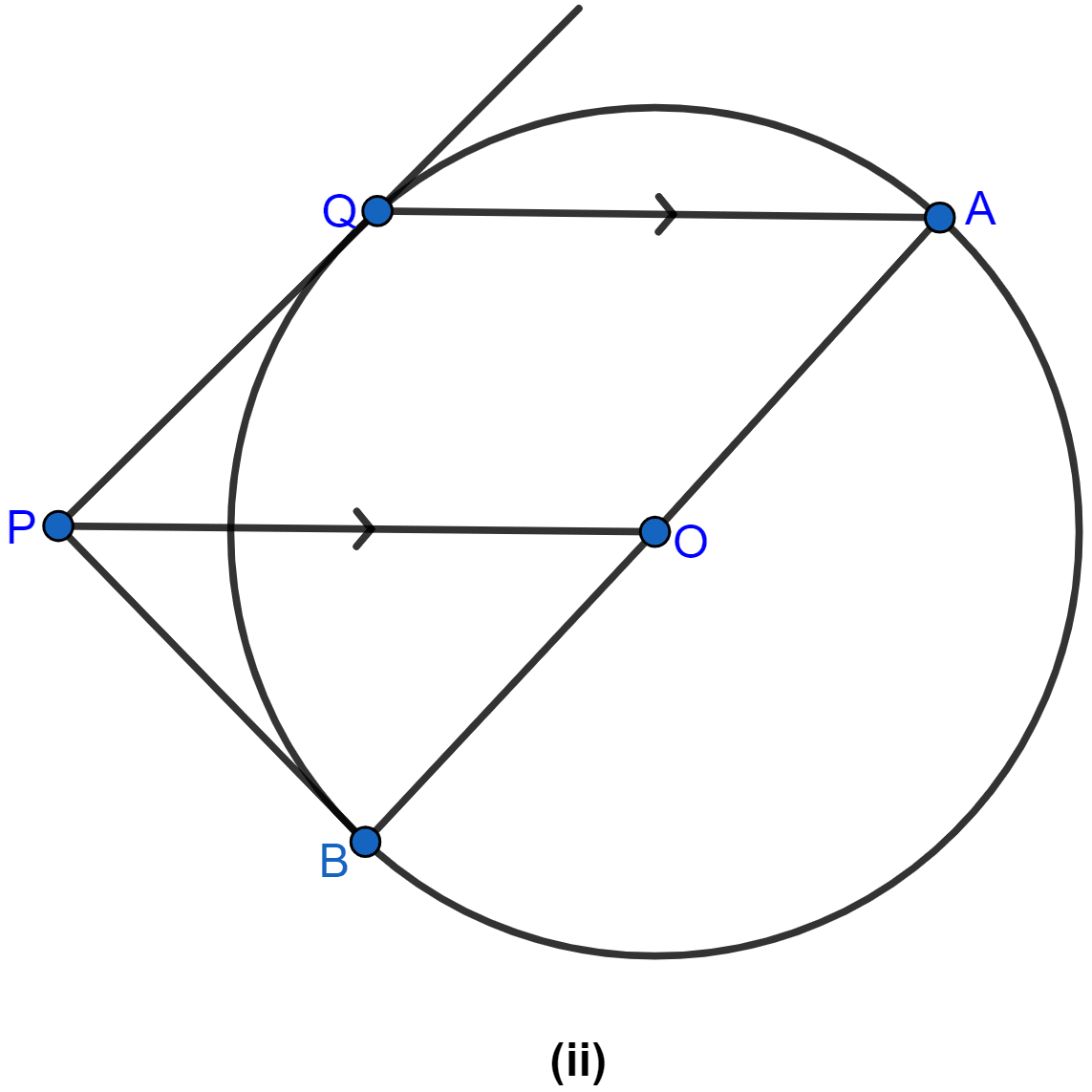
In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.