Mathematics
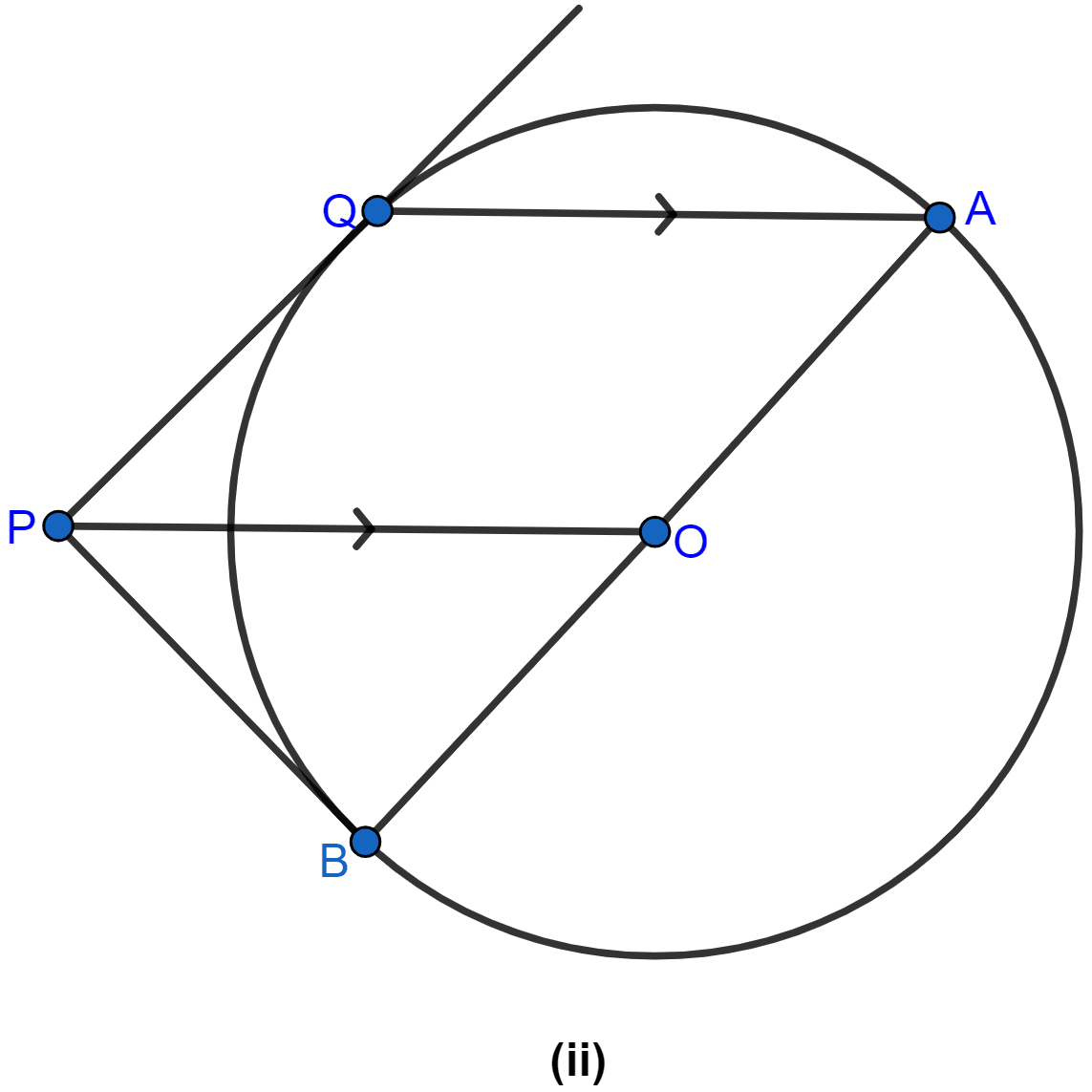
In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
Circles
19 Likes
Answer
Join OQ as shown in the figure below:
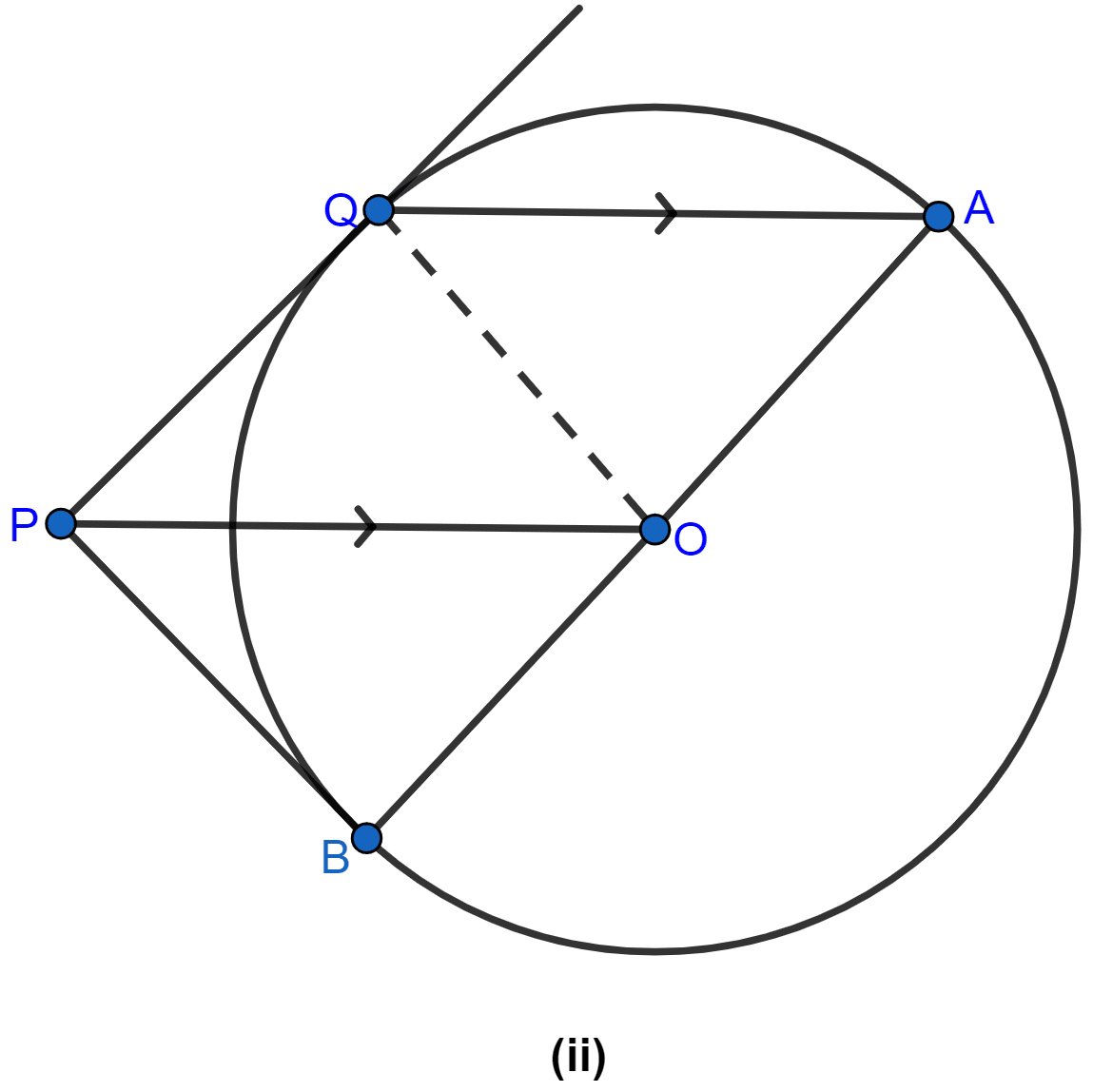
In △OAQ,
OA = OQ (Radius of the same circle.)
∠OAQ = ∠OQA.
Given QA || PO
∴ ∠OAQ = ∠POB (∵ corresponding angles are equal.)
and ∠OQA = ∠QOP (∵ alternate angles are equal.)
But ∠OAQ = ∠OQA,
∴ ∠POB = ∠QOP
Now in △OPQ and △OBP
OP = OP (Common sides)
OQ = OB (Radius of the same circle.)
∠QOP = ∠POB
∴ △OPQ ≅ △OBP (S.A.S. axiom of congruency)
As corresponding parts of congruent triangles are congruent,
∴ ∠OQP = ∠OBP
But ∠OQP = 90°
∴ ∠OBP = 90°
∴ PB is the tangent of the circle.
Hence, proved that PB is the tangent of the circle.
Answered By
15 Likes
Related Questions
From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of the chord AB.
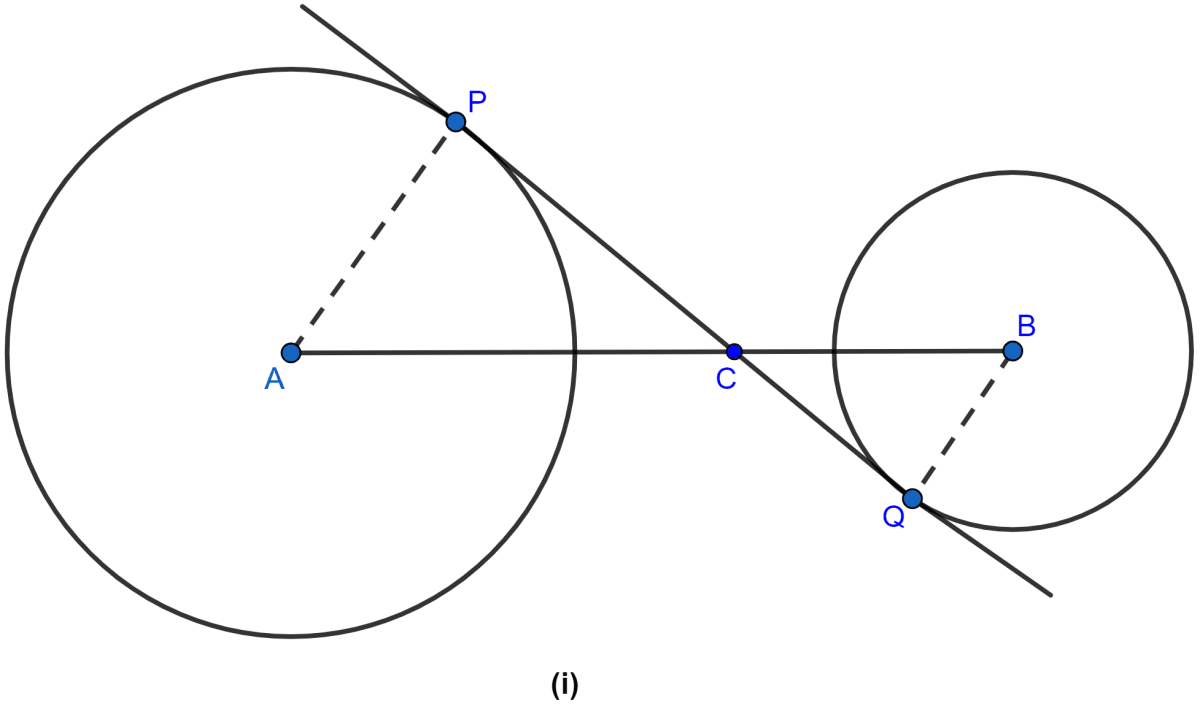
The figure given below shows two circles with centres A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that :
AP : BQ = PC : CQ.
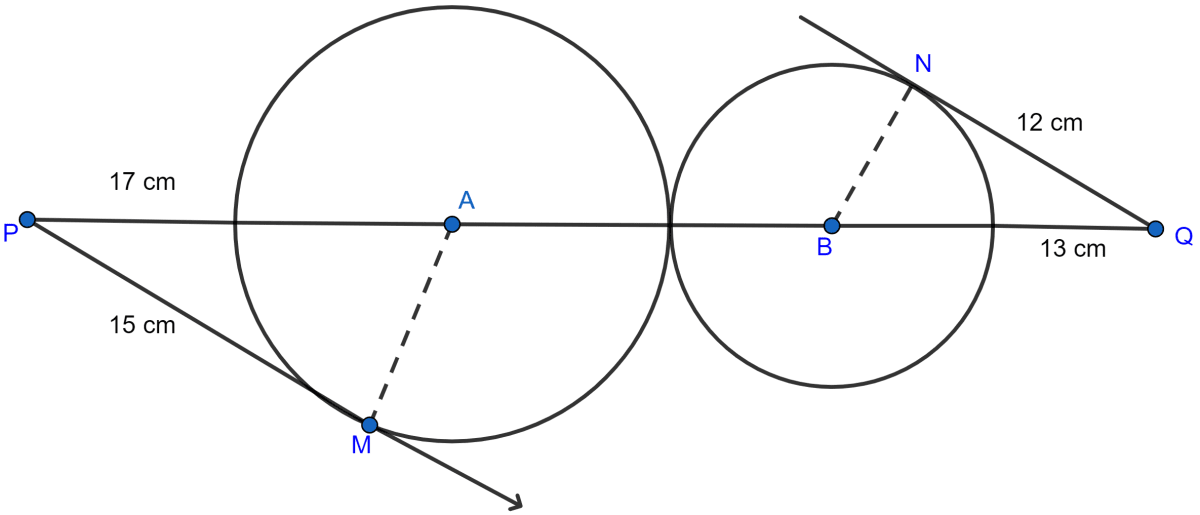
In the figure given below, two circles with centres A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centres A and B of the circles.
Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.