Mathematics
From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of the chord AB.
Circles
2 Likes
Answer
The figure is shown below:
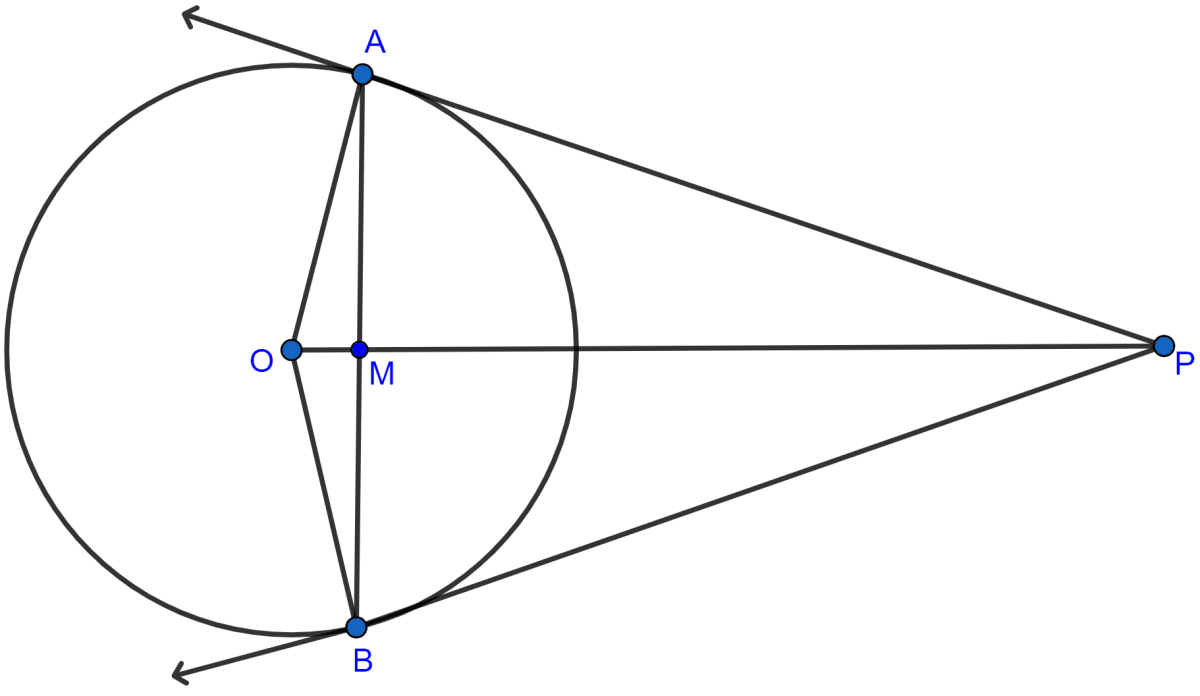
(i) In △AOP and △BOP,
OP = OP (Common sides)
OA = OB (Radius of the circle)
∠OAP = ∠OBP (Both are equal to 90° as tangents and radius on point of contact are perpendicular to each other.)
∴ △OAP ≅ △OBP (S.A.S. axiom of congruency)
(As Corresponding parts of congruent triangles are congruent)
∴ ∠AOP = ∠BOP and ∠APO = ∠BPO.
Hence, proved that ∠AOP = ∠BOP.
(ii) In △APM and △BPM,
PM = PM (Common side)
∠APM = ∠BPM (Proved above)
AP = BP (∵ tangents from an exterior point to a circle are equal in length)
∴ △APM ≅ △BPM (S.A.S. axiom of congruency)
(Congruent parts of congruent triangles are congruent.)
∴ AM = BM and ∠AMP = ∠BMP
But ∠AMP + ∠BMP = 180°
∴ ∠AMP = ∠BMP = 90°.
Hence, proved that OP is perpendicular bisector of AB at M.
Answered By
1 Like
Related Questions
Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.
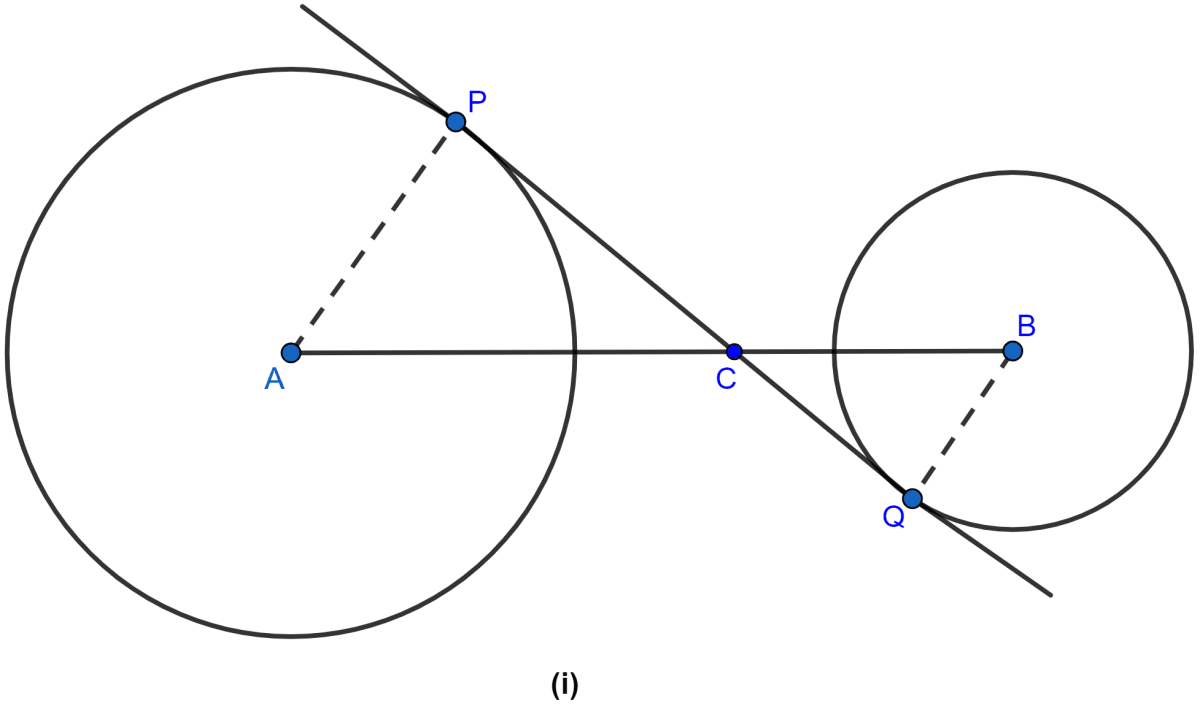
The figure given below shows two circles with centres A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that :
AP : BQ = PC : CQ.
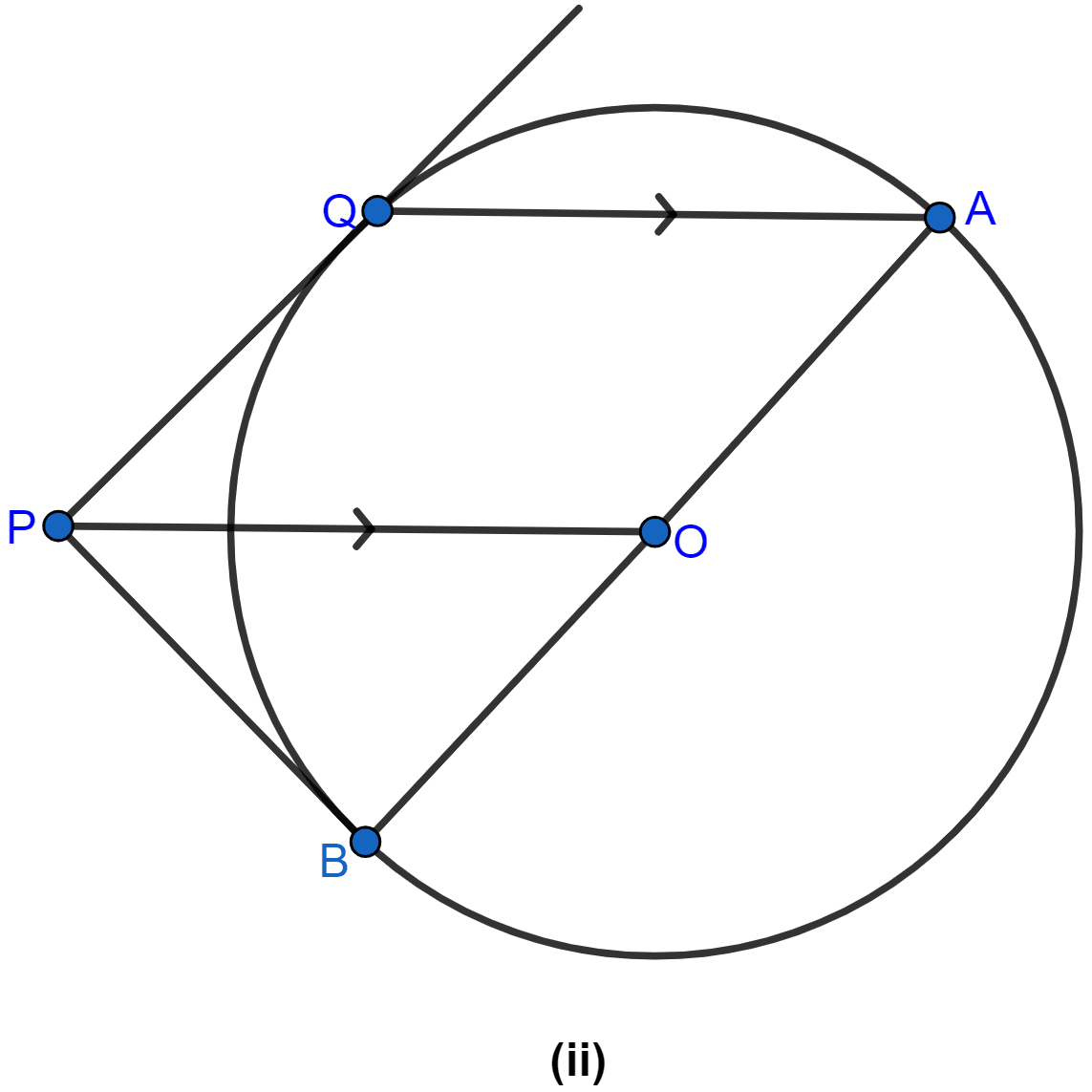
In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
A point P is 13 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 12 cm. Find the distance of P from the nearest point of the circle.