Mathematics
A point P is 13 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 12 cm. Find the distance of P from the nearest point of the circle.
Circles
9 Likes
Answer
Let T be the point of contact of the tangent from point P to the circle with centre O.
From figure,

OT ⊥ PT (As tangent and radius from point of contact are perpendicular to each other.)
In right-angled triangle OPT
⇒ OP2 = OT2 + PT2
⇒ 132 = OT2 + 122
⇒ 169 - 144 = OT2
⇒ OT2 = 25
⇒ OT = 5 cm.
From figure,
⇒ OA = OT = 5 cm (Radius of the circle.)
⇒ PA = OP - OA = 13 - 5 = 8 cm.
Hence, the distance of P from the nearest point of circle = 8 cm.
Answered By
5 Likes
Related Questions
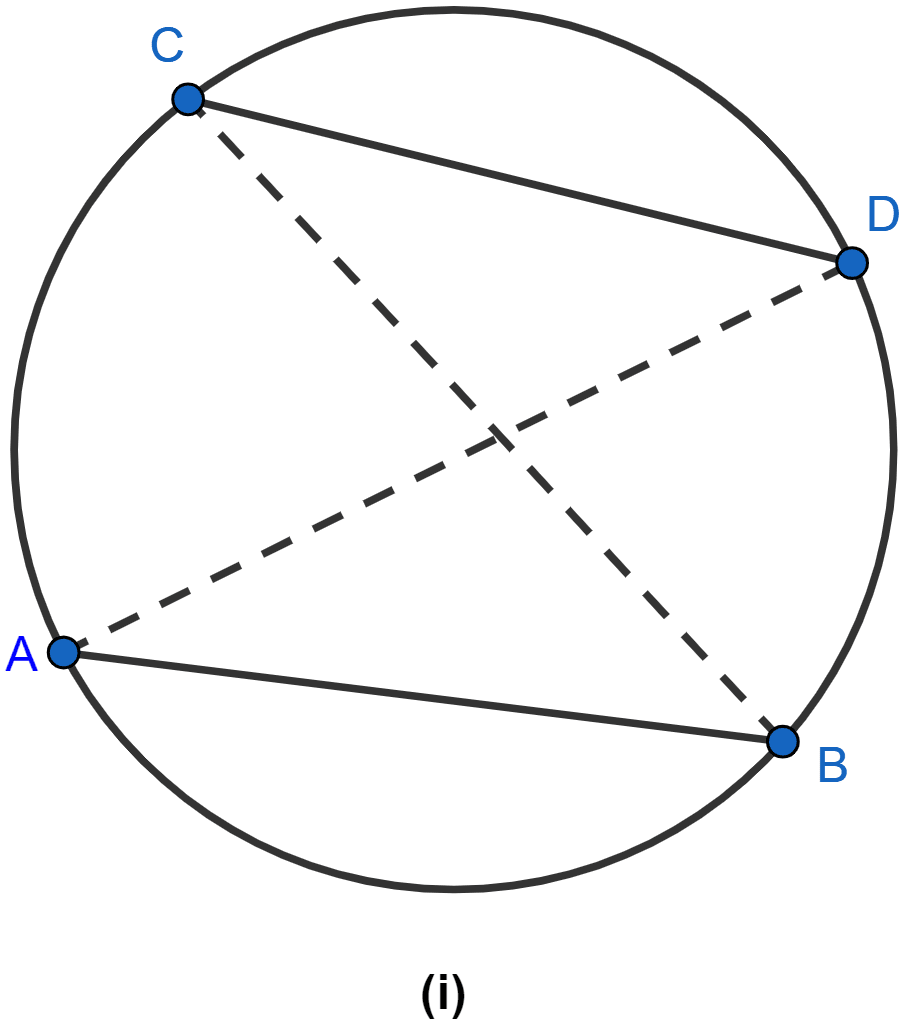
In the figure (i) given below, ABDC is a cyclic quadrilateral. If AB = CD, prove that AD = BC.
In the figure (ii) given below, ABC is an isosceles triangle with AB = AC. If ∠ABC = 50°, find ∠BDC and ∠BEC.

Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.
From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of the chord AB.