Mathematics
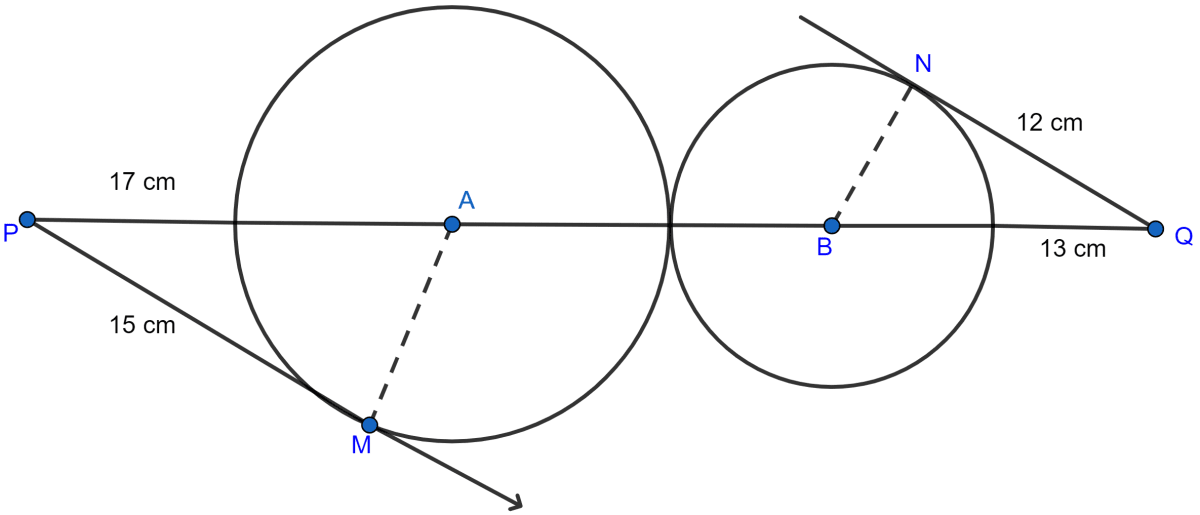
In the figure given below, two circles with centres A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centres A and B of the circles.
Circles
15 Likes
Answer
Since radius and tangent at the point of contact of a circle are perpendicular to each other.
∴ ∠AMP = ∠BNQ = 90°.
In right angled triangle △AMP
AP2 = AM2 + PM2 (By pythagoras theorem)
⇒ AM2 = AP2 - PM2
⇒ AM2 = 172 - 152
⇒ AM2 = 289 - 225
⇒ AM2 = 64
⇒ AM =
⇒ AM = 8 cm.
Similarly in right angled triangle △BNQ
BQ2 = BN2 + NQ2 (By pythagoras theorem)
⇒ BN2 = BQ2 - NQ2
⇒ BN2 = 132 - 122
⇒ BN2 = 169 - 144
⇒ BN2 = 25
⇒ BN =
⇒ BN = 5 cm.
From figure the distance between A and B is equal to the sum of their radius = 8 + 5 = 13 cm.
Answered By
9 Likes
Related Questions
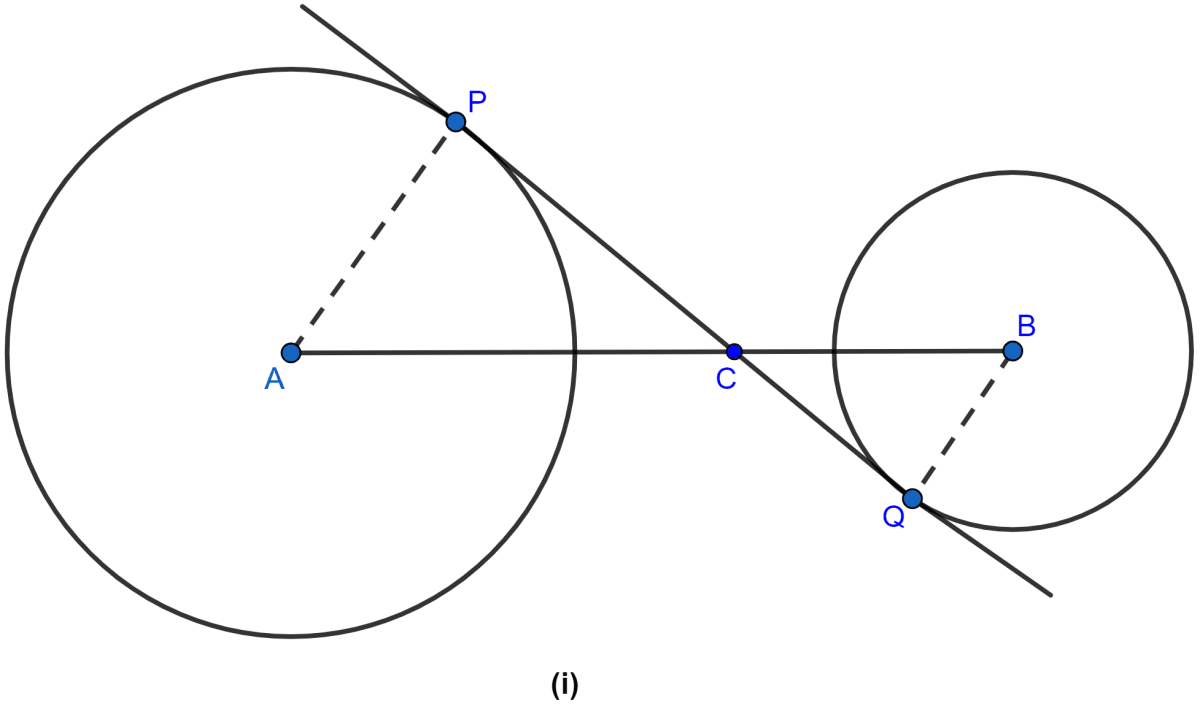
The figure given below shows two circles with centres A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that :
AP : BQ = PC : CQ.
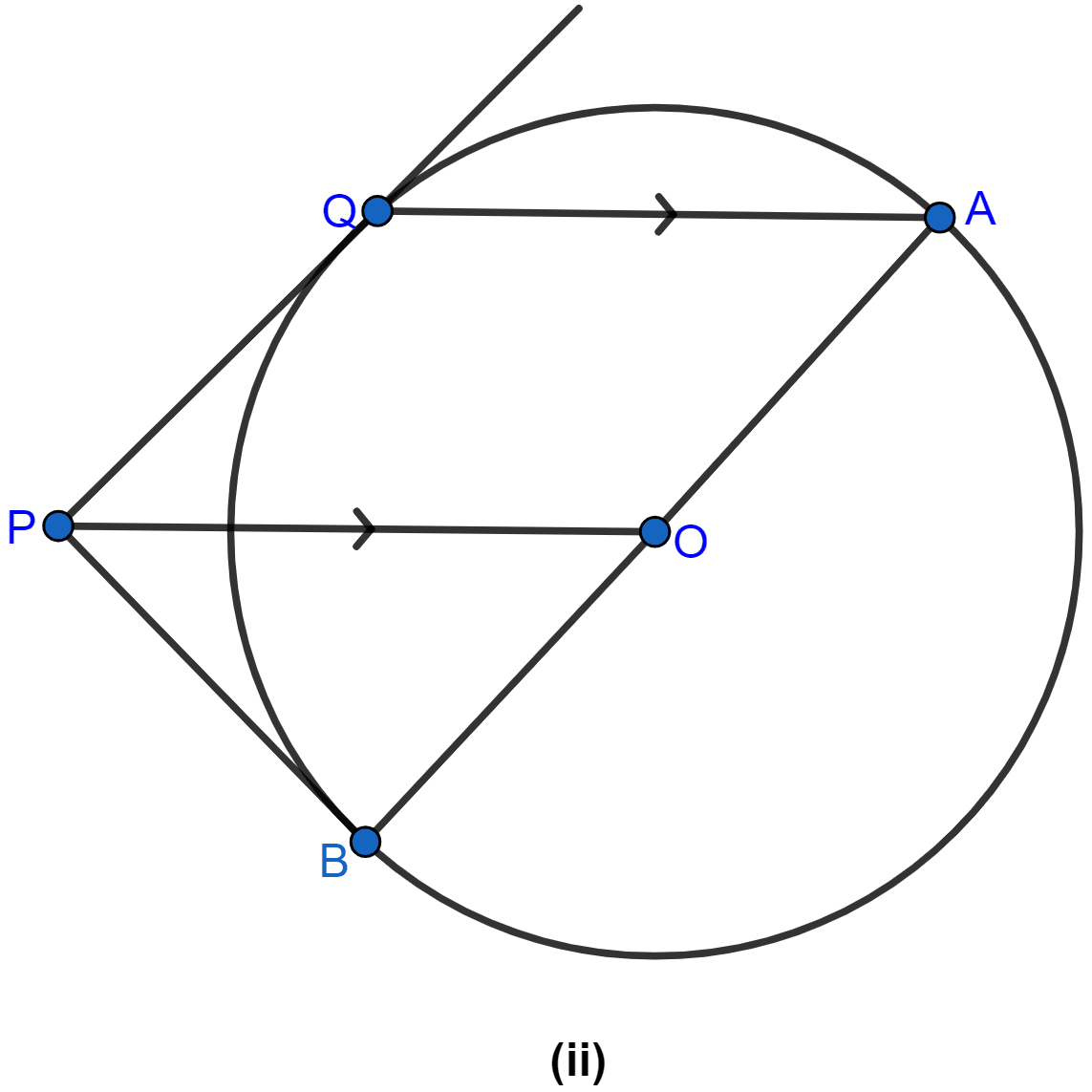
In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.
In the figure (i) given below, chord AB and diameter CD of a circle with centre O meet at P. PT is tangent to the circle at T. If AP = 16 cm, AB = 12 cm and DP = 2 cm, find the length of PT and the radius of the circle.
