Mathematics
TA and TB are tangents to a circle with center O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Answer
Given TA and TB are tangent to a circle with centre O from point T.
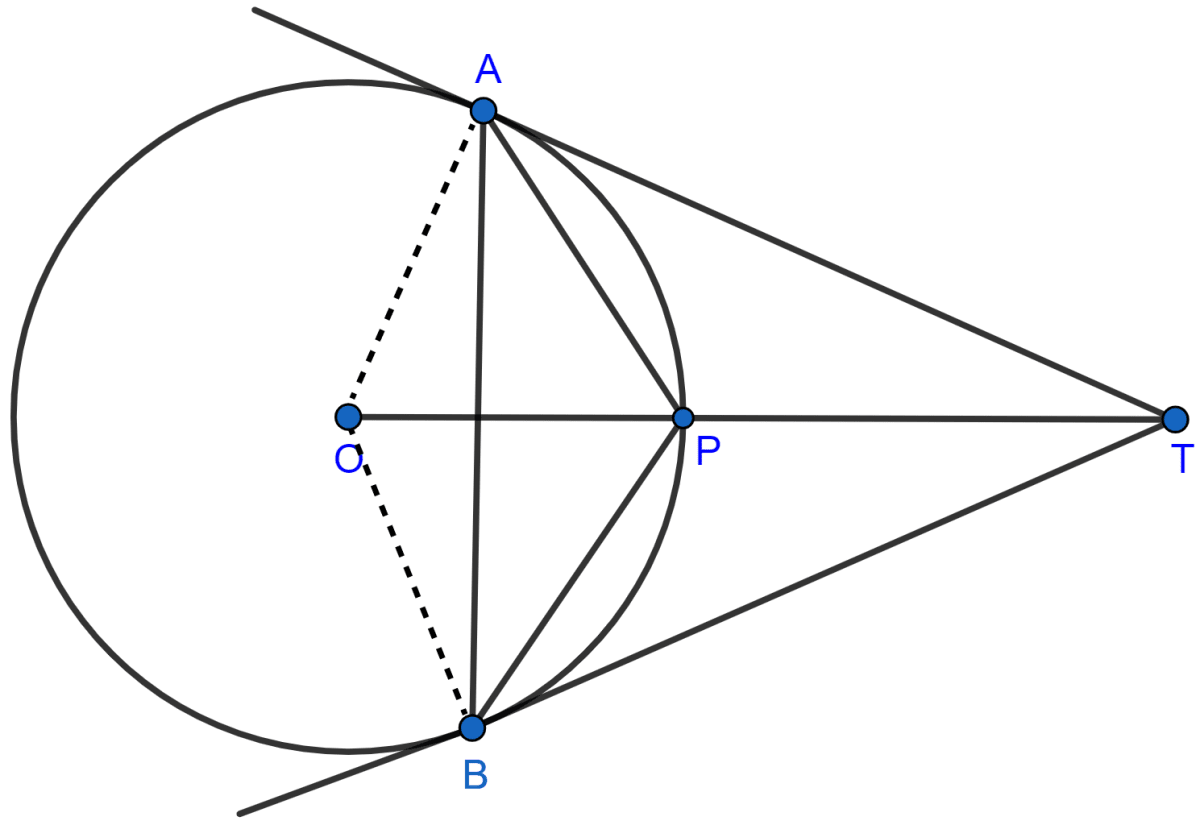
Consider, ΔOAT and ΔOBT
Here, OA = OB [Radii of circle]
OT = OT [Common side]
TA = TB [Tangents from an external point to a circle are equal in length]
∴ ΔOAT ≅ ΔOBT [By SSS congruence criterion]
∴ ∠ATO = ∠BTO [By C.P.C.T.]
⇒ ∠ATP = ∠BTP [From figure, ∠ATO = ∠ATP and ∠BTO = ∠BTP]
In ΔAPT and ΔBPT,
AT = BT [Tangents from an external point to a circle are equal in length]
PT = PT [Common side]
∠ATP = ∠BTP [Proved above]
∴ ΔAPT ≅ ΔBPT [By SAS congruence criterion]
∴ ∠PAT = ∠PBT [By C.P.C.T.]
and AP = BP [By C.P.C.T.]
In ΔPAB,
∠PAB = ∠PBA [Angles opposite to equal sides are equal]
∠PAT = ∠PBA [Angles in alternate segments are equal]
∴ ∠PAB = ∠PAT
∴ AP is the bisector of ∠TAB
Hence, proved that AP bisects ∠TAB.
Related Questions
The given figure shows a circle with center O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate :
(i) angle QTR
(ii) angle QRP
(iii) angle QRS
(iv) angle STR

The given figure shows a semi-circle with center O and diameter PQ. If PA = AB and ∠BCQ = 140°; find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
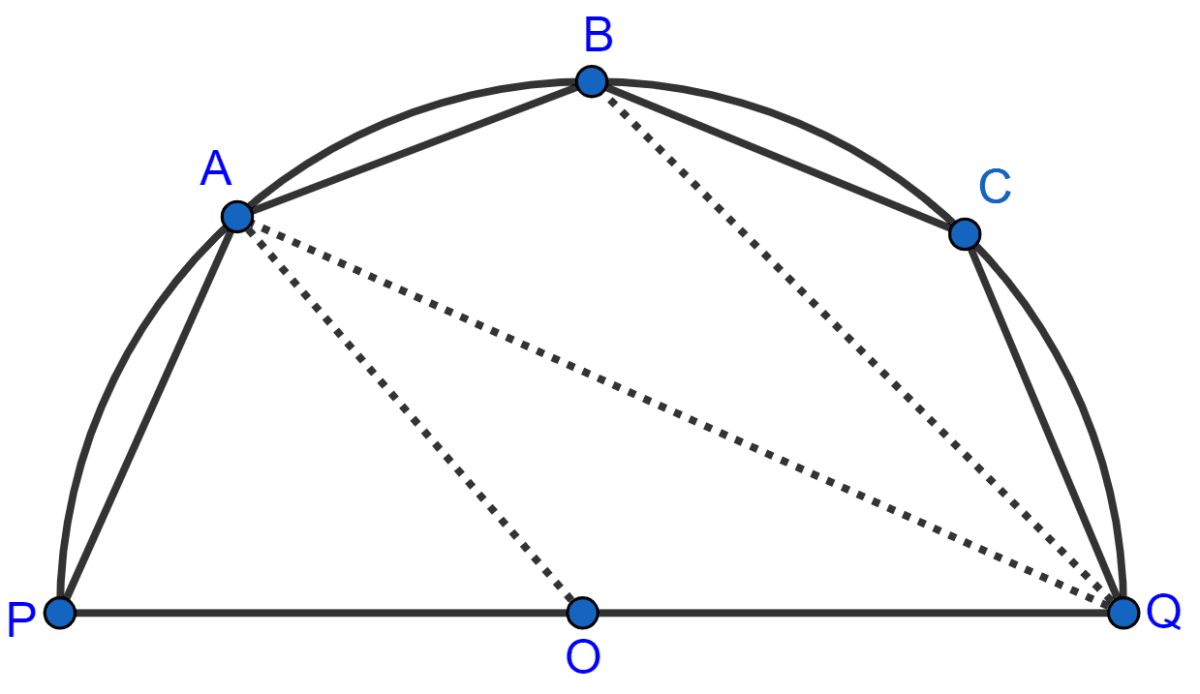
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD.
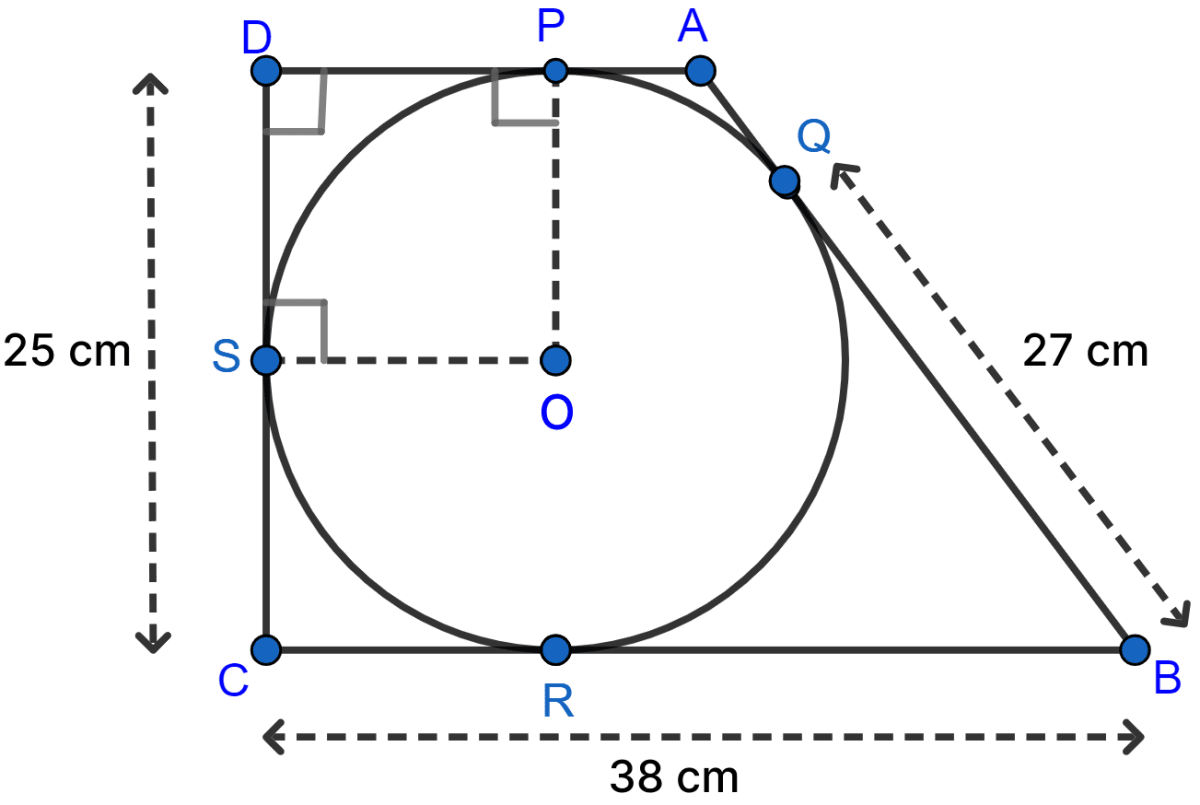
In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.