Mathematics
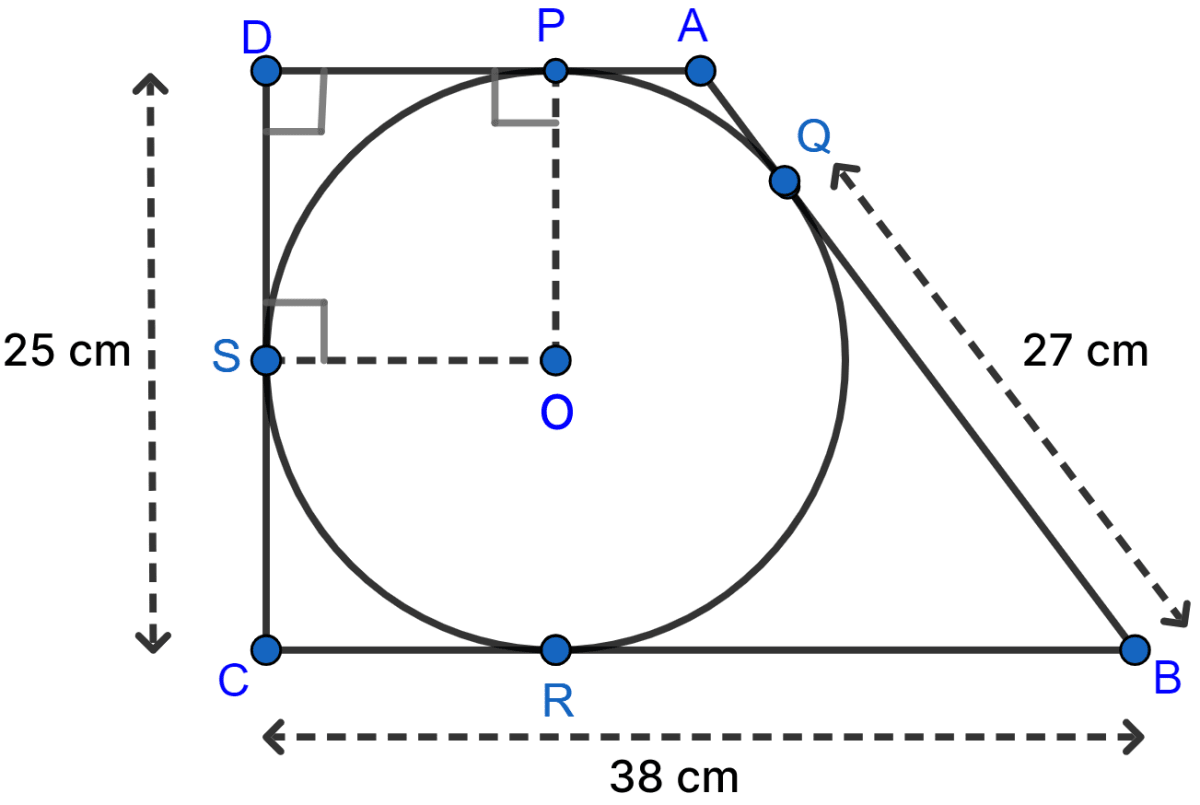
In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
Circles
3 Likes
Answer
From figure,
⇒ BR = BQ = 27 cm [∵ Length of tangents form an external point to a circle are equal.]
⇒ CR = BC - BR = 38 - 27 = 11 cm.
⇒ CR = CS = 11 cm [∵ Length of tangents form an external point to a circle are equal.]
⇒ DS = DC - CS = 25 - 11 = 14 cm.
In quadrilateral DSOP,
⇒ ∠SDP + ∠DPO + ∠OSD + ∠POS = 360°
⇒ 90° + 90° + 90° + ∠POS = 360°
⇒ ∠POS = 360° - 270° = 90°.
Since, all angles are 90° and OS = OP [∵ Both equal to radius of same circle]
Hence, proved that DPOS is a square.
OP = DS = 14 cm.
Hence, radius of circle = 14 cm.
Answered By
1 Like
Related Questions
TA and TB are tangents to a circle with center O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD.
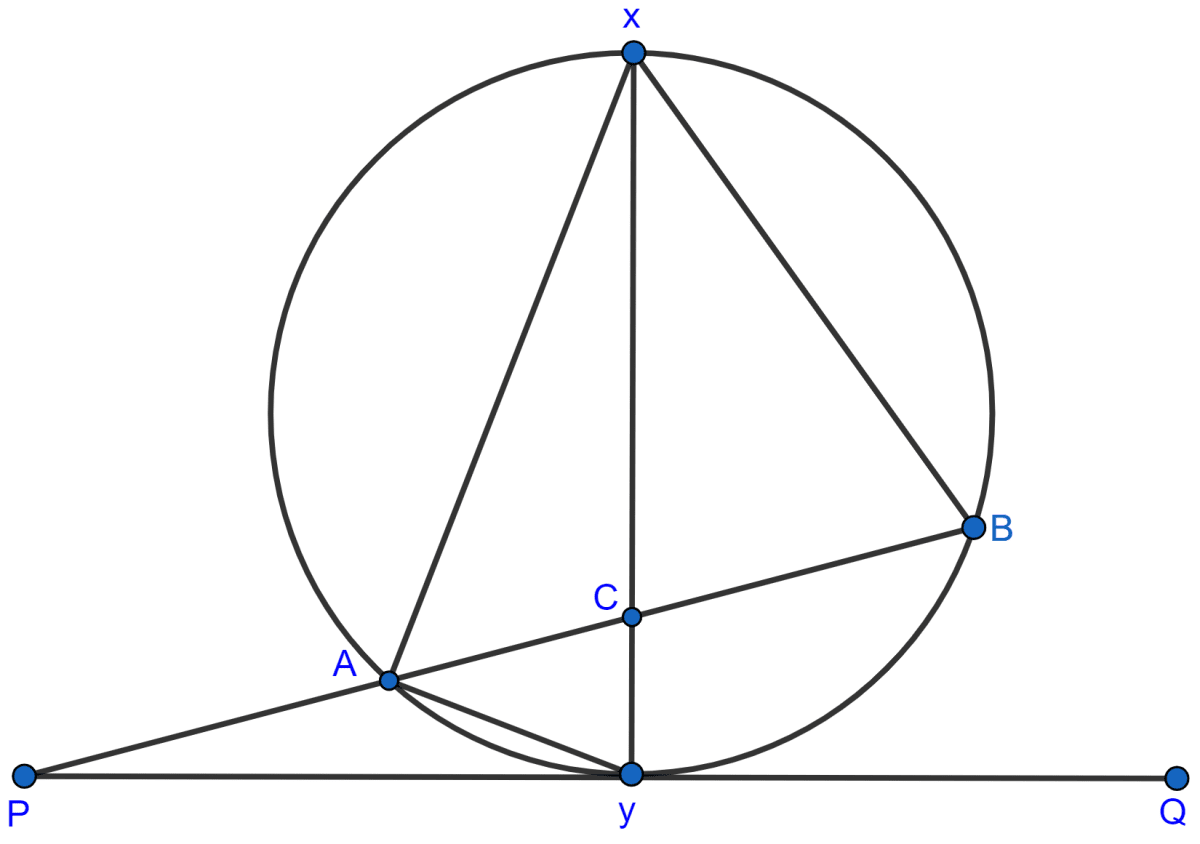
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
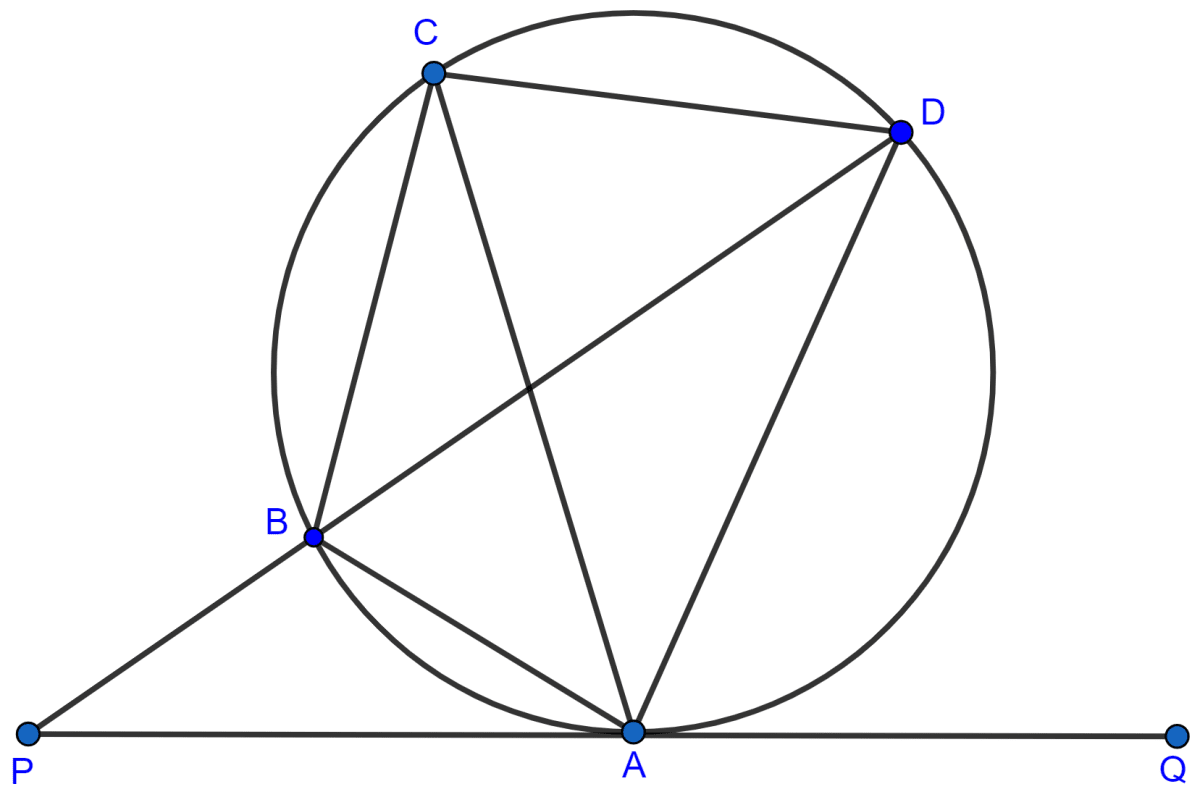
In the given figure, QAP is the tangent at point A and PBD is a straight line.
If ∠ACB = 36° and ∠APB = 42°, find :
(i) ∠BAP
(ii) ∠ABD
(iii) ∠QAD
(iv) ∠BCD