Mathematics
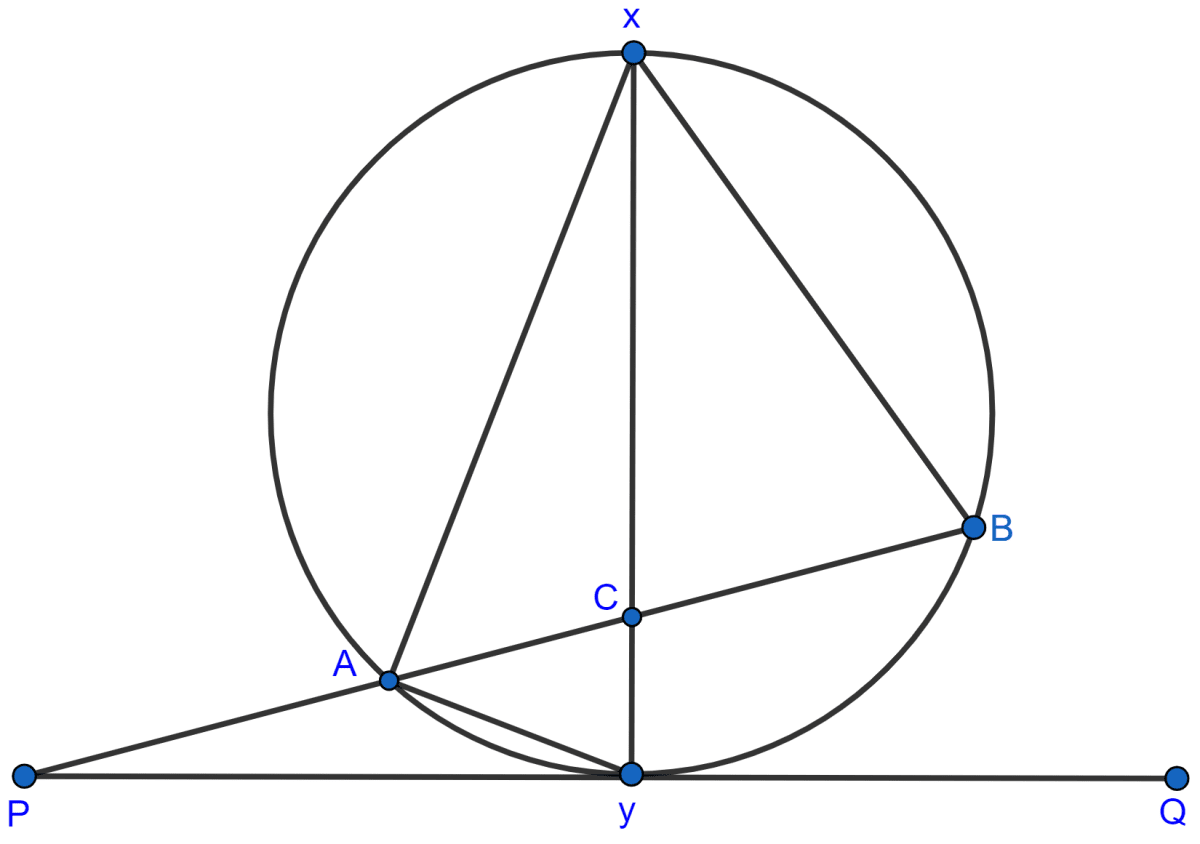
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
Circles
7 Likes
Answer
In △AXB,
⇒ ∠AXB + ∠XAB + ∠ABX = 180° [Angle sum property of triangle]
⇒ 50° + XAB + 70° = 180°
⇒ ∠XAB = 180° - 120° = 60°.
From figure,
∠XAY = 90° [Angle in a semi-circle is a right angle.]
∠BAY = ∠XAY - ∠XAB = 90° - 60 = 30°.
∠BXY = ∠BAY = 30° [Angles in same segment are equal]
We know that,
An exterior angle is equal to the sum of two opposite interior angles.
⇒ ∠ACX = ∠BXC + ∠CBX
⇒ ∠ACX = ∠BXY + ∠ABX [From figure, ∠BXC = ∠BXY and ∠CBX = ∠ABX]
⇒ ∠ACX = 30° + 70° = 100°.
We know that,
Diameter is perpendicular to tangent.
⇒ ∠XYP = 90°
An exterior angle in a triangle is equal to sum of two opposite interior angles.
⇒ ∠ACX = ∠APY + ∠CYP
⇒ ∠APY = ∠ACX - ∠CYP = 100° - 90° = 10°.
Hence, ∠APY = 10° and ∠BAY = 30°.
Answered By
5 Likes
Related Questions
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD.
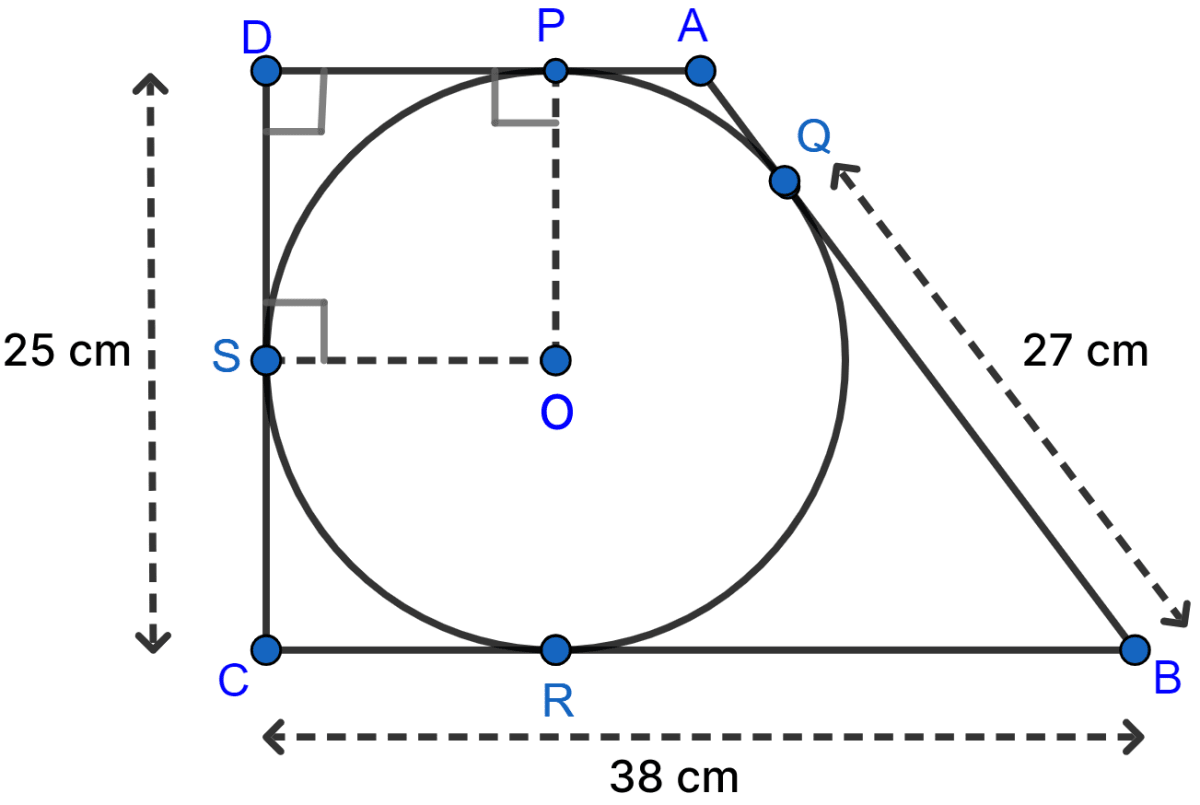
In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
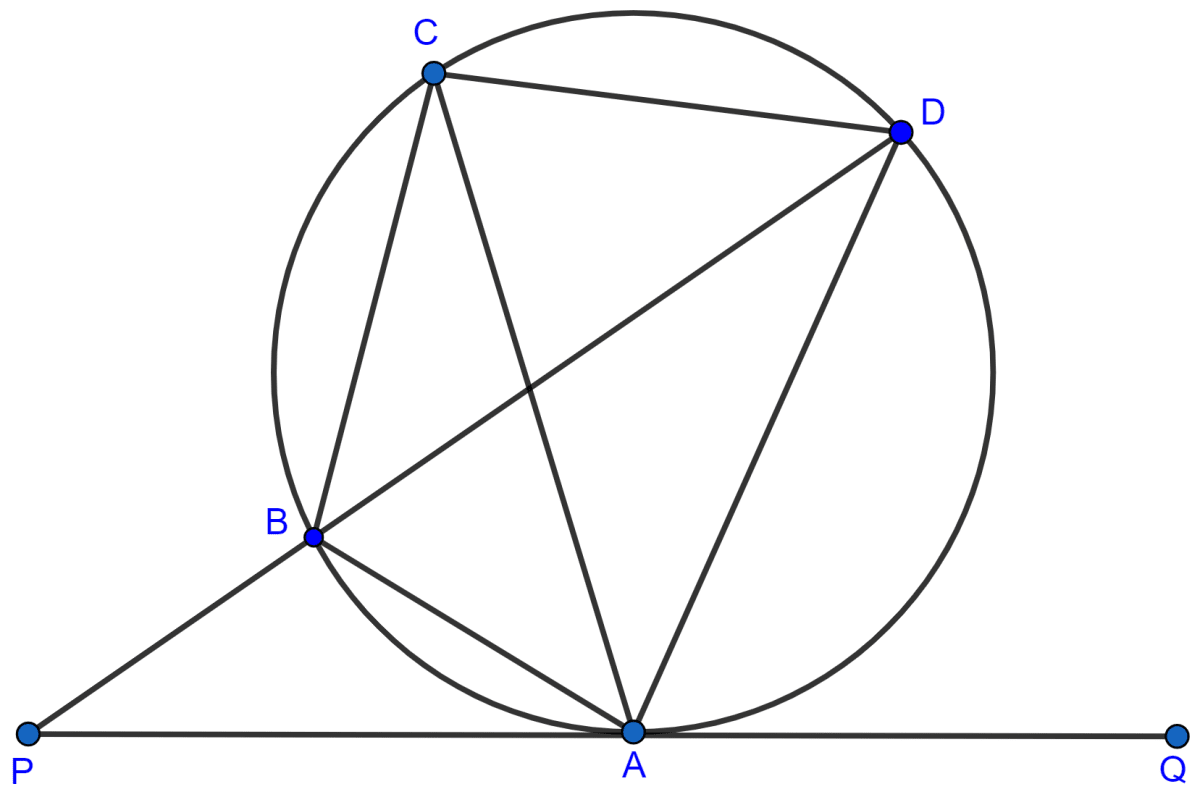
In the given figure, QAP is the tangent at point A and PBD is a straight line.
If ∠ACB = 36° and ∠APB = 42°, find :
(i) ∠BAP
(ii) ∠ABD
(iii) ∠QAD
(iv) ∠BCD
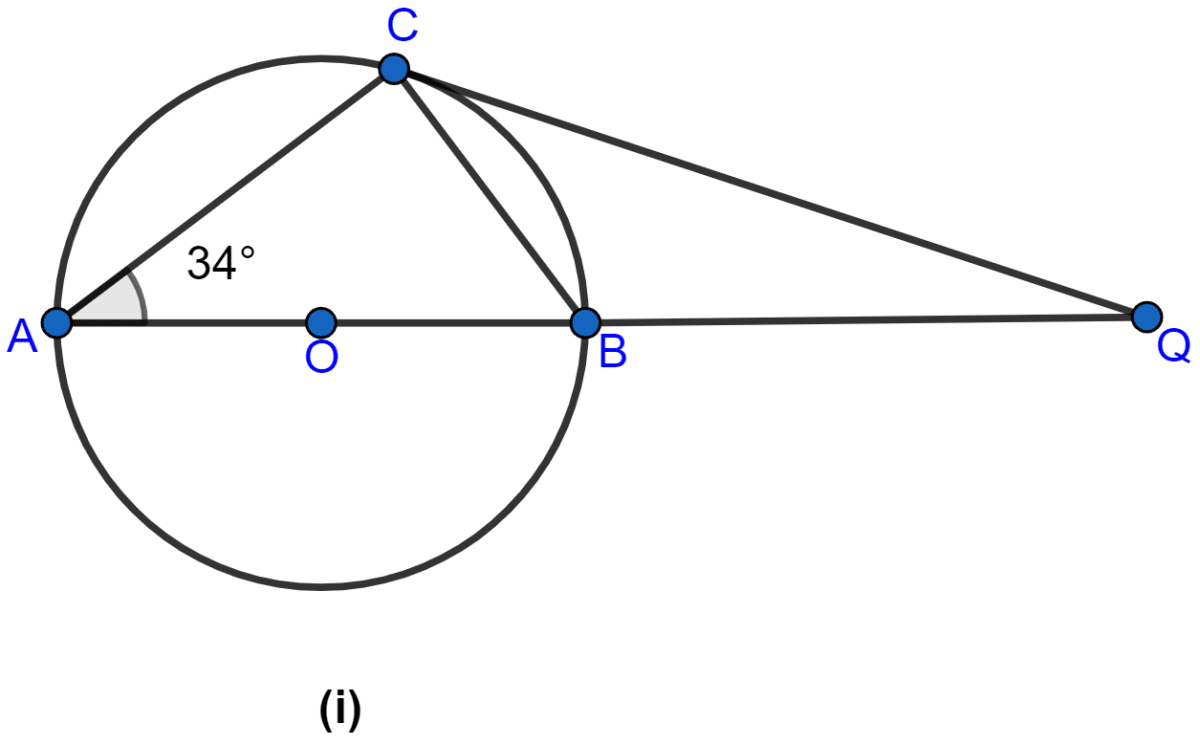
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA