Mathematics
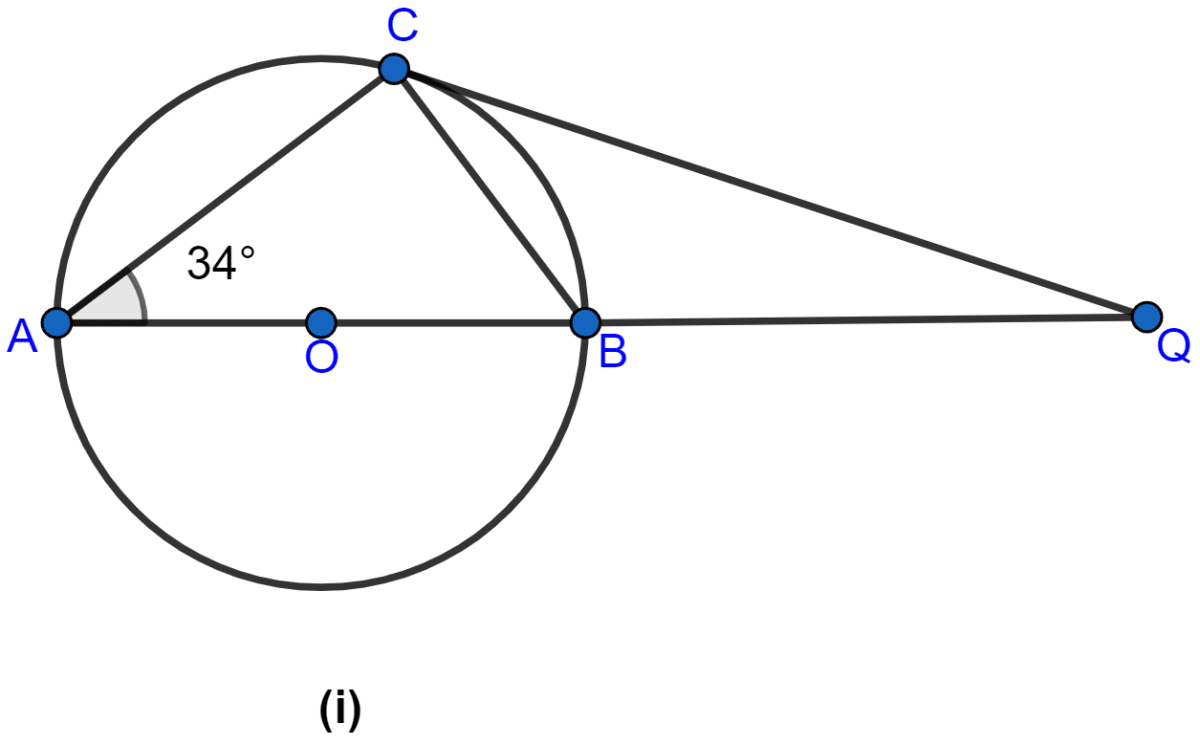
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA
Circles
31 Likes
Answer
From figure,
∠ACB = 90 (∵ angles in semicircle is equal to 90.)
Since sum of angles in a triangle = 180.
In △ABC,
⇒ ∠CAB + ∠ACB + ∠CBA = 180°
⇒ 34° + 90° + ∠CBA = 180°
⇒ 124° + ∠CBA = 180°
⇒ ∠CBA = 180° - 124°
⇒ ∠CBA = 56°.
Hence, the value of ∠CBA = 56°.
(ii) From figure,
∠BCQ = ∠CAB = 34°. (∵ angles in alternate segments are equal.)
∠ACQ = ∠ACB + ∠BCQ = 90° + 34° = 124°.
Since sum of angles in a triangle = 180°.
In △ACQ,
⇒ ∠CAQ + ∠ACQ + ∠CQA = 180°
⇒ 34° + 124° + ∠CQA = 180°
⇒ 158° + ∠CQA = 180°
⇒ ∠CQA = 180° - 158°
⇒ ∠CQA = 22°.
Hence, the value of ∠CQA = 22°.
Answered By
25 Likes
Related Questions
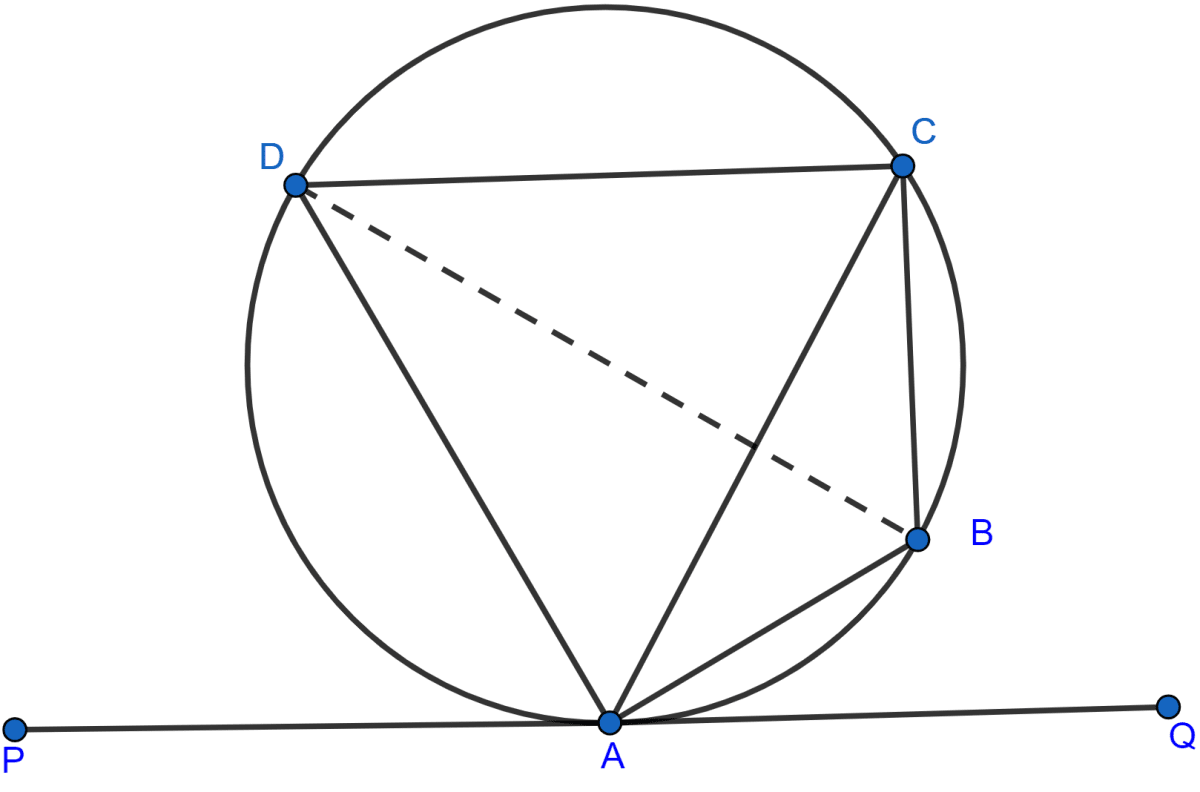
In the adjoining figure, ABCD is a cyclic quadrilateral. The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measures of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate :
(i) ∠QOR
(ii) ∠QPR, given that ∠A = 60°.
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate :
(i) ∠AOB
(ii) ∠OAB
(iii) ∠ACB

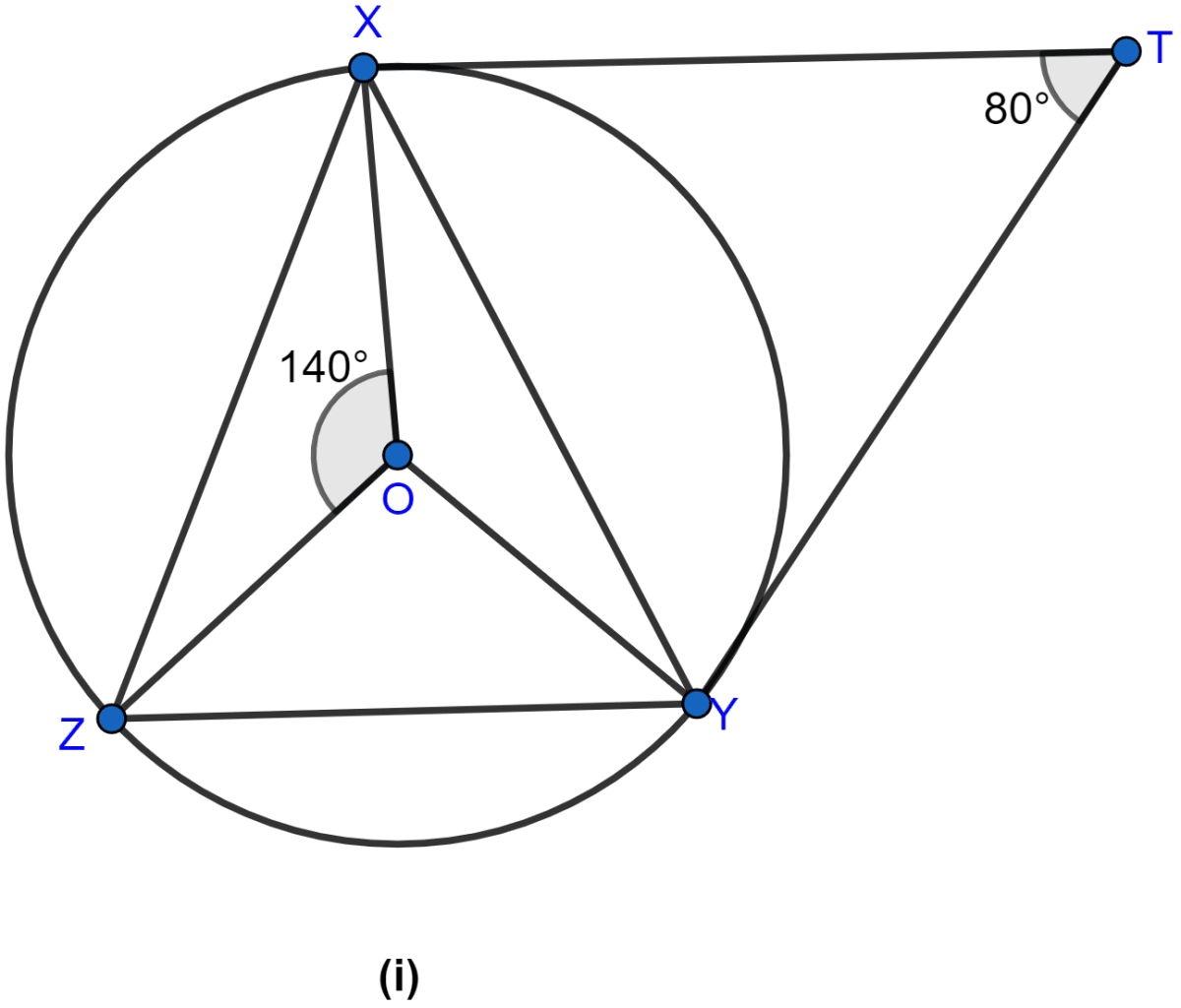
In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.