Mathematics
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate :
(i) ∠QOR
(ii) ∠QPR, given that ∠A = 60°.
Circles
21 Likes
Answer
(i) From figure,

OQ ⊥ AC and OR ⊥ AB (∵ OQ and OR are the radii and AC and AB are tangents.)
Now in quadrilateral AROQ,
∠A = 60°, ∠ORA = 90° and ∠OQA = 90°.
∠A + ∠ORA + ∠OQA + ∠QOR = 360°
60° + 90° + 90° + ∠QOR = 360°
240° + ∠QOR = 360°
∠QOR = 360° - 240°
∠QOR = 120°.
Hence, the value of ∠QOR = 120°.
(ii) Arc QR subtends ∠QOR at the centre and ∠QPR at the remaining part of the circle.
∴ ∠QOR = 2∠QPR (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle)
120° = 2∠QPR
∠QPR = = 60°.
Hence, the value of ∠QPR = 60°.
Answered By
11 Likes
Related Questions
In the figure (ii) given below, O is the centre of the circle. AB is a diameter, TPT' is a tangent to the circle at P. If ∠BPT' = 30°, calculate
(i) ∠APT
(ii) ∠BOP

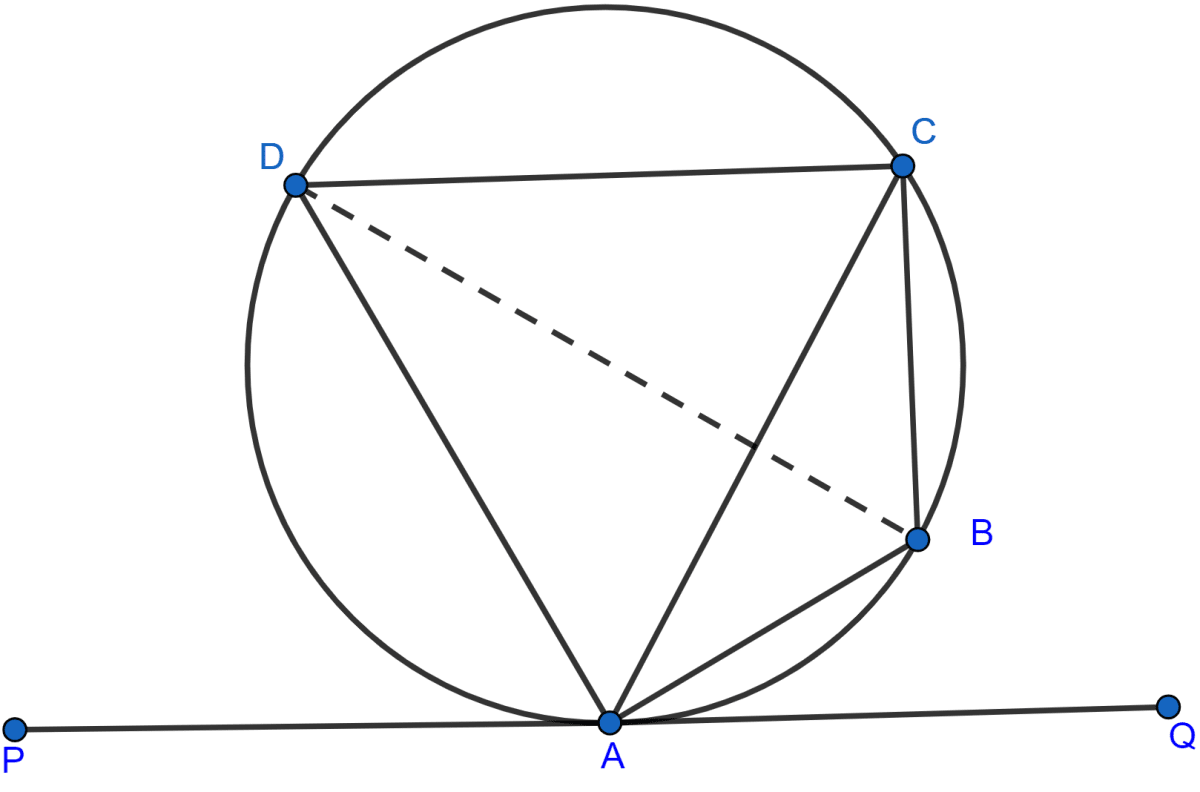
In the adjoining figure, ABCD is a cyclic quadrilateral. The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measures of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
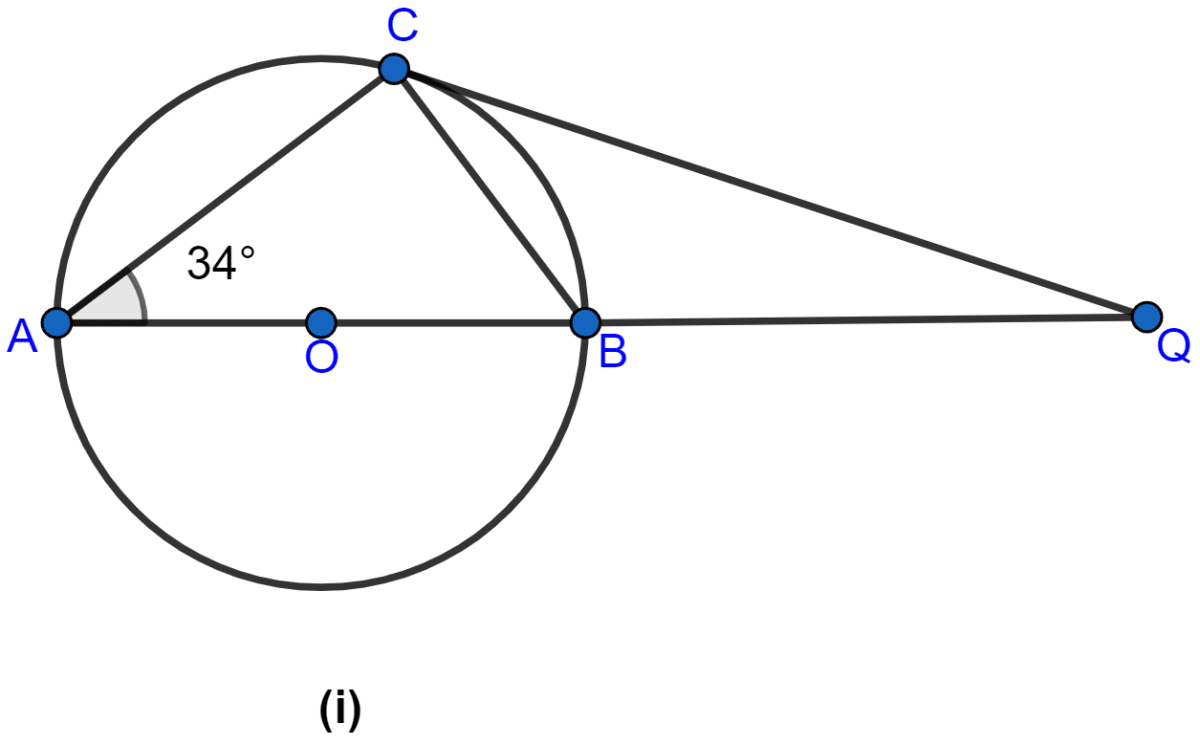
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate :
(i) ∠AOB
(ii) ∠OAB
(iii) ∠ACB
