Mathematics
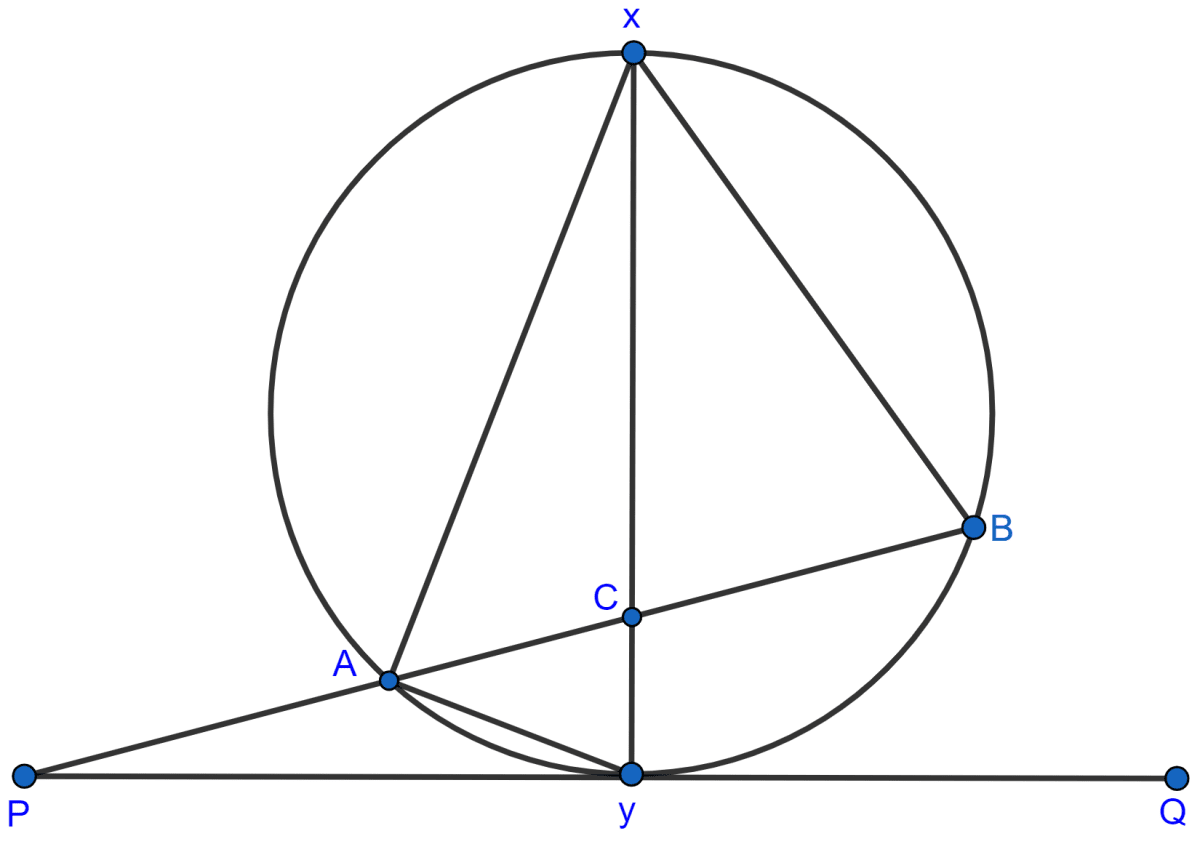
Chords AB and CD of a circle when extended meet at point X. Given AB = 4 cm, BX = 6 cm and XD = 5 cm, calculate the length of CD.
Circles
3 Likes
Answer
Chords AB and CD of the circle meeting at point X are shown below:

We know that,
If two chords of a circle intersect internally or externally then the product of the lengths of their segments is equal.
⇒ XB.XA = XD.XC
⇒ 6.(6 + 4) = 5.(5 + CD)
⇒ 6 × 10 = 25 + 5CD
⇒ 5CD = 60 - 25
⇒ 5CD = 35
⇒ CD =
⇒ CD = 7 cm.
Hence, CD = 7 cm.
Answered By
3 Likes
Related Questions
The given figure shows a circle with center O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate :
(i) angle QTR
(ii) angle QRP
(iii) angle QRS
(iv) angle STR

TA and TB are tangents to a circle with center O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
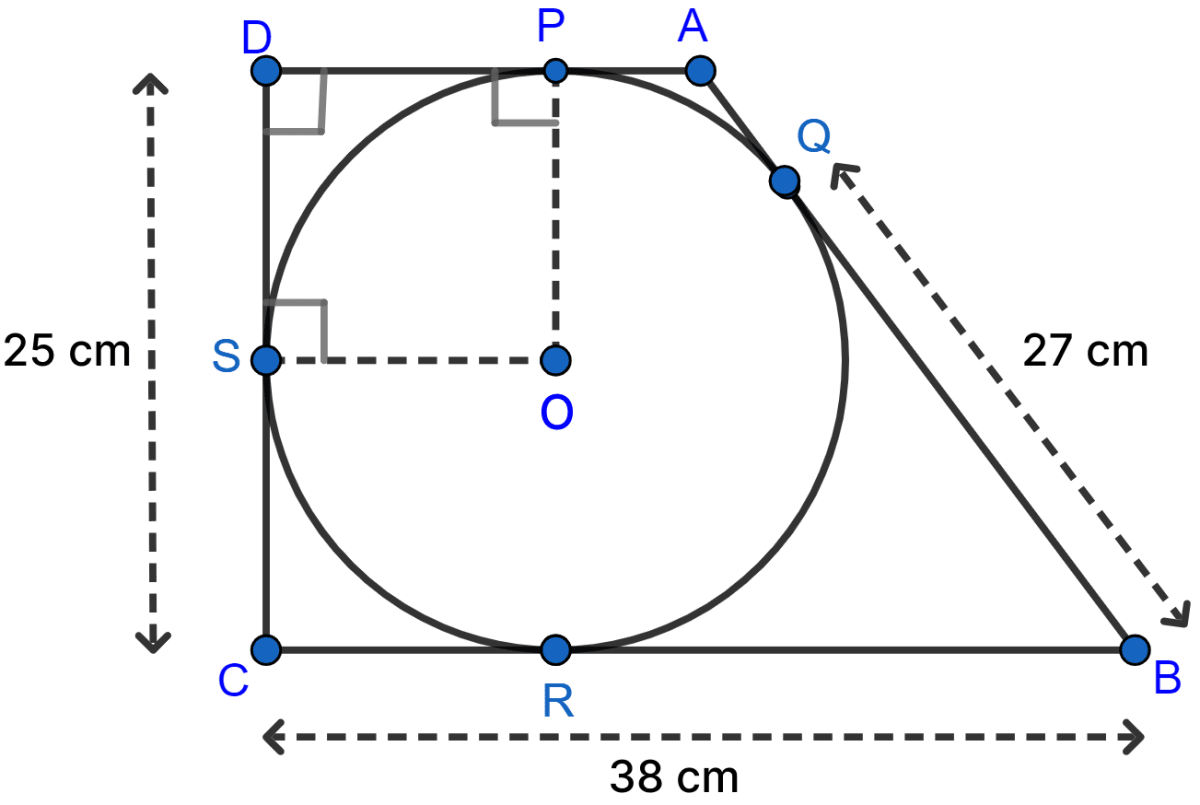
In the following figure, a circle is inscribed in the quadrilateral ABCD. If BC = 38 cm, QB = 27 cm, DC = 25 cm and that AD is perpendicular to DC, find the radius of the circle.
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.