Mathematics
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if :
(i) they touch each other externally,
(ii) they touch each other internally.
Answer
Let O be the center of the circle with radius = 6.3 cm and O' be the center of circle with radius = 3.6 cm.
(i) When the two circles touch each other at P externally. O' and O are the centers of the circles. Join O'P and OP.

So, O'P = 6.3 cm, OP = 3.6 cm
Hence, the distance between their centres (O'O) is given by
O'O = O'P + OP = 6.3 + 3.6 = 9.9 cm.
Hence, distance between their centers if they touch each other externally is 9.9 cm.
(ii) When the two circles touch each other at P internally, O and O' are the centers of the circles. Join OP and O'P.
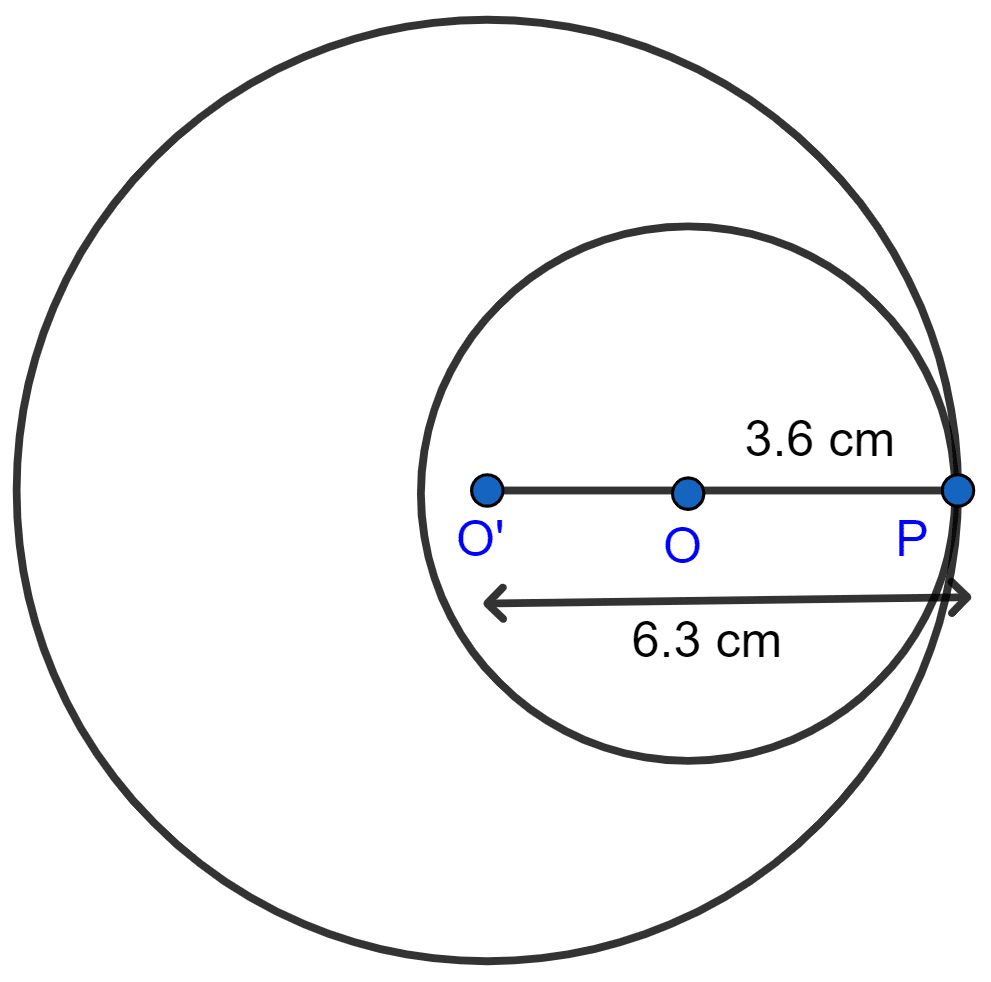
So, O'P = 6.3 cm, OP = 3.6 cm.
Hence, the distance between their centres (O'O) is given by
O'O = O'P - OP = 6.3 - 3.6 = 2.7 cm.
Hence, distance between their centers if they touch each other internally is 2.7 cm.
Related Questions
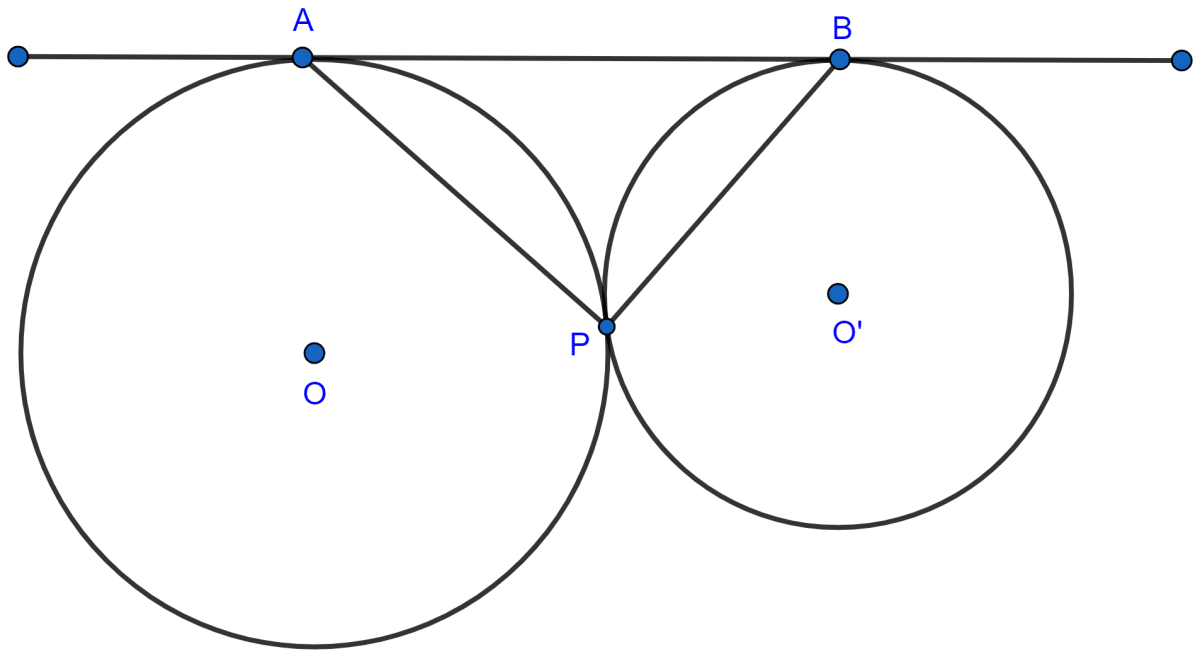
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
(i) tangent at point P bisects AB.
(ii) angle APB = 90°.
From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP
(ii) OP is the ⊥ bisector of chord AB.
In the given figure, if AB = AC then prove that BQ = CQ.
