Mathematics
From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP
(ii) OP is the ⊥ bisector of chord AB.
Circles
3 Likes
Answer
The circle with centre O and tangents PA and PB drawn from point P outside the circle is shown in the below figure:
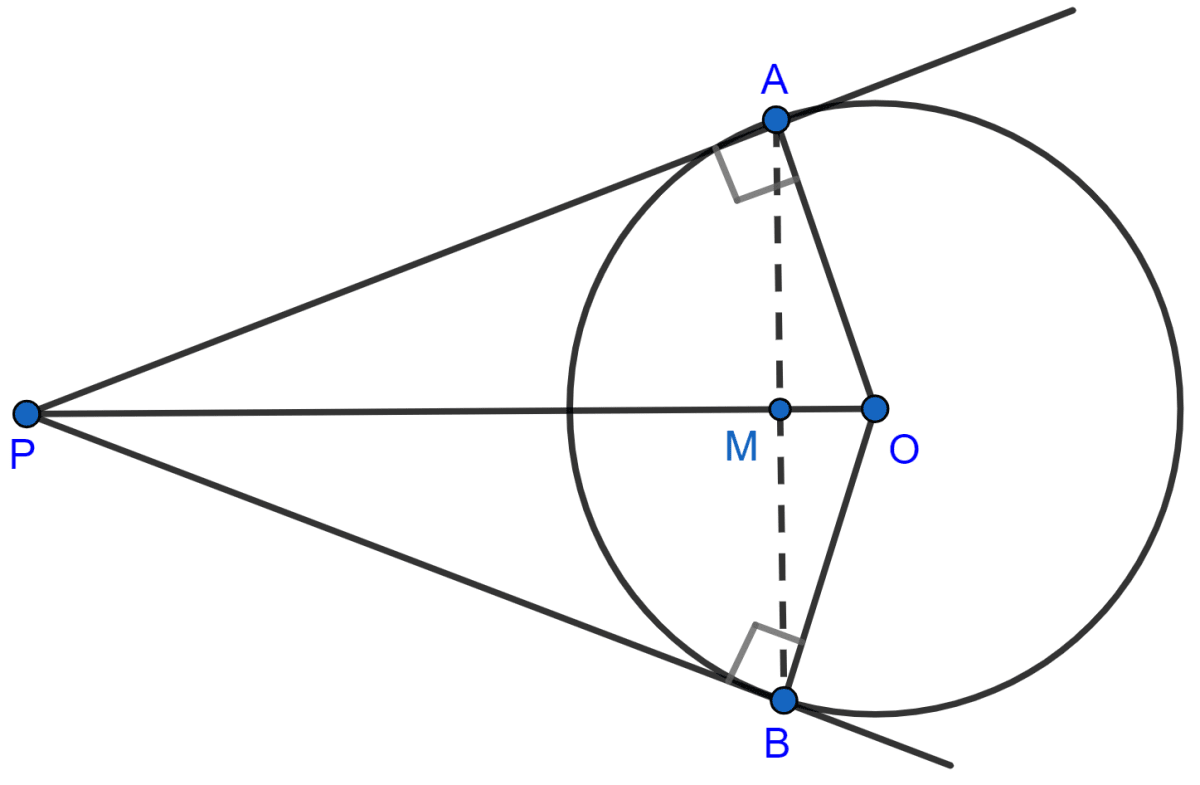
(i) In ∆AOP and ∆BOP, we have
⇒ AP = BP [Tangents from an exterior point P, are equal in length.]
⇒ OA = OB [Radius of circle]
⇒ OP = OP [Common]
∴ ΔAOP ≅ ΔBOP by SSS axiom.
∴ ∠AOP = ∠BOP [By C.P.C.T.]
Hence, proved that ∠AOP = ∠BOP.
(ii) In ∆OAM and ∆OBM, we have
OA = OB [Radii of the same circle]
∠AOM = ∠BOM [Proved ∠AOP = ∠BOP]
OM = OM [Common]
∴ ΔOAM ≅ ΔOBM [By SAS axiom]
By C.P.C.T.
⇒ AM = MB and ∠OMA = ∠OMB = x
From figure,
⇒ ∠OMA + ∠OMB = 180° [As, AB is a straight line]
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x =
⇒ x = 90°.
Thus, ∠OMA = ∠OMB = 90°.
Hence proved, that OP is the ⊥ bisector of chord AB.
Answered By
2 Likes
Related Questions
Tangents AP and AQ are drawn to a circle, with center O, from an exterior point A. Prove that :
∠PAQ = 2∠OPQ
In the given figure, if AB = AC then prove that BQ = CQ.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if :
(i) they touch each other externally,
(ii) they touch each other internally.
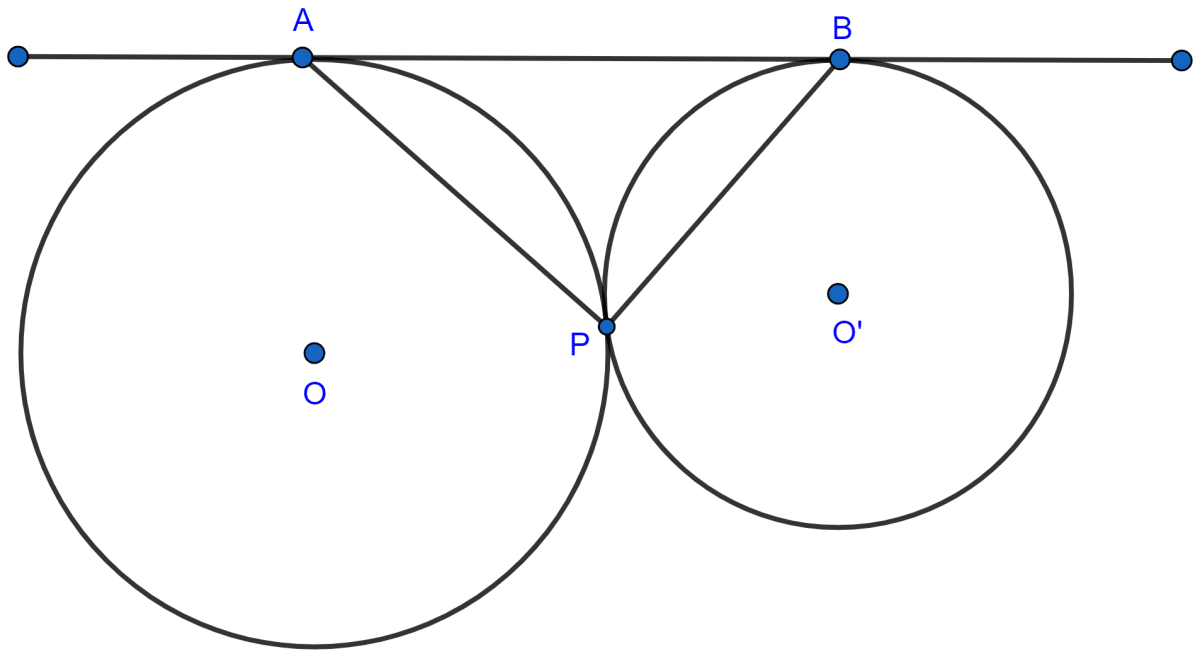
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
(i) tangent at point P bisects AB.
(ii) angle APB = 90°.
