Mathematics
Tangents AP and AQ are drawn to a circle, with center O, from an exterior point A. Prove that :
∠PAQ = 2∠OPQ
Circles
4 Likes
Answer
We know that,
The tangent at any point of a circle and the radius through this point are perpendicular to each other.
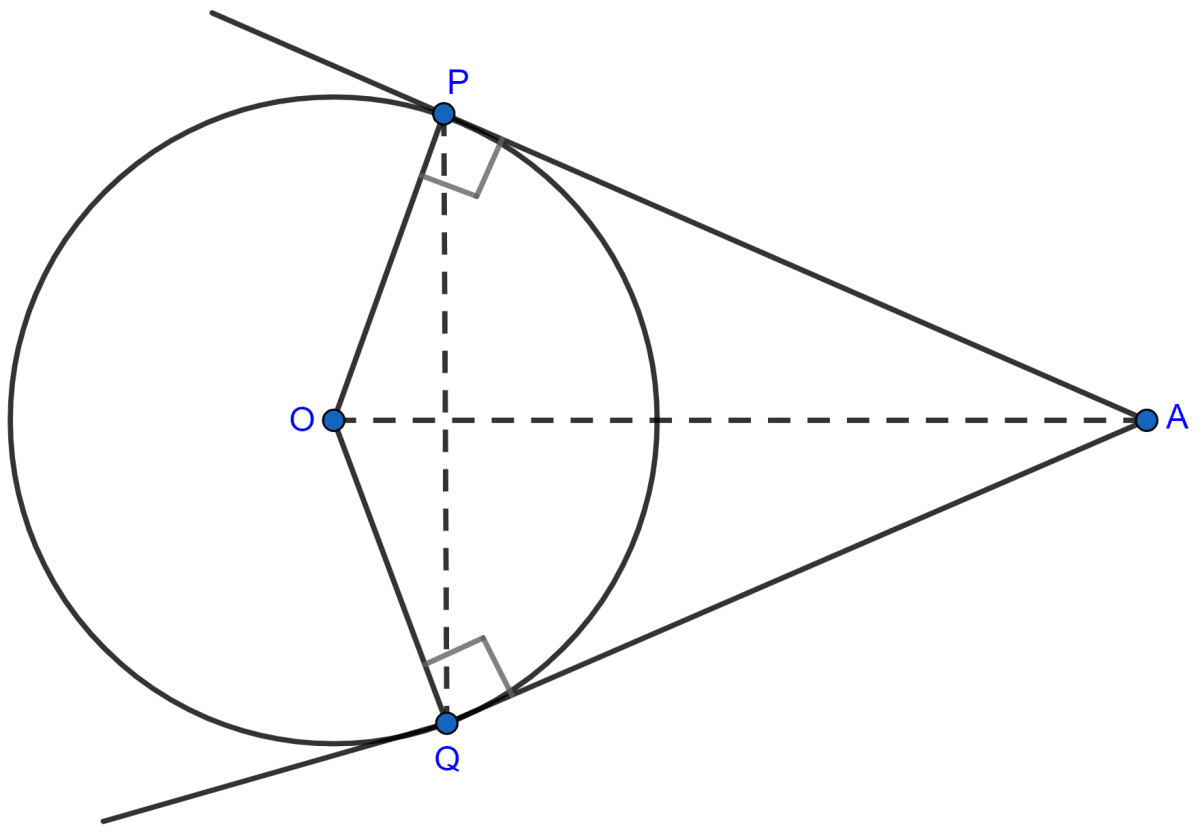
In quadrilateral OPAQ,
∠OPA = ∠OQA = 90°.
∠OPA + ∠OQA + ∠POQ + ∠PAQ = 360° [∵ Sum of angles in quadrilateral = 360°]
90° + 90° + ∠POQ + ∠PAQ = 360°
∠POQ + ∠PAQ = 360° - 180°
∠POQ + ∠PAQ = 180° ……….(1)
In △OPQ,
OP = OQ [Radius of same circle]
∴ ∠OPQ = ∠OQP [Angles opposite to equal sides are equal]
By angle sum property of triangle,
⇒ ∠OPQ + ∠OQP + ∠POQ = 180°
⇒ ∠OPQ + ∠OPQ + ∠POQ = 180°
⇒ 2∠OPQ + ∠POQ = 180° ………(2)
From (1) and (2) we get,
∠POQ + ∠PAQ = 2∠OPQ + ∠POQ
⇒ ∠PAQ = 2∠OPQ.
Hence, proved that ∠PAQ = 2∠OPQ.
Answered By
2 Likes
Related Questions
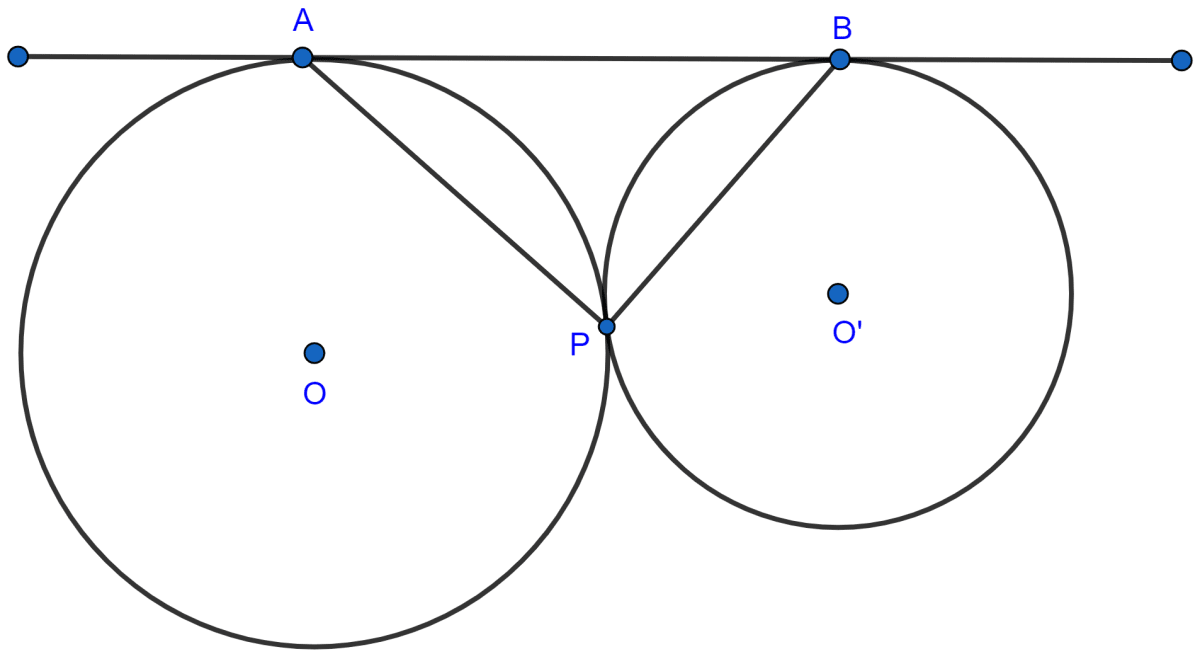
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
(i) tangent at point P bisects AB.
(ii) angle APB = 90°.
From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP
(ii) OP is the ⊥ bisector of chord AB.
In a triangle ABC, the incircle (center O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
(i) ∠QOR
(ii) ∠QPR;
given that ∠A = 60°.
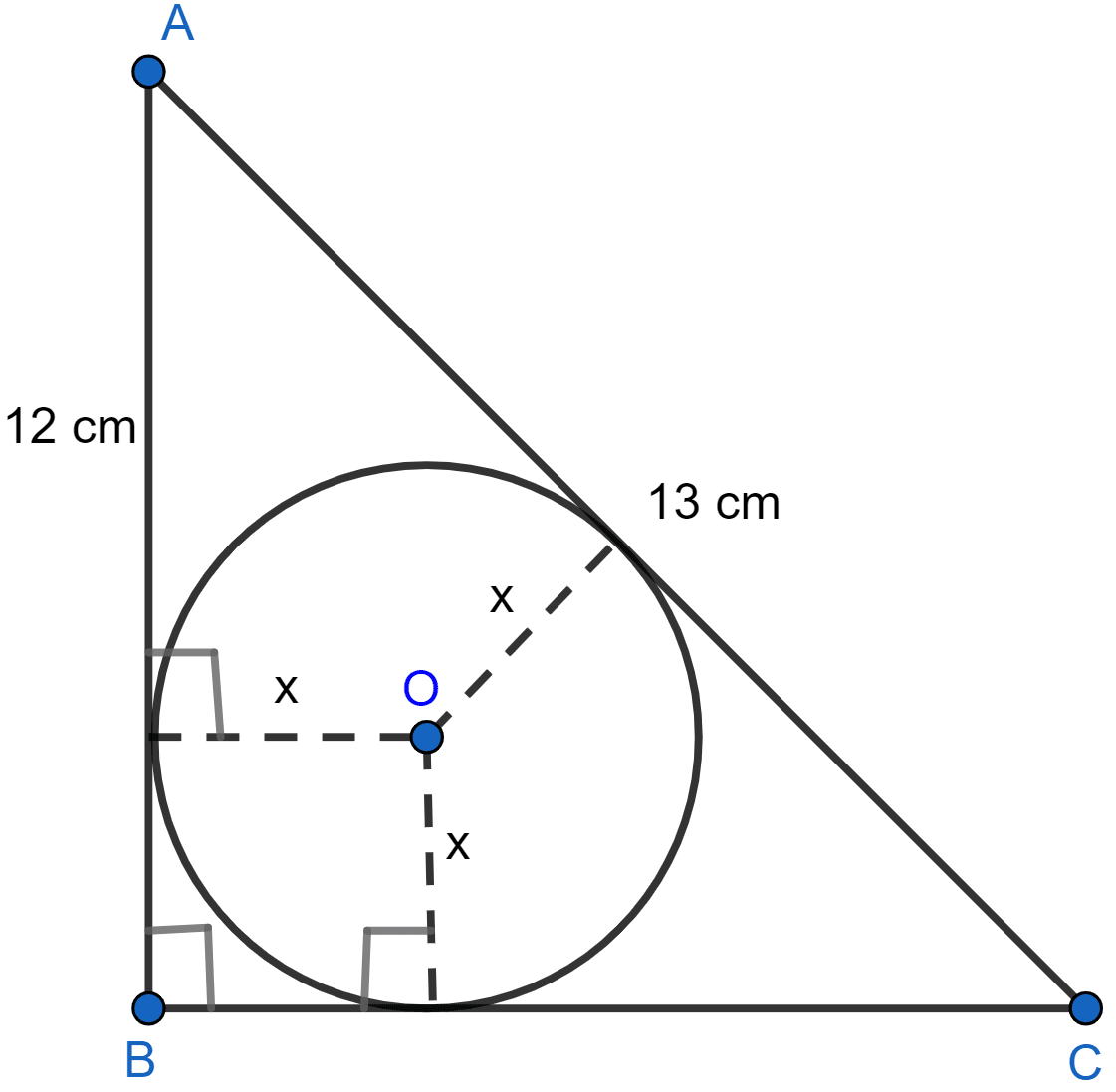
ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with center O, has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
