Mathematics
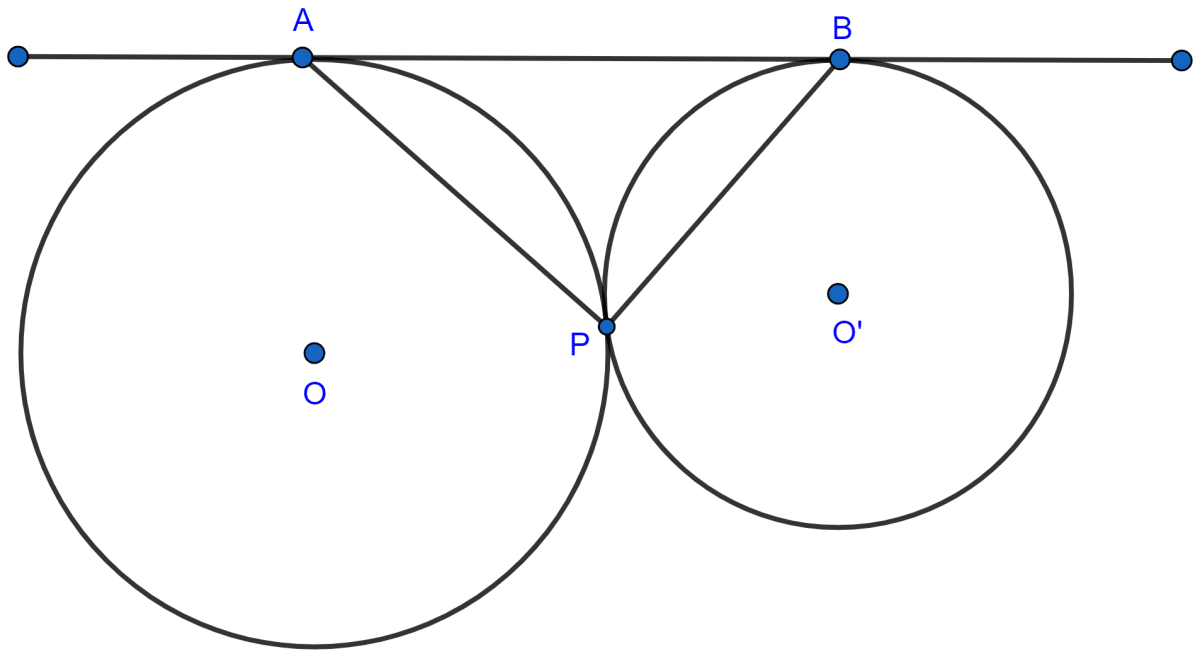
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
(i) tangent at point P bisects AB.
(ii) angle APB = 90°.
Circles
4 Likes
Answer
(i) We know that,
If two tangents are drawn to a circle from an exterior point, the tangents are equal in length.
From figure,
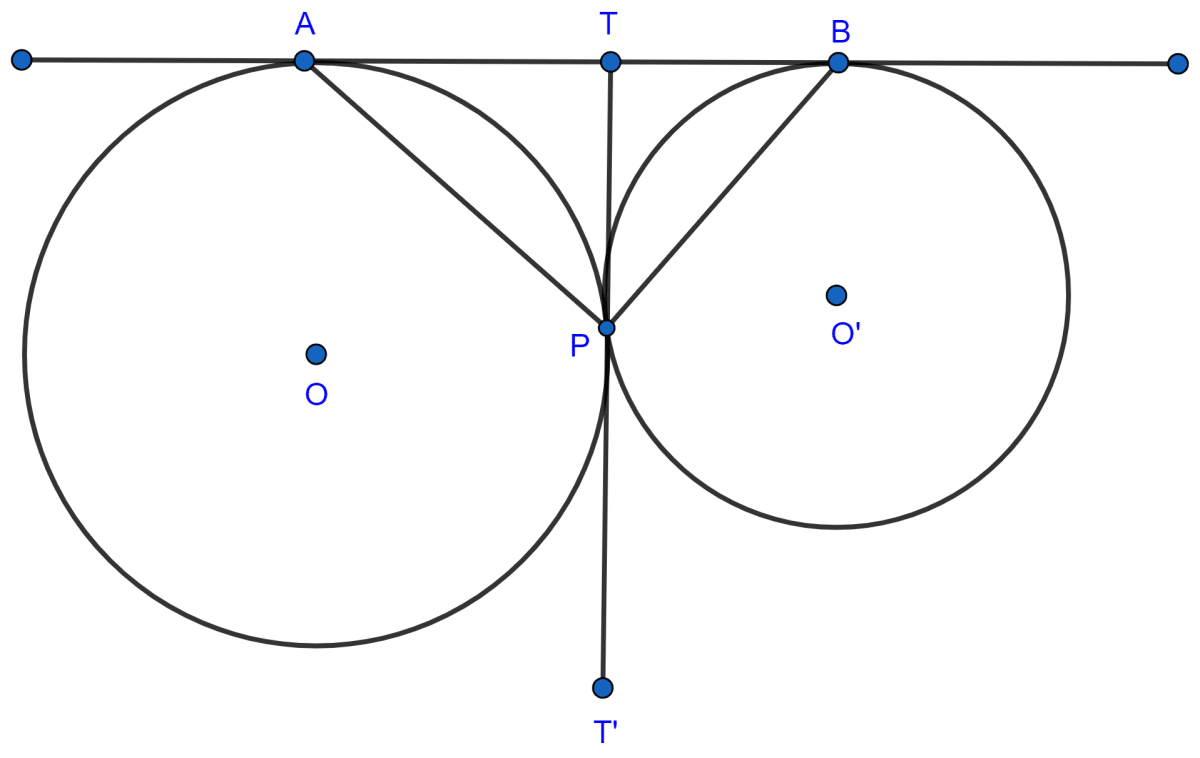
TA and TP are the tangents to the circle with center O.
∴ TA = TP ………..(1)
TB and TP are the tangents to the circle with center O'.
∴ TB = TP ………..(2)
From (1) and (2) we get :
TA = TB.
Hence, proved that tangent at point P bisects AB.
(ii) In △ATP,
TA = TP [Proved above]
∴ ∠TAP = ∠TPA ………(1) [∵ angles opposite to equal sides are equal.]
In △BTP,
TB = TP [Proved above]
∴ ∠TBP = ∠TPB ……….(2) [∵ angles opposite to equal sides are equal.]
Adding (1) and (2), we get :
∠TAP + ∠TBP = ∠TPA + ∠TPB
∠TAP + ∠TBP = ∠APB ………..(3)
In △ABP,
⇒ ∠APB + ∠BAP + ∠ABP = 180° [Angle sum property of triangle]
⇒ ∠APB + ∠TAP + ∠TBP = 180° [From figure, ∠TAP = ∠BAP and ∠TBP = ∠ABP.]
⇒ ∠APB + ∠APB = 180°
⇒ 2∠APB = 180°
⇒ ∠APB = 90°.
Hence, proved that ∠APB = 90°.
Answered By
3 Likes
Related Questions
Tangents AP and AQ are drawn to a circle, with center O, from an exterior point A. Prove that :
∠PAQ = 2∠OPQ
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if :
(i) they touch each other externally,
(ii) they touch each other internally.
From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP
(ii) OP is the ⊥ bisector of chord AB.
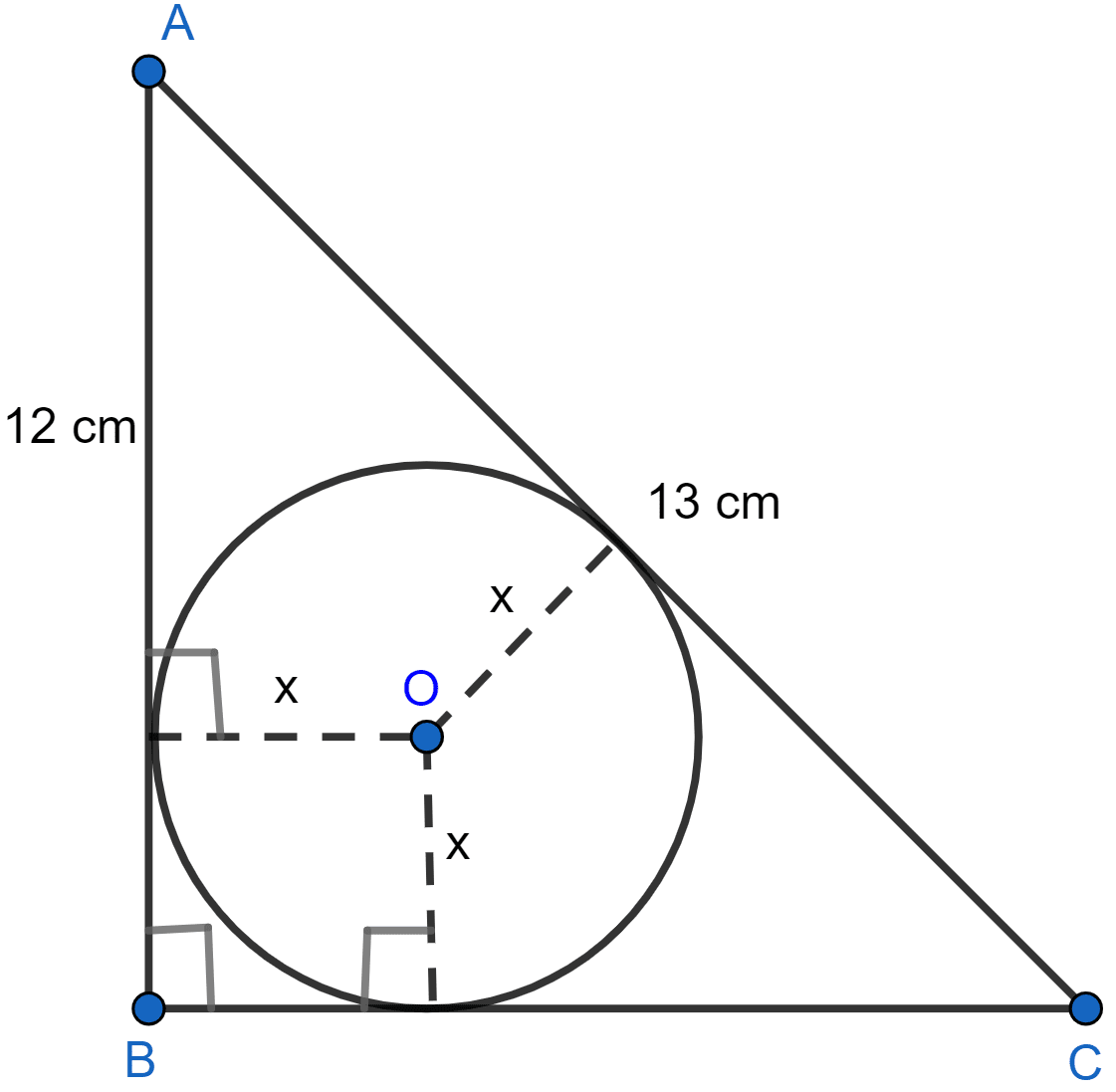
ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with center O, has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
