Mathematics
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if :
(i) they touch each other externally,
(ii) they touch each other internally.
Circles
21 Likes
Answer
Let O be the center of the circle with radius = 6.3 cm and O' be the center of circle with radius = 3.6 cm.
(i) When the two circles touch each other at P externally. O' and O are the centers of the circles. Join O'P and OP.

So, O'P = 6.3 cm, OP = 3.6 cm
Hence, the distance between their centres (O'O) is given by
O'O = O'P + OP = 6.3 + 3.6 = 9.9 cm.
Hence, distance between their centers if they touch each other externally is 9.9 cm.
(ii) When the two circles touch each other at P internally, O and O' are the centers of the circles. Join OP and O'P.
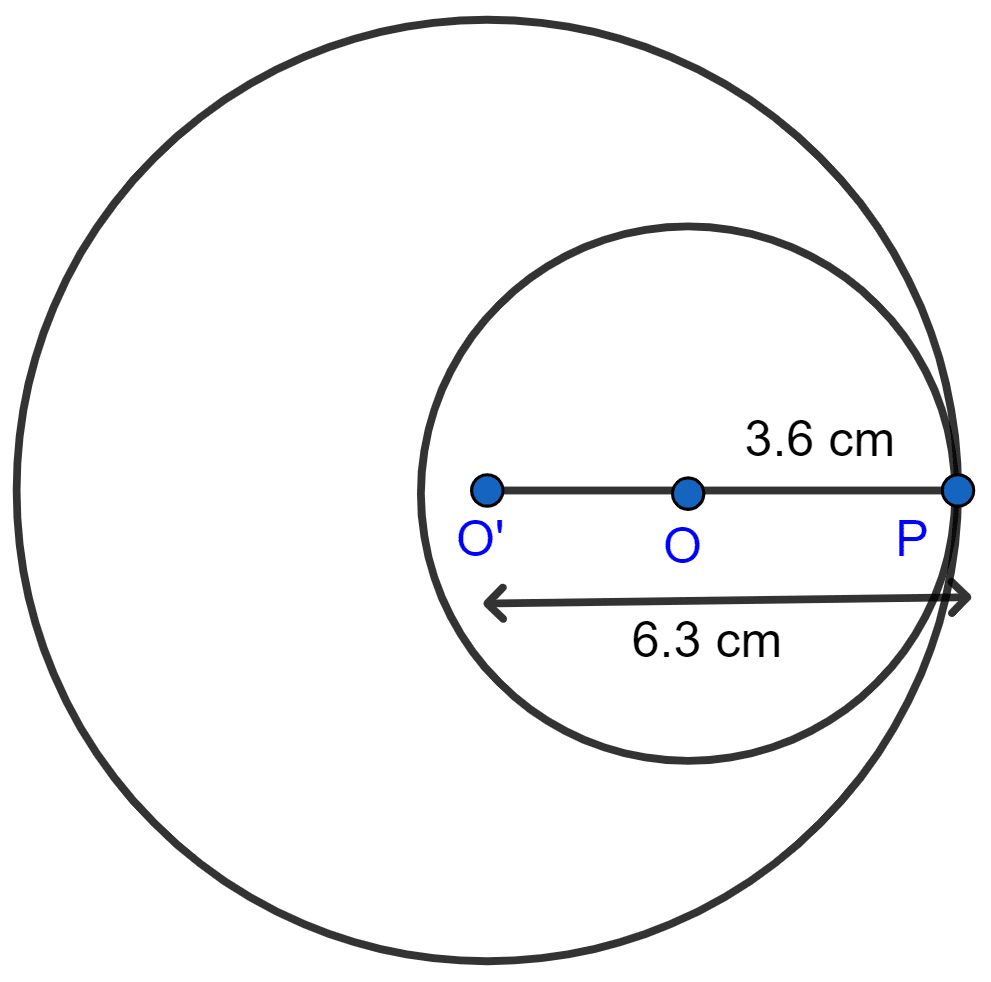
So, O'P = 6.3 cm, OP = 3.6 cm.
Hence, the distance between their centres (O'O) is given by
O'O = O'P - OP = 6.3 - 3.6 = 2.7 cm.
Hence, distance between their centers if they touch each other internally is 2.7 cm.
Answered By
12 Likes
Related Questions
From the given figure, prove that :
AP + BQ + CR = BP + CQ + AR.
Also, show that :
AP + BQ + CR = x Perimeter of triangle ABC.

In the given figure, if AB = AC then prove that BQ = CQ.

From a point P outside the circle, with centre O, tangents PA and PB are drawn. Prove that:
(i) ∠AOP = ∠BOP
(ii) OP is the ⊥ bisector of chord AB.
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that :
(i) tangent at point P bisects AB.
(ii) angle APB = 90°.