Mathematics
Prove that the diagonals of a parallelogram divide it into four triangles of equal area.
Theorems on Area
24 Likes
Answer
Let us consider a parallelogram ABCD, the diagonals AC and BD cut at point O.

In parallelogram ABCD, the diagonals bisect each other.
AO = OC
In ∆ACD, O is the mid-point of AC.
∴ OD is the median.
Area of ∆AOD = Area of ∆COD ……. (i) [Median of ∆ divides it into two triangles of equal areas.]
Similarly, in ∆ABC
O is the mid-point of AC.
∴ OB is the median.
Area of ∆AOB = Area of ∆COB ……. (ii) [Median of ∆ divides it into two triangles of equal areas.]
In ∆ADB,
O is the mid-point of BD.
∴ OA is the median.
Area of ∆AOD = Area of ∆AOB ……. (iii)
From (i), (ii) and (iii) we get,
Area of ∆AOB = ∆COB = ∆COD = ∆AOD
Hence proved, that the diagonals of a parallelogram divide it into four triangles of equal area.
Answered By
16 Likes
Related Questions
Prove that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
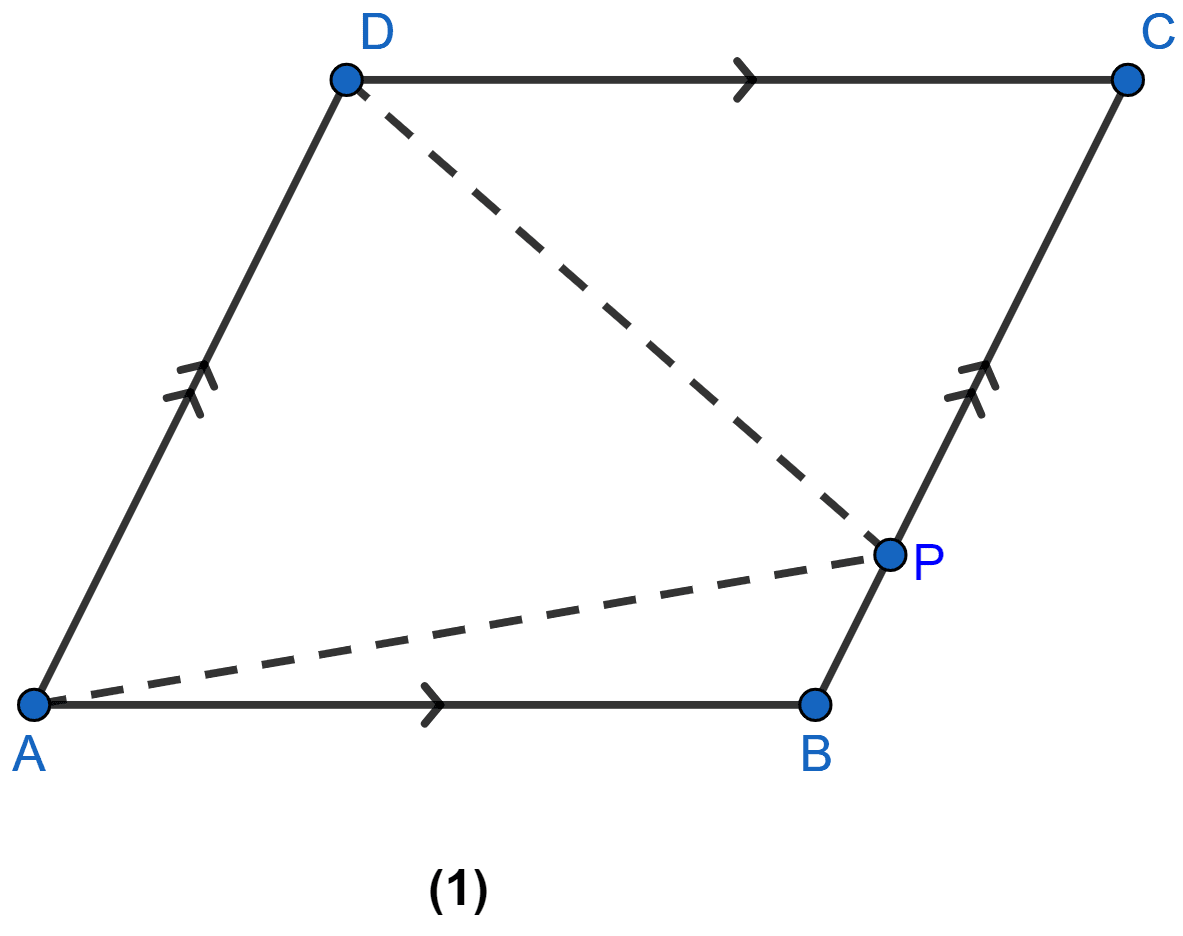
In figure (1) given below, ABCD is a parallelogram and P is any point in BC. Prove that, Area of ∆ABP + area of ∆DPC = Area of ∆APD.
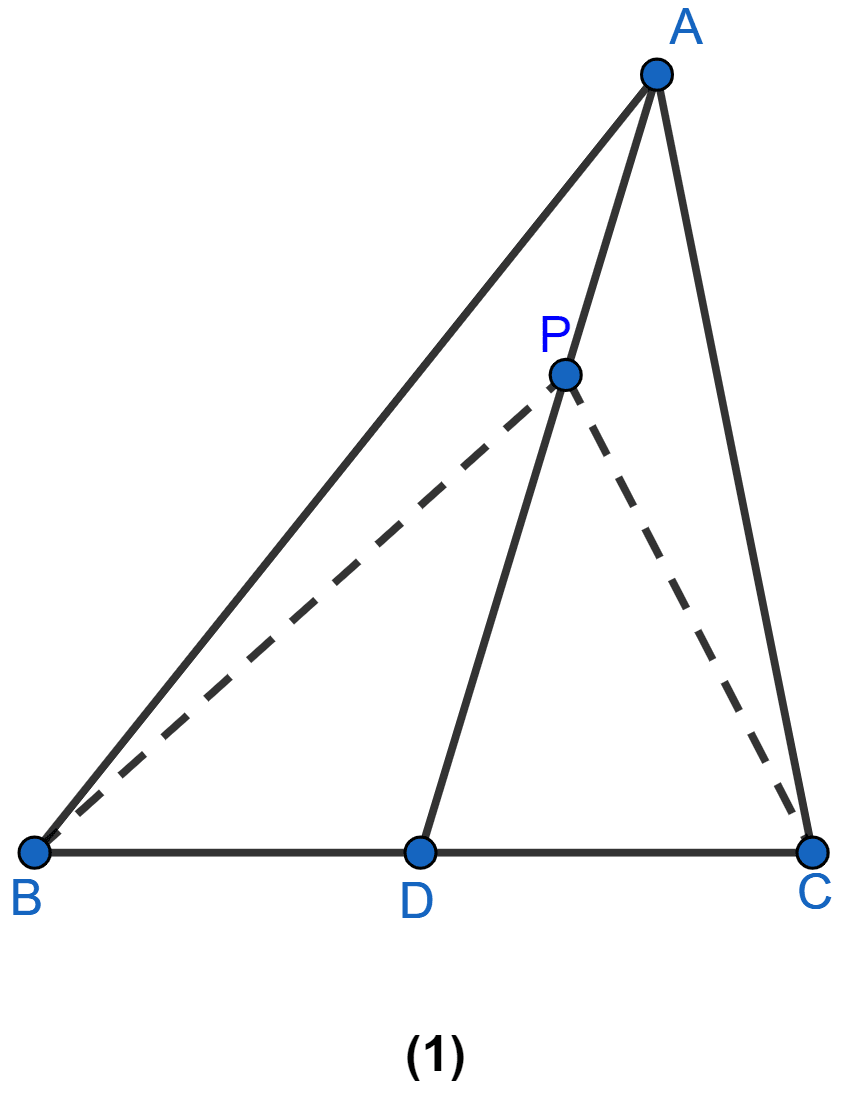
In figure (1) given below, AD is the median of ∆ABC and P is any point on AD. Prove that
(i) Area of ∆PBD = area of ∆PDC.
(ii) Area of ∆ABP = area of ∆ACP.
In the figure (2) given below, DE || BC. Prove that
(i) area of ∆ACD = area of ∆ABE
(ii) area of ∆OBD = area of ∆OCE.
