Mathematics
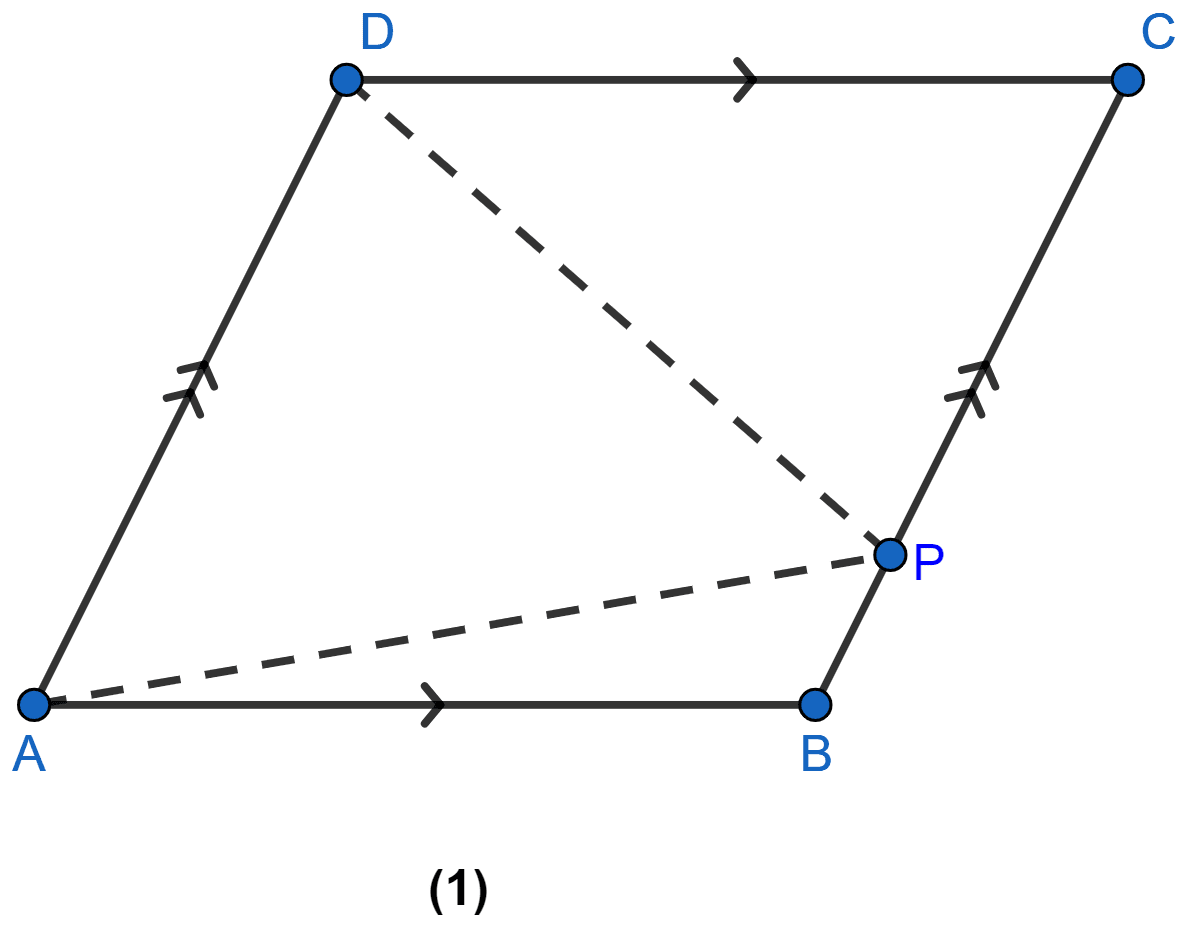
In figure (1) given below, ABCD is a parallelogram and P is any point in BC. Prove that, Area of ∆ABP + area of ∆DPC = Area of ∆APD.
Theorems on Area
39 Likes
Answer
We know that,
Area of a triangle is half that of a parallelogram on the same base and between the same parallel lines.
∆APD and || gm ABCD are on the same base AD and between the same || lines AD and BC,
∴ Area of ∆APD = Area of || gm ABCD …….(i)
From figure,
Area of ||gm ABCD = Area of ∆APD + Area of ∆ABP + Area of ∆DPC
Dividing the above equation by 2 we get,
From (i),
Hence, proved that Area of ∆APD = Area of ∆ABP + Area of ∆DPC.
Answered By
20 Likes
Related Questions
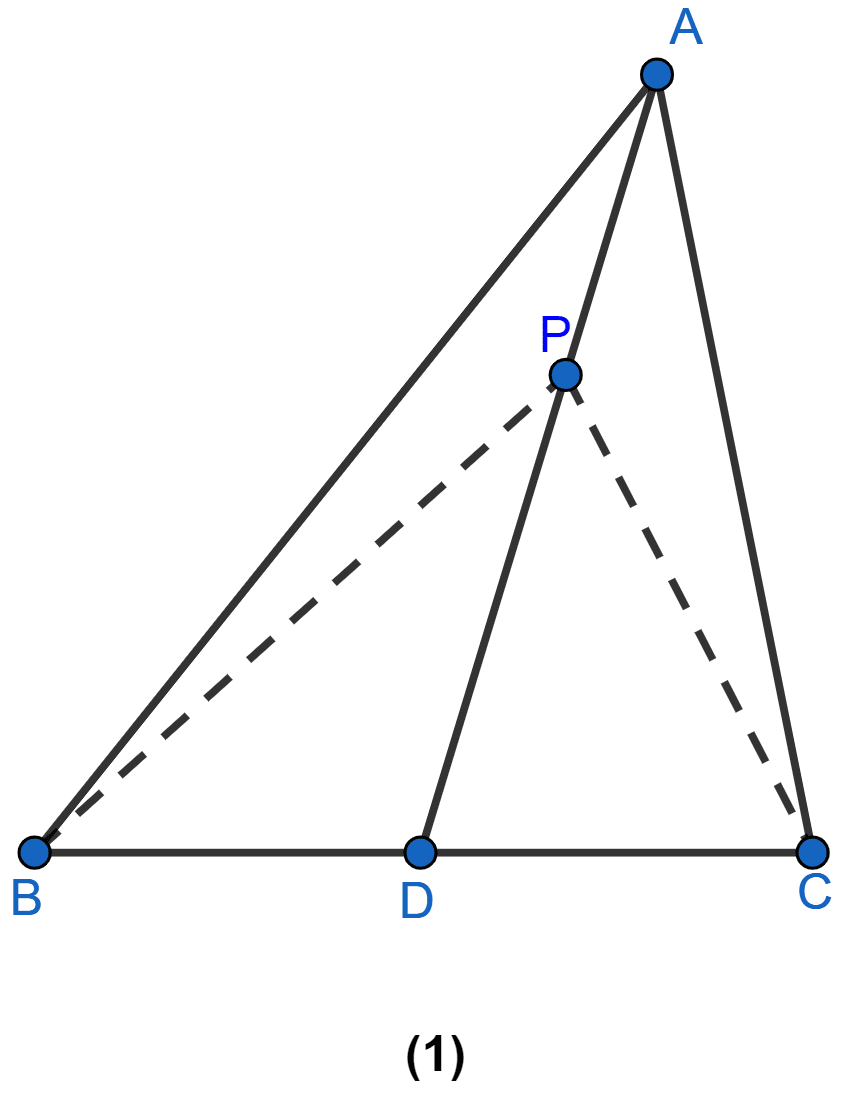
In figure (1) given below, AD is the median of ∆ABC and P is any point on AD. Prove that
(i) Area of ∆PBD = area of ∆PDC.
(ii) Area of ∆ABP = area of ∆ACP.
In the figure (2) given below, DE || BC. Prove that
(i) area of ∆ACD = area of ∆ABE
(ii) area of ∆OBD = area of ∆OCE.

In the figure (2) given below, O is any point inside a parallelogram ABCD. Prove that
(i) area of ∆OAB + area of ∆OCD = area of || gm ABCD.
(ii) area of ∆OBC + area of ∆OAD = area of || gm ABCD.

If E, F, G and H are mid-points of the sides AB, BC, CD and DA, respectively of a parallelogram ABCD, prove that area of the quad. EFGH = area of || gm ABCD.