Mathematics
In the figure (2) given below, O is any point inside a parallelogram ABCD. Prove that
(i) area of ∆OAB + area of ∆OCD = area of || gm ABCD.
(ii) area of ∆OBC + area of ∆OAD = area of || gm ABCD.

Theorems on Area
19 Likes
Answer
(i) Draw a line PQ || to AB and CD from point O.

AB || PQ and AP || BQ (Since, AD || BC)
ABQP is a || gm
Similarly,
PD || CQ and PQ || DC
PQCD is a || gm
Now, ∆OAB and || gm ABQP are on the same base AB and between same || lines AB and PQ
Area of ∆OAB = Area of ||gm ABQP …..(1)
Similarly, ∆OCD and || gm PQCD are on the same base CD and between same || lines CD and PQ
Area of ∆OCD = Area of || gm PQCD ….. (2)
Now by adding (1) and (2),
Area of ∆OAB + Area of ∆OCD = Area of || gm ABQP + Area of || gm PQCD
= [Area of || gm ABQP + Area of || gm PQCD]
= Area of || gm ABCD
Hence, proved that Area of ∆OAB + Area of ∆OCD = Area of || gm ABCD.
(ii) From figure,
⇒ Area of ∆OAB + Area of ∆OBC + Area of ∆OCD + Area of ∆OAD = Area of || gm ABCD
⇒ Area of ∆OAB + Area of ∆OCD + Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD
⇒ Area of || gm ABCD + Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD
⇒ Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD - Area of || gm ABCD
⇒ Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD.
Hence, proved that Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD.
Answered By
13 Likes
Related Questions
In the figure (2) given below, DE || BC. Prove that
(i) area of ∆ACD = area of ∆ABE
(ii) area of ∆OBD = area of ∆OCE.

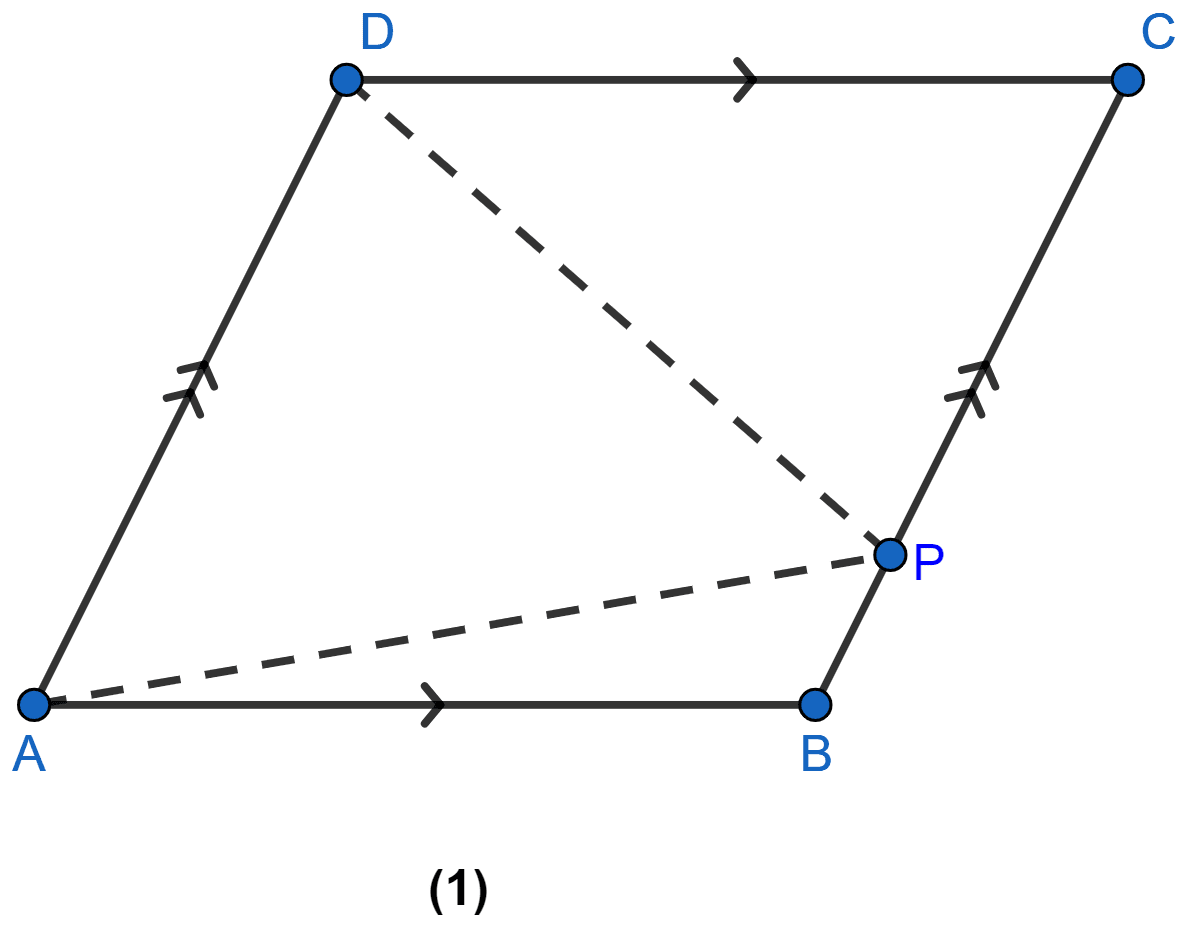
In figure (1) given below, ABCD is a parallelogram and P is any point in BC. Prove that, Area of ∆ABP + area of ∆DPC = Area of ∆APD.
If E, F, G and H are mid-points of the sides AB, BC, CD and DA, respectively of a parallelogram ABCD, prove that area of the quad. EFGH = area of || gm ABCD.
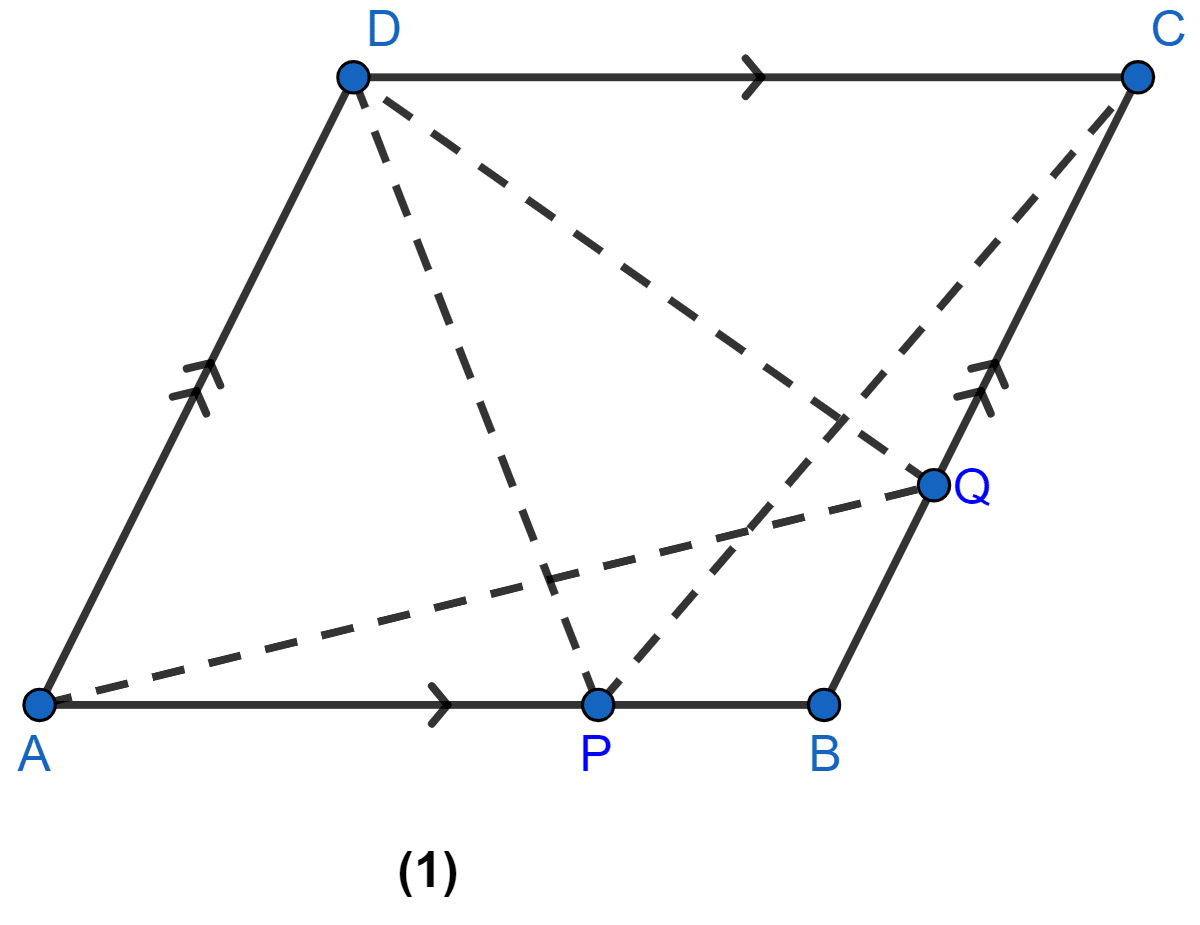
In figure (1) given below, ABCD is a parallelogram. P, Q are any two points on the sides AB and BC respectively. Prove that
area of ∆CPD = area of ∆AQD.