Mathematics
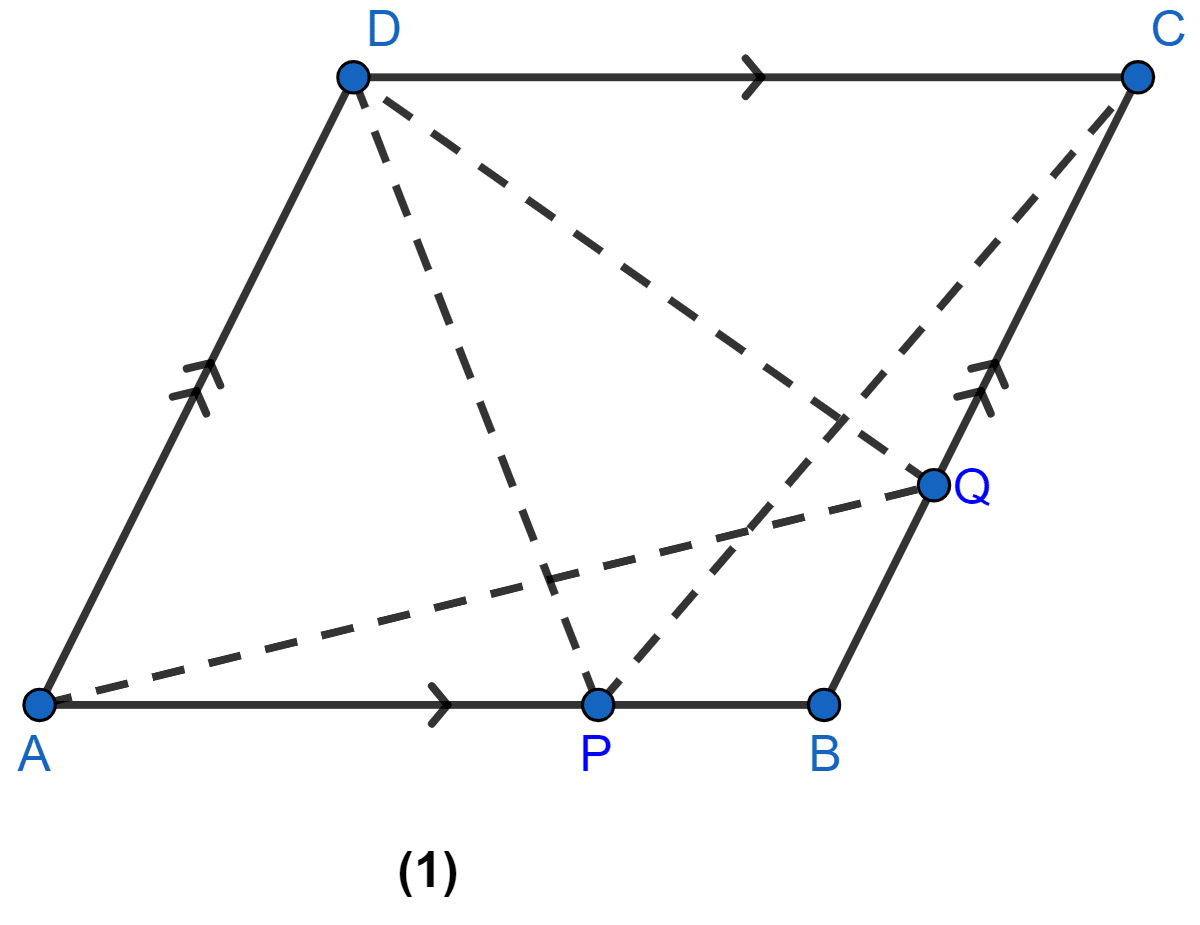
In figure (1) given below, ABCD is a parallelogram. P, Q are any two points on the sides AB and BC respectively. Prove that
area of ∆CPD = area of ∆AQD.
Theorems on Area
15 Likes
Answer
∆CPD and || gm ABCD are on the same base CD and between the same parallel lines AB and CD.
Area of ∆CPD = Area of ||gm ABCD …….(i)
∆AQD and || gm ABCD are on the same base AD and between the same parallel lines AD and BC.
Area of ∆AQD = Area of ||gm ABCD …….(ii)
From (i) and (ii)
Area of ∆CPD = Area of ∆AQD
Hence, proved that area of ∆CPD = area of ∆AQD.
Answered By
11 Likes
Related Questions
If E, F, G and H are mid-points of the sides AB, BC, CD and DA, respectively of a parallelogram ABCD, prove that area of the quad. EFGH = area of || gm ABCD.
In the figure (2) given below, O is any point inside a parallelogram ABCD. Prove that
(i) area of ∆OAB + area of ∆OCD = area of || gm ABCD.
(ii) area of ∆OBC + area of ∆OAD = area of || gm ABCD.
D, E and F are mid-points of the sides BC, CA and AB respectively of a ∆ABC. Prove that
(i) FDCE is a parallelogram
(ii) area of ∆DEF = area of ∆ABC
(iii) area of || gm FDCE = area of ∆ABC
In the figure (2) given below, PQRS and ABRS are parallelograms, and X is any point on the side BR. Show that
area of ∆AXS = area of || gm PQRS.
