Mathematics
D, E and F are mid-points of the sides BC, CA and AB respectively of a ∆ABC. Prove that
(i) FDCE is a parallelogram
(ii) area of ∆DEF = area of ∆ABC
(iii) area of || gm FDCE = area of ∆ABC
Theorems on Area
30 Likes
Answer
∆ABC with D, E and F as mid-points of the sides BC, CA and AB, respectively is shown below:

(i) F and E are midpoints of AB and AC respectively.
So, by mid-point theorem,
FE || BC and FE = BC ………(1)
Also, D is the mid-point of BC
CD = BC …….. (2)
From (1) and (2),
FE || BC and FE = CD
Since, FE || BC so,
FE || CD and FE = CD ……… (3)
Similarly,
D and F are the midpoints of BC and AB.
So, by mid-point theorem,
DF || AC and DF = AC ………(4)
Also, E is the mid-point of AC
EC = AC …….. (5)
From (4) and (5),
DF || AC and DF = EC
Since, DF || AC so,
DF || EC and DF = EC ……… (6)
From 3 and 6,
FE || CD, FE = CD, DF || EC and DF = EC.
Since, opposite sides of FDCE are parallel and equal.
Hence proved FDCE is a parallelogram.
(ii) Since,
BD = CD (As D is mid-point of BC), FE = CD (Proved above) and FE || CD
So, BD = FE and BD || FE.
Hence, BDEF is a || gm.
Since,
FD = EC (Proved above) and AE = EC (As E is mid-point of AC) and FD || EC.
So, FD = AE and FD || AE.
Hence, AFDE is a || gm.
We know that, FDCE is a parallelogram and DE is a diagonal of || gm FDCE.
So, area of ∆DEF = area of ∆DEC (As diagonal divides || gm into two triangles with equal area) ……..(1)
We know that, BDEF is a parallelogram and FD is a diagonal of || gm BDEF.
So, area of ∆DEF = area of ∆FBD (As diagonal divides || gm into two triangles with equal area) ……..(2)
We know that, AFDE is a parallelogram and FE is a diagonal of || gm AFDE.
So, area of ∆DEF = area of ∆AFE (As diagonal divides || gm into two triangles with equal area) ……..(3)
From 1, 2 and 3 we get,
area of ∆DEF = area of ∆DEC = area of ∆FBD = area of ∆AFE ………(4)
From figure,
area of ∆ABC = area of ∆DEF + area of ∆DEC + area of ∆FBD + area of ∆AFE
= area of ∆DEF + area of ∆DEF + area of ∆DEF + area of ∆DEF (From 4)
= 4 x area of ∆DEF.
∴ area of ∆ABC = 4 x area of ∆DEF
⇒ area of ∆DEF = area of ∆ABC
Hence, proved that area of ∆DEF = area of ∆ABC.
(iii) From figure,
Area of || gm FDCE = Area of ∆DEF + Area of ∆DEC
= Area of ∆DEF + Area of ∆DEF (From part (ii) eqn. 4)
= 2 area of ∆DEF
= area of ∆ABC [As area of ∆DEF = area of ∆ABC]
= area of ∆ABC.
Hence, proved that area of || gm FDCE = area of ∆ABC.
Answered By
14 Likes
Related Questions
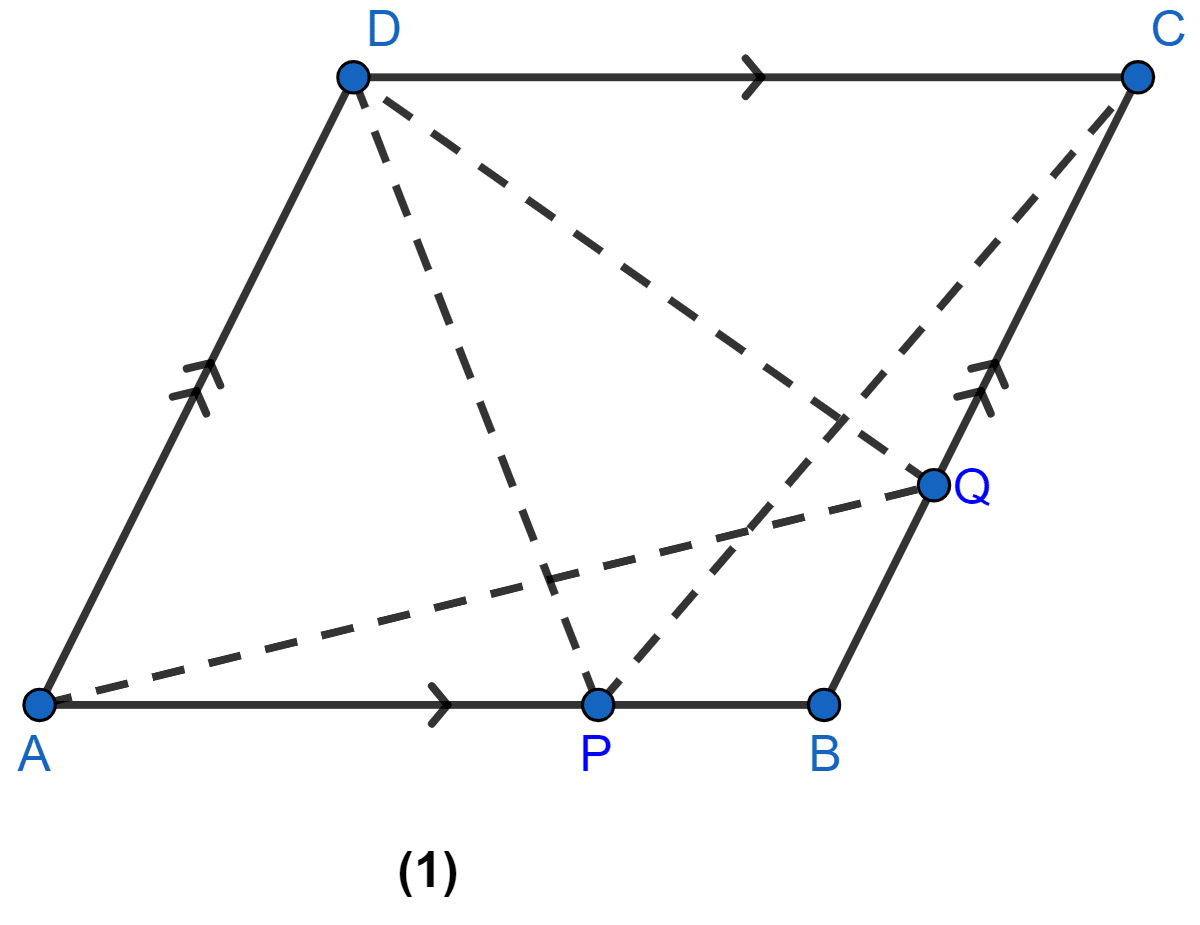
In figure (1) given below, ABCD is a parallelogram. P, Q are any two points on the sides AB and BC respectively. Prove that
area of ∆CPD = area of ∆AQD.
In the figure (2) given below, PQRS and ABRS are parallelograms, and X is any point on the side BR. Show that
area of ∆AXS = area of || gm PQRS.

In the adjoining figure, D, E and F are midpoints of the sides BC, CA and AB respectively of ∆ABC. Prove that BCEF is a trapezium and area of the trap. BCEF = area of ∆ABC.

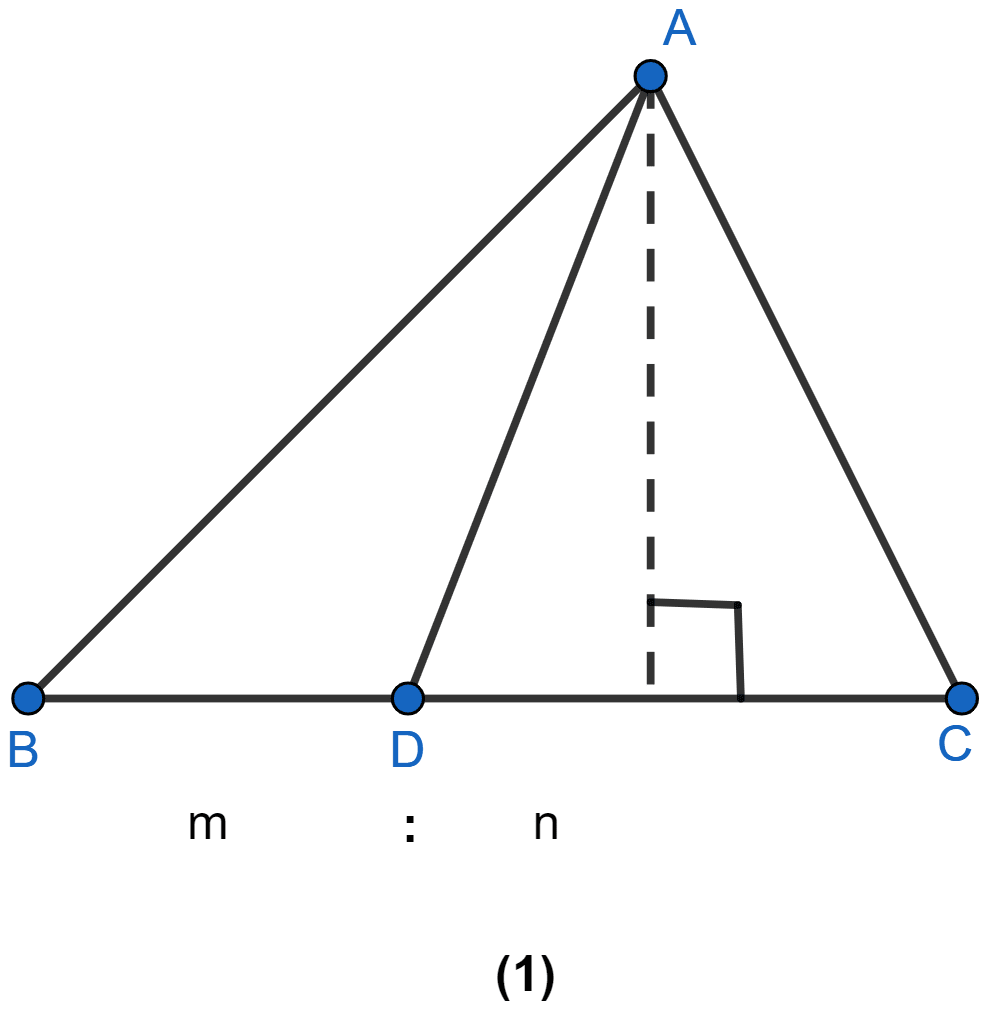
In figure (1) given below, point D divides the side BC of ∆ABC in the ratio m : n. Prove that area of ∆ABD : area of ∆ADC = m : n.