Mathematics
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Answer
In △ABC, AB = AC and a circle with AB as diameter is drawn which intersects the side BC at D.
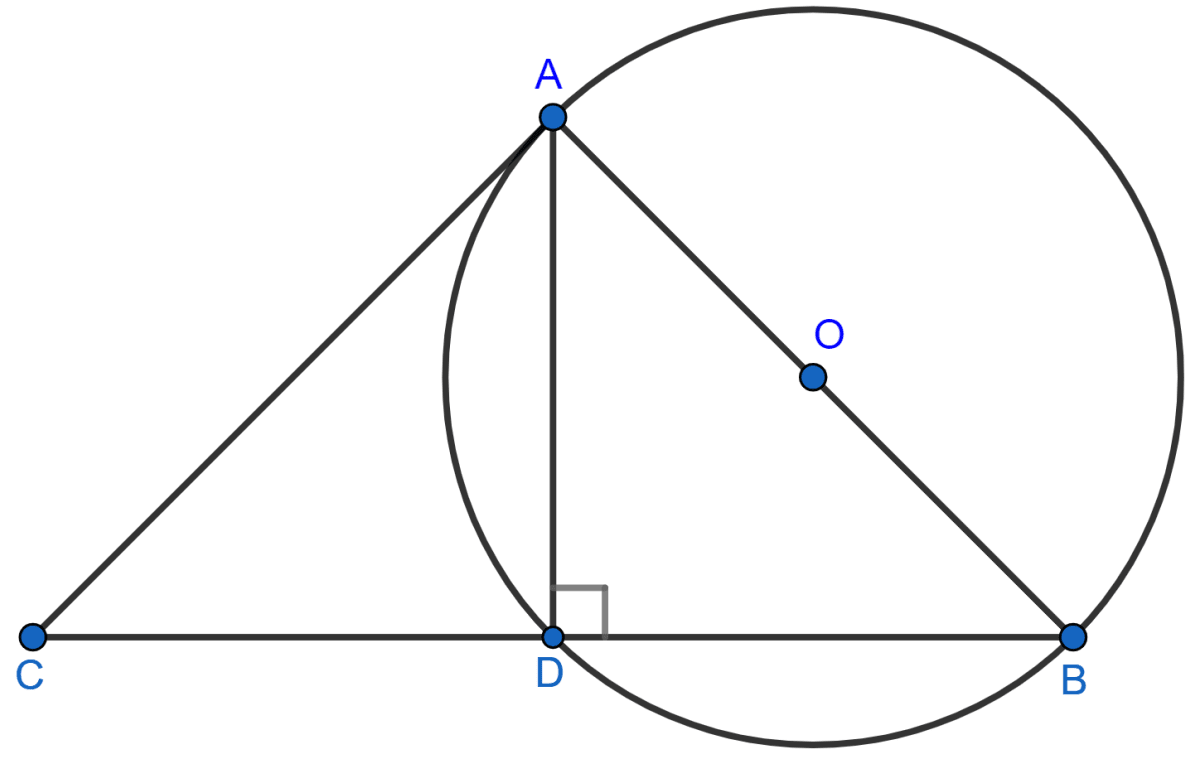
From figure,
∠ADB = 90° [Angle in semi-circle is a right angle.]
Also,
⇒ ∠ADB + ∠ADC = 180° [Linear pair]
⇒ ∠ADC = 180° - ∠ADB
⇒ ∠ADC = 180° - 90° = 90°.
In △ABD and △ACD,
⇒ AB = AC [Given]
⇒ ∠ADB = ∠ADC = 90°
⇒ AD = AD [Common]
∴ △ABD ≅ △ACD by RHS axiom of congruency
∴ BD = CD [By C.P.C.T.]
∴ D is mid-point of BC.
Hence, proved that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Related Questions
In the given circle with diameter AB, find the value of x.

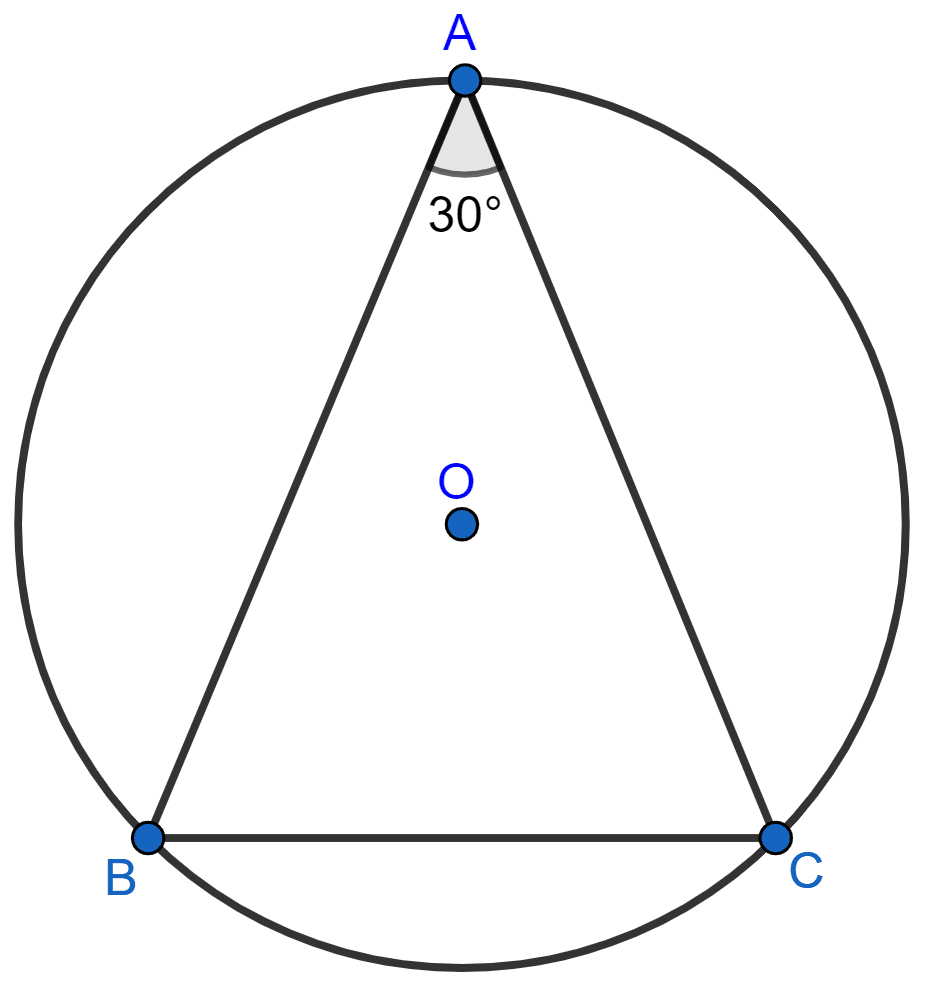
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
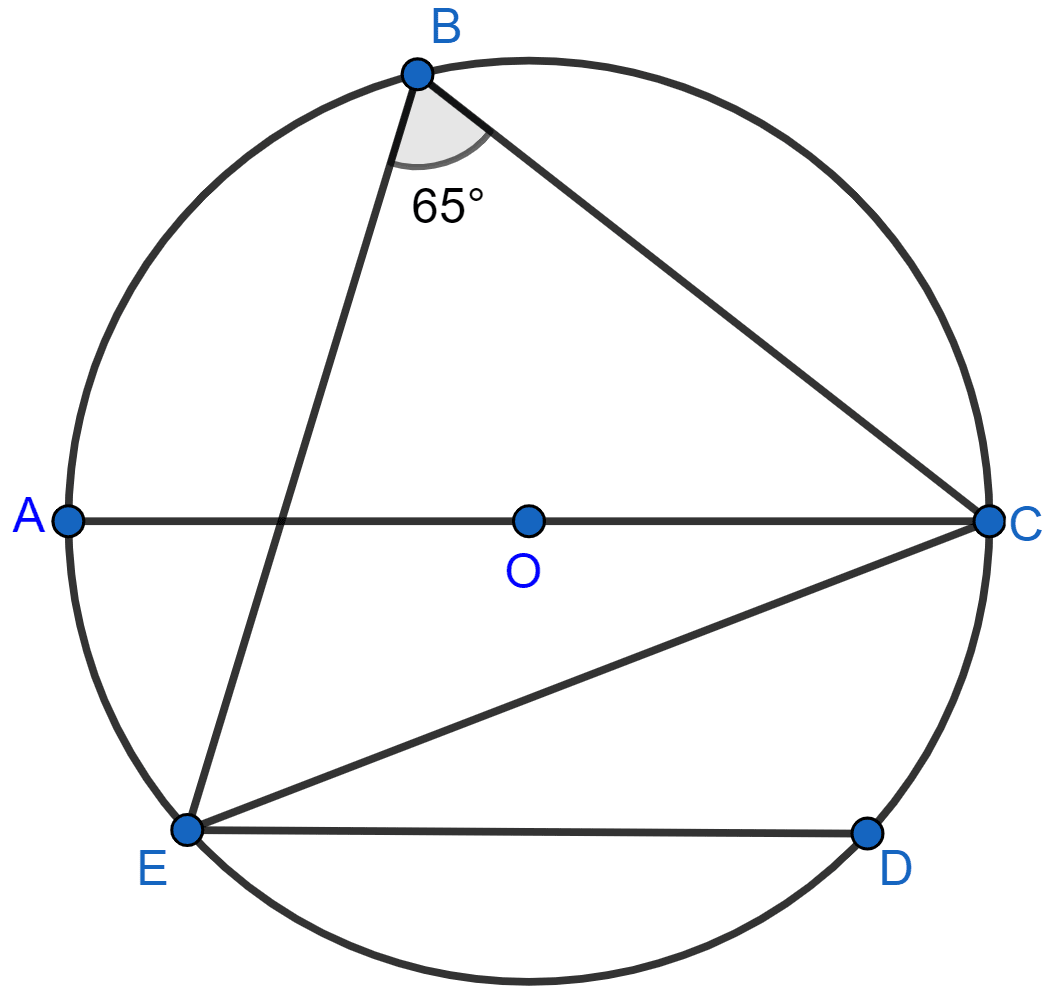
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate :
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC